I gathered a few of the comments made by participants of my lecture “Why quantum computers cannot work and how”, and a few of my answers. Here they are along with some of the lecture’s slides. Here is the link for the full presentation.
1) Getting started
Aram Harrow: Introduces me, mentions our Internet debate and that the day of the lecture was our first meeting in person, mentions that he (still :)) does not agree with me.
2) Special-purpose devices and the “trivial flaw”
(slides 4; 10/11).
Peter Shor: But there are various examples of classically controlled quantum evolutions
Scott Aaronson: So your critique goes only against universal quantum devices and not against computationally superior special-purpose devices? (Answer: no)
3) Topological quantum computing
Why topological quantum computing cannot shortcut the need for ”traditional” quantum fault tolerance (slides 16-18).
Aaronson: Such an argument can be made against every yet unavailable technology.
Mary Beth Ruskai: Agree(?) regarding topological quantum computers, but not that the argument has anything to do with cluster state computation. Several other people expressed the belief that cluster-state computation is not in conflict with my conjectural view of noisy quantum systems.
Shor: Do you disbelieve in the fractional quantum hall effect, then?
(Answer: No, just not in the possibility to create highly stable qubits based on anyons. Mixture of different codewords representing a topological state is OK.)
4) My conjectures 1-4
(slides 29-35):
AM1 (audience member 1): Conjectures 1-3 (but perhaps not 4) are not in conflict with quantum fault-tolerance and the threshold theorem. (Answer: I dont think so; this was discussed in the debate.)
Ruskai: The two-qubit conjecture is too weak to cause QFT to fail. (Answer: indeed I strengthen the conjecture two slides ahead, but I am not sure that we meant the same thing.)
5) Sure/Shor separator
(slide 35):
Aaronson: Constant depth quantum computing still allows certain quantum advantages over classical computing.
Aram: also Shor’s algorithm can be implemented with rapid classical control.
(Answer: we will attend to it in due time 🙂 )
6) Smoothed Lindblad evolutions
And my conjecture that realistic quantum systems are well approximated by smoothed Lindblad evolutions (briefly: SLE). (Slides 36-39.)
Shor: You get something different (by smoothing) when you take time intervals [0,1/2] and [1/2,1]; It makes no sense that the conjecture applies in all scales; You need scales and you need units (I did not get the last point.)
Ruskai: What do you mean by “approximate?” (Answer: excellent question.)
Shor: What about spin echo (NMR)?
(A comment I made in response: actually, Aram raised NMR among several other points “against” SLEs a few days before the lecture; we will have to look at them. Since my smoothing just reorganizes the noise, I expect that it will have little effect for quantum systems that do not enact quantum fault-tolerance.)
AM2: Can you prove that SLE do not support FTQC? (Answer: no) AM2: So what are we talking about here?
Why smoothed Lindblad evolutions are still Lindblad. (Thanks to Robert Alicki.)
7) Causality
(slides 40/1/2)
AM3: My explanation resembles something in classical mechanics which naively appears to contradict causality (the principle of least action, perhaps); Aaronson: Ironically, this causality paradox from classical physics is explained using quantum mechanics. (AM3 made other good comments that I don’t remember.)
8) Simulating physics
(Slides 51/52)
Ruskai : But what does “simulate” mean? (Answer: Excellent question! But if I get to that it will not be a short answer, and probably the “yes” will be modified.)
9) A few additional remarks and questions
Alex Arkhipov: Do my conjectures forbid certain states or only some evolutions (Answer: States are also restricted but this requires the setting of noisy quantum computers: local operations on a Hilbert space with tensor product structure.)
Seth Lloyd: Are there experimentalists in the room? (Apparently not.) The lecture seems remote from what experimentalists care about. Lloyd does not expect mathematical proofs for impossibility of quantum fault-tolerance (answer: neither do I). He is a theoretician much involved with experimental work. In reality, there is all sort of crazy noise (non Lindbladian, even non-completely-positive,) and one should pay attention also to 1/f noise. Overall, he disagrees with me.
Bob Connelly: How sure are you in your conjectures? What is, from 0% to 100%, your level of confidence? (I did not know how to answer this question.)
AM4: Nature does not understand ‘conjectures,’ it just does what it does.
10) Reasons to disbelieve
(Slide 57; based on this post.)
Update (July 2013): The comment thread contains a long interesting discussion with Peter Shor, and Aram Harrow mainly on smoothed Lindblad evolutions, with contributions also by Klas Markström and John Sidles. I added also a couple remarks on further comments I heard while giving a similar lecture at HUJI, and from participants in QStart, and a comment with my 5-minute talk at the rump session in QStart.
Combinatorics and more 
These are excellent comments/questions from Harrow, Shor, Aaronson, Ruskai, Lloyd, Arkhipov, and Connelly! To paraphrase a celebrated speech by US President John Kennedy: “Such an assembly of quantum talent has not been previously been witnessed, with the possible exception of when Hugo Martin Tetrode dined alone!” (see also arXiv:1112.3748).
Thank you Gil, for inspiring everyone to think hard and well regarding these difficult quantum questions.
WIth respect to Aram Harrow’s questions regarding multiple-quantum NMR spin echoes, the appended two articles (out of Warren S. Warren’s group at Princeton) provide an overview of the main theoretical ideas and experimental evidence.
One-sentence summary: Magnetic resonance phenomena that are generically predicted by multiple-quantum coherence dynamics are known not to generically require multiple-quantum coherence dynamics.
—————
@article{Author = {Lee, S and Richter, W and Vathyam, S and Warren, WS}, Journal = {{J. Chem. Phys.}}, Number = {{3}}, Pages = {{874-900}}, Title = {{Quantum treatment of the effects of dipole-dipole interactions in liquid nuclear magnetic resonance}}, Volume = {{105}}, Year = {{1996}}}
@article{Author = {Zhang, H. and Lizitsa, N. and Bryant, R. G. and Warren, W. S.}, Journal = {J. Magn. Reson.}, Month = {Jan}, Number = {1}, Pages = {200–208}, Title = {{{E}xperimental characterization of intermolecular multiple-quantum coherence pumping efficiency in solution {N}{M}{R}}}, Volume = {148}, Year = {2001}}
Thanks, John! We do plan to come back to NMR as a potential counterexample to smoothing the noise in time idea, and also to various others concerns regarding the smoothed Lindblad evolutions.
A few more remarks, John. Indeed there were quite a few other very good questions and comments and one of my problem was that
I could not record many of them while concentrating on my talk. For example, I am not sure if the causality issue raised by AM3 is indeed the least action principle.
One more thing that I certainly need to return to is approximate cluster states, when the approximation is of the nature I expect them: mixture with undesired codewords.
It was left as an open question (I think it was the first open question of the debate)
if such states still support universal quantum computation and I do not know what the answer is.
There was something I was confused about for quite a while and a useful correspondence with Lucas Svec helped me to figure it out. Mathematically, the SLEs are a subclass of all Lindbladians. But my formula and the dependence on the past (and even on the future) looks utterly non-Markovian – so the question was how can my time-smoothing give a subclass of Lindblad evolutions.
I remember that this caused some confusion in the discussion over the blog and also, earlier, in some private discussions. At the end, this conflict of intuitions is based once more on what I refer to as the “trivial flaw”.
Of course, there is no need to stick to Lindbladian noise models when you apply my time-smoothing. (I like the term smoothed Lindblad evolutions because the initials SLE are identical to a famous (unrelated) class of stochastic evolutions introduced by Oded Schramm.)
A simple way to state the conjecture about time-smoothing is that in a realistic quantum system, applying my time-smoothing (for every time scale) gives a good approximation of the original system.
Gil, this “smoothing” program seems reasonable (to me). As for the physical mechanism of smoothing, perhaps that is simply what we call “field theory” …that is, a constraint that Nature forces upon all quantum systems, that they dynamically couple to a vacuum-state continuum. This is a quantum dynamical constraint to which Nature permits no exceptions; one wonders why?
Over on Shtetl Optimized, we see today that some of the energetic ideas that your talk “emitted” are being “absorbed” even by Hilbert-space acolyte Scott Aaronson, who thoughtfully remarks:
(emphasis as in the original).
Perhaps Nature is suggesting to us that the sobering conclusion of the previous decade “scalable quantum computing is far harder than we thought; perhaps even infeasible” has a wonderfully optimistic corollary “quantum simulation is far easier than we though; perhaps even in P.”
To apply a favorite Feynman phrase, that would be terrific!
GK: Unfortunately this good comment and the next one were swallowed by the system until I manage to salvage them many days later. Your comment on coupling to a vacuum-state continuum and connection to field theory is very interesting, John!
Thank you Gil … further remarks by you and Aram (and others) are eagerly anticipated. On Scott Aaronson’s weblog Shtetl Optimized I have posted a link to this “smoothed quantum evolution” discussion together some reasons why this topic (as it appears to me) has both practical and fundamental significance.
Pingback: Special Report: New Quantum Structure of the Universe #OccupyAtlanta #OTB | Censorship in America
One point. Alicki’s formula for smoothed Lindblad evolutions has a term K(t,s) in them which sets the time scale. Your slide didn’t have such a term, and without that term the formula you had on the slide made no sense to me; I don’t see how you can time-smooth on all possible time scales.
Dear Peter, thanks for the remark. My slides had the term
rather than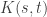 
so it was more restricted, and I talked about a fixed time interval [0,1]. Indeed, before your good comment in my lecture I did not give much thought to the time scale issue.
As my initial reaction to your comment was, I think that for a realistic quantum system described in terms of a Lindblad evolution it is the case that for every time interval (which presecrbes the time scale,) the system can be well-approximated by a smoothed Lindblad evolution. (Both the smoothing and the notion of approximation will depend on the time interval and hence on the time-scale). Less ambitously, we can replace “realistic quantum system” by “a quantum systems that ‘do not invoke’ quantum fault-tolerance.” (As I wrote in a comment above it is not necessary to insist that the noise term is Lindblandian to start with.)
Another way to think about it is as follows. You give me a description of a quantum system that you want to realize in a certain time interval. (It is up to you to make sure that your description is based on “first principles” or that it obeys any other requirement that you regard as important.) I perform a smoothing-in-time on your system and check if the resulting quantum system well-approximates the original one. If the answer is yes I declare your system kosher. And if the answer is no I declare your system non-kosher.
Regarding time-scales and noise, it is also an interesting issue that I try to address how to bound from below the rate of noise for general quantum systems.
But doesn’t the smoothing have to take place along some time scale. If you blur a picture, you can’t blur it on all scales … blurring the picture on the largest scale completely destroys the pixels on the smallest scales, and blurring the picture on the smaller scales leaves the image intact on the largest scales. So how can you smooth a Lindblad evolution on all scales?
Peter, The smoothing is done with respect to a single time interval and thus with respect to a single time scale. (Or, more precisely, one time-scale at a time.) The conjecture is that the quantum system is well approximated by a smoothed one, or even by its own smoothing. If you shift your attention to a smaller time interval then you have to adjust both your smoothing kernel and your notion of approximation. (But the conjecture should still hold.)
Actually your example about blurring pictures is very good. Suppose that you conjecture that if you blur a “natural” photo it well approximates the original. You can consider this conjecture for this picture (lets call it picture 1), and then the blurring is done w.r.t. length-scale of that picture. You can also consider this picture (picture 2) and then the blurring is w.r.t. the length scale of picture 2. Actually picture 1 is a tiny window inside picture 2 and indeed when you blur picture 2 the details of the little window of picture 1 may disappear, but this will be taken into account by your approxmation-measure. (See this post where these pictures come from; it would be great to take some similar pictures with you 🙂 soon.)
In this case, pictures like this one or this one will probably fail the blurring condition. The mathematical property of “blurring is a good approximation” makes an interesting distinction that our vision and image processing friends are surely aware of.
I am quite interested in studying quantum processes where my smoothing is a good approximation. One other thought invoked by your comment about scales is that fractalish behavior is a multi-scale property.
My question is then: how does the quantum system know whether it is doing a quantum computation on time scale t1 or on time scale t2?
Dear Peter, consider a quantum system running on a huge Hilbert space for a long time. We choose a window: a small Hilbert subspace and a small interval of time. The conjecture is that for this window the smoothed evolution will be a good approximation for the evolution without smoothing. Of course, the system “does not know” our choice of the window.
So let me see if I have it straight. I don’t believe that Nature can actually follow the equation for smoothed Lindblad evolution that you wrote down, because the K(t-s) term would have to depend on the time window that you’re looking at. But you think there is some similar kind of smoothing which happens on multiple time scales, so that whatever time scale you look at, you lose enough resolution to foil quantum computation but not enough resolution that it would have been distinguishable by experiment from the predictions of un-noisy quantum mechanics.
” I don’t believe that Nature can actually follow the equation for smoothed Lindblad evolution that you wrote down, because the K(t-s) term would have to depend on the time window that you’re looking at. But you think there is some similar kind of smoothing which happens on multiple time scales,”
This is an excellent point that need to be clarified. I also do not believe that any smoothing is “happening.” The smoothing is not a physical process that mixes at present the noise from the past and from the future. The smoothing is a mathematical tool to describe the systematic connection between the quantum system, the device that realizes the quantum system, and the noise model. This is related to what I referred to in my talk as the “trivial flaw”. We do not have a single device capable of doing everything but we may need special devices for different tasks.
The way nature can follow my smoothing equation is this: The systematic relation between evolution-device-noise excludes those quantum systems which violate it. Again, no actual “smoothing” is happening at any scale.
So what kind of physical process actually is going on? Or do you not have any candidates?
“So what kind of physical process actually is going on? Or do you not have any candidates?”
This is again a wonderful question and here is the way I see it. Noisy quantum computers represent a level of abstraction which is not detailed enough to describe the kind of physical process that is actually going on. For that you need a much more specific physical scenario and a much more detailed modeling. But here comes the beautiful part: this high level of abstraction is nevertheless suitable to describe what actually is not going on. And what is not going on is quantum fault-tolerance.
(Since you started quantum fault-tolerance, this is not such a bad deal 🙂 )
The smoothing is offered as a formal way of saying that quantum fault-tolerance is not going on. In the debate with Aram, and my papers, I offered a few thoughts regarding the kind of physical processes which are actually going on in a few very specific implementations of quantum computation.
So your argument, boiled down, is that there is some kind of noise that interferes with quantum computation. This noise vaguely resembles another kind of noise, but it actually isn’t that noise and doesn’t behave exactly like that noise (e.g., it acts on every timescale, in particular, which smoothed Lindblad evolution doesn’t). We don’t know what is causing this kind of noise. And this kind of noise pops up out of nowhere any time you try to do a quantum computation and ruins it, but it doesn’t ruin similar phenomena which aren’t quantum computations (like the fractional quantum Hall effect).
At this point, I find this theory too vague to even try to refute.
That is a good question, whose implications (as I appreciate them) direct us toward geometric smoothing (a.k.a. “California” pullback) as more natural than temporal smoothing.
In consequence of an episode in mathematico-literary history that is recounted on Schroedinger’s Rat, perhaps Lindblad-smoothing-by-pullback might be called pieuvre dynamics, in token of the inexorably entangling tentacles of polynomial-rank product-state (Segre/secant) manifolds?
Pingback: Mittag-Leffler Institute and Yale, Winter 2005; Test your intuition: Who Played the Piano? | Combinatorics and more
Dear Peter, thank you for your very clear summary of your point of view. My own, different, take on the matter is given in my earlier comments above (and in my lecture). I do plan to try to think about and relate specifically to some of the points you have raised.
Dear Gil, if you can find a way to make your noise model more detailed, I’ll be happy to look at it again.
Peter, one detail I certainly agree that I need to supply is the formal meaning of “approximate” in the conjecture that realistic quantum systems are well approximated by smoothed Lindblad evolutions. Beth asked about it, I completely agree that this is crucial, and I think that filling this missing piece is doable. However, it looks to me that when you say “more detailed” you mean much more that that, right?
Some kind of formula would work. I realize you have a formula for smoothed Lindblad evolution, but it depends on the timescale, and I am not buying a noise formula which depends on the timescale because Nature doesn’t know how long the quantum computation will take in advance. In fact, I suspect that it is impossible for a noise model to behave the way you want it to behave (smoothing it at every timescale, but never blurring it completely). If you can show that there is a noise model which gives multiscale smoothing, that would be great.
Dear Peter,
Briefly, I think that the main difference between our points of view is that you expect me to provide an explicit description for the class of noisy evolutions that I regard realistic (e.g. the class of smoothed Lindblad evolutions) . I am satisfied (and I think you should be satisfied too) with a definition of such a class by an implicit condition like the following: a Lindblad evolution is realistic only if it is well-approximated by a smoothed Lindblad evolution. (Or stronger, by its own “smoothing-in-time.”) I do not think that your interesting critique regarding time-scales applies here. Given a time scale you can dismiss a large number of evolutions as unrealistic, but you do not need to apply the smoothing itself on every time-scale.
Gil: I am amazed that you don’t think the time scale critique is applicable. Suppose we have a system, and when we first look at the evolution of the system from time 0 to time 1000, and we then zoom in and look at it from time 0 to time 1, we find that these two evolutions are incompatible. Are you saying that you don’t find anything wrong with that?
I’m not saying that smoothed Lindblad evolution on multiple timescales is impossible. But my intuition says that it shouldn’t work. And if it doesn’t, I am not satisfied.
Peter, the crucial point is that I refer to approximation. Think about the notion of “well-approximated” as expressing, in the case of noisy quantum computer, an expected gap, along the evolution (between the state of the system and its approximation), of
qubits where 
, say. It is possible for a quantum evolution to be well approximated by a smoothd Lindblad evolution for every time scale. The conjecture is that every realistic quantum evolution satisfies this property. The property of being well-approximated by SLE for every time scale do satisfy your compatibility requirement!
Gil, perhaps Peter’s concern is that this might be like that class of functions which has the “stronger-than-Lipschitz” property, i.e.
for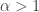 
.
You can prove all sorts of great things about such functions, but then you run into trouble when you try to find an example.
Dear Aram,
My conjecture is:
(*) A quantum system described by a Lindblad evolution is realistic only if it is well-approximated by a smoothed Lindblad evolution (for every time-window).
A somewhat stronger version is
(**) A quantum system is realistic only if it is well-approximated by its own smoothing-in-time. (Again, for every time window).
My smoothing operation depends on the time-window and hence on the time-scale. But the classes of quantum systems described by (*) or (**) do satisfy the time-scale compatibility requirement of Peter. You do not need to create a multi-scale version of smoothed Lindblad evolutions for this purpose. There is more to be said on the issue of multiple scales and noisy quantum evolutions, but indeed perhaps it will be useful for me to understand what precisely are Peter’s concerns at this time, and if Peter finds my last comment (that I largely repeat here) as a satisfactory answer to his earlier comment starting with “Gil I am amazed that… .”.
(Regarding your comment, Aram. If you refer to conditions (*) or (**) then they pose severe restrictions on noisy quantum systems but leave alive plenty of quantum systems. If you refer to a hypothetical multi-scale version of SLE that Peter talked about, then, as I explained, this is not needed.)
Gil,
What I am worried about is that you require that the evolution of the system from time 0 to 1000 be smoothed on a time scale of 1000. But my intuition tells me that any valid evolution of a system from time 0 to 1 should be the start of some (in fact, of many) valid evolutions of the system from time 0 to 1000. Can you show that this is true of smoothed Lindblad evolution, given that you are requiring that the evolution of a system from time 0 to 1 only be smoothed on a time scale of 1? Or do you disagree with my intuition?
Hi Peter,
“What I am worried about is that you require that the evolution of the system from time 0 to 1000 be smoothed on a time scale of 1000.”
Approximately smoothed
“But my intuition tells me that any valid evolution of a system from time 0 to 1 should be the start of some (in fact, of many) valid evolutions of the system from time 0 to 1000.”
Peter, we can come back to this intuition, but let’s take it for granted that you can add the identity as the unitary part (with your favorite description for the noise) from time 1 to time 1000. (Or does your intuition goes further than that?)
“Can you show that this is true of smoothed Lindblad evolution, given that you are requiring that the evolution of a system from time 0 to 1 only be smoothed on a time scale of 1?”
If you take
anyan evolution on time [0,1], which is approximately smoothed on a time scale 1, and add to it the identity as your unitary part from time 1 to time 1000, then the system from time 0 to 1000 will also be approximately smoothed.(I think that the issues of time scales as well as your intuition from the last comment are interesting and deserve further discussion, but let me try first to clarify the more technical matters. )
Pingback: Special Report: New Quantum Structure of the Universe #OccupyAtlanta #OTB | Michael Florin
Hi Gil,
Can you explain how your statement works:
If you take any an evolution on time [0,1], which is approximately smoothed on a time scale 1, and add to it the identity as your unitary part from time 1 to time 1000, then the system from time 0 to 1000 will also be approximately smoothed.
To get the smoothing on a time scale of 1000 from time 0 to 1, don’t you have to convolute the noise operator E_s with K(s,t). Isn’t that going to give you a \tilde{E}_s which is different from your original E_s?
Dear Peter, my intuition is the following: If the unitary part of the evolution is the identity, then smoothing will make no difference as the system before smoothing is identical to the system after smoothing. If the unitary part of the evolution is the identity for the last 99.9% of the time, then smoothing should make a little difference since for most times the noise term after smoothing is very close to the noise term before smoothing. (The precise notion of distance between two Lindblad evolutions should be chosen to make this intution works, but it looks quite reasonable.)
If \tilde{E}_s is different but very close on average to my original E_s, then I regard the original E_s “approximately smoothed”.
For that to be correct, wouldn’t E have to be the identity whenever the unitary part of the evolution is also the identity. In other words, isn’t this assuming perfect quantum memory? If E_s isn’t the identity when the unitary part of the evolution is the identity, then won’t the noise the system accumulates between times 1 and 1000 when it is undergoing no evolution have to be transformed back through U_s,t and become some very entangled noise on the system between times 0 and 1? Or am I misunderstanding your smoothed Lindblad evolution equation?
Yes, the situation in time [0,1] can be hairy. But I take the average of the distance between \tilde{E}_s and E_s over all times between 0 and 1000. Whatever happens between time 0 and 1 can make only a very small difference. (In fact, I think that you do not even need to assume that the evolution is approximately smoothed in the interval [0,1].)
GIl,
Then make it between 1 and 10, or 1 and 2, and not between 1 and 1000.
Peter, I don’t think your revised argument is harmful to what I am saying.
The ball park for realistic quantum evolutions are those evolutions which are well approximated (for every time window) by smoothed evolutions. The precise dependence of the approximation on the kernel used for smoothing (or just on how concentrated the kernel is) can be a factor in telling how hard it is to realize a specific noisy evolution. And somewhere in this ball park will be the border between what we can achieve and what we cannot achieve. (Quantum algorithms involving quantum fault tolerance are, I think, way out of this ball-park.)
Now, you start with a realistic noisy evolution which runs in the time interval [0,1] and at the end create a certain quantum state. Your intuition is that if we want to maintain the end-state for the time interval [1,2] or even [1,10] this new task is still in the realistic ball park. This seems correct, but since the new task is harder, the precise kernel we should take may be different.
(With your [0,1]- [1,1000] earlier version there was a possibility that something that is only somewhat harder gets asymptotically out of my ball-park altogether. But it turned out that this is not the case.)
Hi Gil,
I guess I don’t really understand your SLE theory. Maybe you could illustrate what happens on a simple example. Take a qubit. Put it in state |0⟩. Now subject it to noise with a weak depolarizing component and a strong dephasing component. Wait long enough until it is only slightly depolarized and very dephased. Rotate it by a small angle θ. Wait for the same amount of time. Then measure it.
I know what quantum mechanics predicts for the outcome. What does your theory predict will happen. If it is the same as quantum mechanics, why?
Peter,
I too have been trying to understand Gill’s conjectures so I’ll take the liberty to say what I think Gill would reply here, and then Gill can tell me if I have understood him or not.
I believe that Gill claims that it is not possible to build a universal quantum computer and instead one will have to build a physical machine for the specific purpose of performing the computation in your example. This machine will not only define the computational process but it’s physical properties will, in a self-referential way, also determine the structure of the noise and because of this the noise will have properties that ruin any quantum error correcting codes one wishes to use.
If this is the case then it is impossible to separate the noise on computational process from it’s physical implementation, so this takes the claim outside mathematics and makes it a “physics conjecture” instead.
Does this agree with what you are saying Gill?
Hi Klas,
This may describe Gil’s philosophy in general, but I’m looking for something much more specific: the application of the SLE conjecture to this problem. It seems to me that there are one of three possibilities. (a) Gil predicts that the evolution of this system is not that predicted by standard quantum mechanics. (b) Gil can show that there is a smoothed Lindblad operator which approximates the evolution of this system. (c) I completely misunderstand what Gil is saying.
Dear Peter and Klas,
1) Indeed Klas’s comment is a good description on my point of view. Thanks, Klas.
2) Peter’s comment is a good opportunity to clarify a few things.
Peter: “I know what quantum mechanics predicts for the outcome. What does your theory predict will happen. If it is the same as quantum mechanics, why?”
It goes without saying that for every quantum system my predictions are precisely as those as quantum mechanics. The SLE is a proposed tool for telling if a quantum system is realistic, or more neutrally, if a quantum system enact quantum fault-tolerance. (Thus, my smoothed quantum systems form a subclass of general quantum systems, and I think that they can give a good description of realistic noisy quantum evolutions.)
In cases that the quantum system is not fully specified e.g. when only the unitary part is described or only a pure target state is specified then my conjectures indeed give predictions about how a realistic quantum system meeting these partial specifications will behave. For example, one of the conjectures refers to how noisy approximations of codewords in a quantum code will behave.
3) Peter: “It seems to me that there are one of three possibilities. (a) Gil predicts that the evolution of this system is not that predicted by standard quantum mechanics. (b) [Gil can show that] there is a smoothed Lindblad operator which approximates the evolution of this system. (c) I completely misunderstand what Gil is saying.”
It looks completely obvious to me that (b) applies here. (Since this does not seem to be obvious to Peter maybe there is also some misunderstanding left.)
More generally, if you consider all quantum systems with an absolute bound D on their depth then I think that you can find a fixed Kernel for which the SLE will be a good approximation. You can make sure that most of the mass of K(x) is in a window of length (ε/D).
4) About time scales. I think that we clarified the specific concerns regarding time-scaling and smoothing but there are interesting issues left to be discussed regarding time-scales and realistic noisy quantum evolutions.
Okay, if (b) is the case, what is the smoothed Lindblad operator which approximates the evolution of the system.
Just the smoothing of the system as you described…isn’t it?
Hi Gil,
If you have two sources of dephasing noise at an angle θ, they generate depolarizing noise which (for ε large enough) gives a different physical outcome than pure dephasing noise. Here, ε needs to depend on the intensity of the dephasing noise, so fast dephasing drives the possible ε you can use towards 0.
Let’s try to figure out our differences for this nice example. The unitary evolution consists of a single gate which rotates the qubit at angle θ. We consider two equal time intervals before and after the rotation. We start with a certain noise at each time E_t and then apply smoothing with respect to a parameter ε. I claim that the average distance between \tilde{E}_s and E_s is small when ε is. (Uniformly for all choices of the starting noise E_t’s) You claim that depending on the nature of the noise itself we may need to take ε to zero. Is this a correct description of our disagreement on this example?
There’s a time constant associated with dephasing noise, I think that the parameter ε has to scale proportionately to the time constant. But lets take the time constant to be roughly the length of a single gate. You can then think of this computation as applying n/2 identity gates, one gate which rotates by an angle θ, and then another n/2 identity gates. I think that you are not going to get reasonable results unless you only smooth over a constant number of gates, and not over εn gates.
In my smoothing ε is always proportional to the time interval. If you wish to consider the time interval as divided to n/2 identity gates then the rotation and then additional n/2 identity gates (I dont understand why to look at it this way) then the smooting scale in terms of number of gates will be indeed εn. (Still it looks to me that on average \tilde{E}_s and E_s will be very close.)
Hi Gil,
Maybe I made my comment too quickly. What is ε? I didn’t realize that your conjecture allowed you to choose ε. If you are allowed to choose ε arbitrarily, then isn’t your SLE conjecture trivially true? If you’re not allowed to choose ε arbitrarily, what is the reason that you think that your conjecture works for ε = 1/1000, but not for ε = 1/3?
Furthermore, if you keep making ε small enough to allow for all physics experiments done to date, aren’t we chasing a moving target?
Hi Peter, There are two parameters which we need to choose (or to relate) one is how well (on average) \tilde{E}_s approximates E_s and the other is what is the kernel and here perhaps we can think about the kernel as a truncated Gaussian and just refer to its variance. I think that for quantum processes with quantum fault tolerance, \tilde E_s and E_s will be utterly unrelated even when ε is tiny. I would expect E_s and \tilde E_s to have good correlation for realistic cases (like the one you suggested) even for pretty large ε, say ε=1/3.
It seems that “morally” the SLE conjecture is closely related to quantum computing having bounded depth (sort of the early Unruhian approach). Of course, one may argue that if this depth D is a million then this not only accounts for all physics experiments done to date but may also allow some interesting fault tolerance computing. (This is the moving target flavour of any asymptotic claim.) Actually I expect that once you set your realistic ball park in terms of these SLE or the depth D the border line will be more in the neighborhood of D=3 rather than a million.
Hi GIl,
I don’t see how you can make this work by choosing ε small enough.
What keeps me from making a “quantum computation” which has two parts: one is my little experiment above, repeated every time step (maybe many copies repeated each time step). To do this, all you should need is to get a quantum computer to remember classical information, and if smoothed Lindblad evolution can’t remember classical information, there is something really wrong with it (since actual computers can). The other part is a true quantum computation that factors a large number. Maybe you could show that if ε is small enough that most of the time my little experiment works as it should, then ε is small enough for the actual quantum computation to work.
Hi Gil:
I think I can go back to the heart of my problem with smoothed Lindblad evolution. This was actually the intuition behind my first objection, but it’s much better clarified in my mind now. Suppose I apply some quantum gates to a quantum system. If we view the computation as taking place between times 0 to 1, you smooth using one kernel. If we view the computation as taking place between times −10 to 10, the kernel gets scaled, and we effectively have to smooth using a different kernel.
How does nature know which kernel to use???
You’ve said that it doesn’t matter, because the computation has to be smoothed at all time scales. However, if we use a kernel with too small an ε, quantum computing works perfectly, and if we use a kernel with too large an ε, we can’t match the actual predictions of standard quantum mechanics. So the time scale really does matter: we need to choose the correct ε.
My belief is that smoothed Lindblad evolution cannot work unless the smoothing mechanism somehow depends on some property of the system which tells whether a real quantum computation is or is not taking place.
One small thing about your earlier discusison: I am a little confused about epsilon. Is this the window over which we smooth? If so, what are the units? I would imagine that the units would be in terms of gate speed, so a width-10 window would mean that we average over ~10 gates. But you guys are talking about things like epsilon = 1/3.
Gil, I think Peter’s example is a nice illustration of the point that the behavior of a system depends on how many identity gates we apply. This seems not very plausible.
There is also a classical version of Peter’s argument. Suppose that we have two bits, A and B. A is noisy, and B is not. So there is a noise process that flips A according to a Poisson process with time scale 1 second. B gets flipped rarely, let’s say once a day. (Such a separation of timescales in interacting systems is physically common, e.g. if A is a nuclear spin and B is an electron spin.)
Let’s say the smoothing timescale is 1 second. Then it’s basically irrelevant.
Let’s say it’s 100 seconds. Suppose we do a single swap gate between A and B. It is physically reasonable that for that moment, B, having briefly stuck its hands in the oven, would be subject to higher rates of noise. But smoothing would say that for the next 100 seconds, B experiences noise at a rate of ~1/second. I think most people would consider this an example of a mistaken theory. Worse are the following two additional features of SLE:
1. According to the principle that the smoothing kernel is symmetric in time, B should also experience higher rates of noise for 100 seconds BEFORE the swap gate.
2. The claim is that the noise is described equally well by smoothing at timescales of 1 second, 10 seconds, 100 seconds, 1000 seconds, etc., which even in this extremely simple case I can’t even figure out a mathematically consistent way to describe.
Of course for smoothing to be interesting, it should generate different predictions than “no smoothing” would. But the above scenario, like the one that Peter described, the predictions do not appear to resemble the world we live in.
A small correction: In my example, I had the nuclear and electron spins backwards. The electron spin should be A, and the nuclear spin should be B.
Peter’s two most recent comments (A, B) raised excellent issues and so are some of the “follow-up” points by Aram. So I will be happy to think about them and discuss them further. There are still three minor points which may represent some misunderstanding that are better clarified first.
1) Aram: “One small thing about your earlier discussion: I am a little confused about epsilon. Is this the window over which we smooth? If so, what are the units? I would imagine that the units would be in terms of gate speed, so a width-10 window would mean that we average over ~10 gates. But you guys are talking about things like epsilon = 1/3.”
Aram, We fix a time interval and the smoothing parameter ε is always given in terms of the length of this interval. (In my setting there is no reference to “gates” and I do not see a reason to talk about gates in this context.)
2) Aram: “The claim is that the noise is described equally well by smoothing at timescales of 1 second, 10 seconds, 100 seconds, 1000 seconds, etc., which even in this extremely simple case I can’t even figure out a mathematically consistent way to describe.”
This is not the claim. The claim is that for every time interval the system is described well (in this time interval) by a smoothed system. Of course, there is no claim that if you fix a time interval then smoothing in different time scales are similar. (See e.g. this comment.)
So if you consider a 5 second window then a 1 second smoothing will give you a good picture, and if you consider a 50 second window then a 10 second smoothing will give you a good picture, and if you consider a 500 second window then a 100 second smoothing will give you a good picture, and if you consider a 5000 second window then a 1000 second smoothing will give you a good picture.
3) Peter considered a scenario where we have a quantum system in the time interval [0,1] subject to a certain noise, and to a single (non-trivial) gate of rotation at time 1/2. (we discussed it back and force ending with my last comment here.) I still think that for this example the ε-smoothing will be a good approximation. (Remember, the quality of the approximation is given in terms of how far
and 
are on average. )
Gil: I am confused about this dependence on the window size that we consider. What if 100 people are observing the same system, and each considers a different window size? Similarly for what you said about “fix a time interval” and then have the smoothing window be a fraction of that time interval.
Here is the picture that I have of a classical system (or a quantum system that is periodically measured). I think of it like a a videotape. We can have a 30-frame-per-second record of what is going on and we can review as much or as little of it a we like. It is a function of time, defined as long as the system exists. t is time, and f(t) is the state of the system. It is not f([t_1, t_2]); i.e. not a function of an interval. I don’t know how to make something a function of an interval, other than in a trivial way, i.e. f([t_1, t_2]) is the restriction of f to the domain [t_1, t_2]. But in that case, it is not mathematically well-defined for the amount of smoothing to depend on the length of the interval. More precisely, if I have intervals [t_1, t_2] and [t_3, t_4] which overlap, then f([t_1, t_2]) and f([t_3, t_4]) should be consistent on their intersection.
I guess your answer will be that a single time-evolution will simultaneously appear smoothed on all time scales. This seems to me contradicted by Peter’s example, or my example, or indeed any nontrivial example.
Aram, Peter’s example was the following: you have a time interval [-T,T], noise E_t=E for t in the interval (which was specified but it does not matter), and at time 0 you apply a single unitary U.
When you apply smoothing at time scale εT then when t is not in [- 3εT,3εT] (say), \tilde{E}_s and E_s will be very close together and therefore also on average over T \tilde{E}_s and E_s will be quite close. This is true uniformly when you consider all other time interval [-S_1,S_2] and apply the smoothing proportional to the length of the interval.
As a side note, I don’t think that the right distance measure is whether E_s and tilde{E}_s are close “on average”. The right distance measure is something like the variational distance on the transcript. In both Peter’s example and mine (and indeed for any nontrivial example), the transcripts will look very different, and this will be observable.
But what you wrote about Peter’s example already contains the idea of “smoothing with time scale epsilon T”. The point is that observable quantities depend on this timescale T. But where does T come from? At noon (=time 0), I apply the gate U. At 12:01pm I look at the system. At 12:05pm I look at the system. At 1:30pm I look at the system. This is what experiments look like. There is no single “interval” [-T, T] relative to which the physics is defined.
The purpose of the time smoothing is to make a mathematical distinction between quantum systems that involve quantum fault-tolerance and those that do not. The (mathematical) test is that for every time interval [a,b] when we smooth using a scale proportional to the length of the interval (so the smoothing parameter is ε(a-b)), then the smoothed system is close to the original system in the measure that I specified. So by my criterion Peter’s example pass the test of “not enacting quantum fault-tolerance” which is intuitively very reasonable.
Based on this test, I propose to consider the smoothed Lindblad evolutions themselves as useful models for approximatly-unitary evolutions. (I referred to those as “approximately-pure” in the lecture (and earlier), but Mary-Beth pointed out that this was an ackward terminology.) I agree with some of the points that Peter made regarding this and I will comment on it separately.
I don’t understand the idea of distinguishing between systems that implement FT and those that don’t. Could you distinguish between an algorithm that uses quicksort and one that doesn’t? I think the answer to both is clearly “yes, in some cases, but certainly not in all cases.”
But also I don’t understand the status of SLE. The consensus picture of quantum noise is that there is a Hamiltonian with terms for the system, the environment, and then terms coupling them. Tracing out the environment gives us some effective noisy evolution on the system. Assuming the environment is rapidly mixing yields the Lindblad formalism. Is the content of the SLE conjecture that some part of that picture is wrong? Or should be modified? Under what conditions? “When implementing FTQC” is not really a mathematically well-defined condition. Nor is “when considering an interval of length T”.
I understand that you want to look at the distance measure which measures the average distance been Lindblad operators when averaged over a time T. However, I am not interested in that measure. I am interested in physically observable differences, such as (in my example) the rate at which the bit B flips, or (in Peter’s example) the direction of the spin at the end of the experiment. If such observable differences depend on an ill-defined parameter, such as “the length of the interval that we consider” then I view the theory as ill-defined.
Hi Arram,
“I don’t understand the idea of distinguishing between systems that implement FT and those that don’t. ”
My impression is that Gil does not believe that any computational model which allows fast factoring of integers is realistic, see slide 57 or point 10 above. Since FT allows us to do this he want to find a mechanism which invalidates FT in realistic systems. So in part this is reasoning going backwards from the process he wants to exclude, ie factoring, in order to find some general principle which will exclude it.
But since there is no direct derivation of this from the physics of the system, only the general idea for an effective theory in terms of SLE, the conjectures makes very few concrete numerical predictions which one could use to refute them.
“Tracing out the environment gives us some effective noisy evolution on the system. ”
As I have understood Gil the idea is that the environment can’t be traced out in a way which leaves a simple noise model. He claims that the physical machine which implements the quantum computation will contribute in an essential and self-defeating way to the noise, so the noise will be unique for every computational process and physical implementation of it.
Too me the arguments in favor of the conjecture look much too vague, I would like to see a complete derivation in even some simple concrete situation first, but of course it would be even nicer to get a mathematical argument which shows that the effective SLE theory can be ruled out.
Aram, I propose a formal distinction between realistic (approximately unitary) quantum systems and non-realistic such quantum systems. A system that for some time scale cannot be approximated by smooth-in-time system (for smoothing in the same time scale) is not realistic. And I specify the notion of approximation. So you can regard this proposal like my old conjecture C. If you can exhibit a counterexample this will kill this proposal, like your example with Steve killed my old Conjecture C.
Peter’s example is interesting, but it is not a counterexample to my proposal. Your comment on measuring the distance is interesting, but, again, not directly relevant. My proposal is the main technical issue of this thread, and I think that we have an interesting discussion and I will certainly be happy to see ideas for a counterexample.
Indeed there are also interesting related conceptual issues.
“The consensus picture of quantum noise is that there is a Hamiltonian with terms for the system, the environment, and then terms coupling them. Tracing out the environment gives us some effective noisy evolution on the system. ”
This is an excellent point. What is missing from your description is the device realizing the system. The formal description of the environment can be a function of the device and thus can systematically depend on the evolution. In my talk I referred to ignoring this issue as the “trivial flaw”. (See also Klas’ two comments above.)
“I don’t understand the idea of distinguishing between systems that implement FT and those that don’t. Could you distinguish between an algorithm that uses quicksort and one that doesn’t?”
Understanding when an algorithmic task requires SORTING can be a very important issue and is crucial in understanding when we can hope for linear-time (or very-nearly linear time) algorithms. Let me remind you, Aram, the analogy you made right at the beginning of your argument in our debate between fault-tolerance quantum computing and 3-SAT. It is certainly a central issue to understand which algorithmic tasks require 3-SAT. I think that understanding quantum systems that embody quantum fault tolerance is important, but, In any case my distinction was the motivation for my proposition regarding smoothed evolutions and you don’t need to buy it.
(A minor point regarding Klas’ comment. For me the other reasons to doubt QC, and, in particular, the fact that QCs represent entirely new physical reality are stronger than factoring. Regardless of what you believe about factoring you will certainly check very very carefully and skeptically any specific attempt/approach for a factoring algorithm.)
I really think my example shows that even the simplest systems cannot follow Gil’s idea of smoothed Lindblad evolution hypothesis while still matching the standard predictions of quantum mechanics. The executive summary is that if you simultaneously apply dephasing noise at angle 0 and dephasing noise at a small angle θ, they combine to produce depolarizing noise. Thus, a rotation by angle θ in a dephasing environment produces substantial depolarizing noise, while rotating by angle θ with separate dephasing noise before and after this rotation produces only a small amount of depolarization.
I don’t think this is something I can explain in the comments of this blog, as I don’t know any easy way to write equations in it, but we can certainly discuss this via other channels. Gil has asserted in these comments that he doesn’t believe that this is true, but my impression is that he hasn’t worked out the equations. If he does work out the equations and finds in error in my analysis, I would really like to hear about it.
Peter and Aram, my impression is that the discrepancy regarding Peter’s example is that you do not take my definition for the distance between two systems but some different notions. To clear the difference, it may be useful to look at an example which is indeed approximately unitary which is the original context for my SLE. (Indeed, I did not look carefully at the specific noise Peter described since what I said did not depend on the identity of
.)
One can write latex formulas here by puting a dollar sign followed by the word “latex” before the formula and another dollar sign after the formula. E.g.
but I can pose here whatever Peter will transfer me in any channel (and fix any attempt to pose formulas directly).
I can’t speak for Peter, but I imagine that he is using the same notion of distance as me, which is variational distance in the transcript of measurement outcomes. Or even before that, the notion that “the results look very different and this is easy to detect with measurement(s).”
If there are N time steps for N large, and in one evolution, the identity operation happens each time step, and in the other, there is a 1/sqrt(N) chance of a bit flip in each time step, then the two evolutions will be close by the “average distance per time step” measure, but far in the more natural measures I describe above. Note that another flaw in the “average distance per time step” measure is that it is not invariant under rescaling time.
But the distance measure is a bit of a red herring. Peter and I have described consequences of SLE that just look like wacky unrealistic physics, and that are contradicted by the most basic experiments in any quantum system that we can manipulate coherently: nuclear spins, photon polarization, electron spins, atomic orbitals, you name it.
You mentioned that there was an example where SLE seems natural. What is it?
Indeed, my example was constructed so as to have a large variational distance in the outcomes of measurements at the end of the evolution.
If the evolution of two systems is “close” in some sense, but evolution 1 gives results which correspond to experiments, and evolution 2 gives results which have are at variance with experiments, I don’t see what good knowing that these evolutions are “close” does for you.
Peter wrote: “My belief is that smoothed Lindblad evolution cannot work unless the smoothing mechanism somehow depends on some property of the system which tells whether a real quantum computation is or is not taking place.”
Let me say briefly that I overall agree with this statement!
While you may agree with this statement in principle, your comments certainly seem to indicate you disagree with it in practice .
It’s funny that you and Klas regard my statements as saying something deep/excellent. Rather I am trying to say that the consensus view is that “there is some known physics that generates dynamics as a function of time,” then I describe that in terms of the most general/trivial/uncontroversial theories.
I would like to know how SLE compares with this consensus view. Does it generate predictions that deviate from known physics? Every time I try to analyze it for the simplest examples it gives predictions that seem to be nonsense. Exhibit A: my example. Exhibit B: Peter’s example. (You ask for a counterexample. Here are two. For a third, take any example where QM+noise yields any concrete prediction.) Where is the example where it seems to make sense?
“It’s funny that you and Klas regard my statements as saying something deep/excellent.”
Your question was excellent, Aram, since it demonstrated a deep misunderstanding that needs to be clarified. Let me try again
Aram: “But also I don’t understand the status of SLE. The consensus picture of quantum noise is that there is a Hamiltonian with terms for the system, the environment, and then terms coupling them. Tracing out the environment gives us some effective noisy evolution on the system. Assuming the environment is rapidly mixing yields the Lindblad formalism.
Is the content of the SLE conjecture that some part of that picture is wrong?”
No! Of course, not. As is very clear from the slides of my talk (and the formulas), including the few slides outlined in the post itself, the smoothed Lindblad evolutions form a special case of general Lindblad evolutions. (See also the reference in the presentation to the question of Lucas Svec.)
So how can you ask this question, Aram, when the answer is so obvious from the mathematics?
Gil,
I don’t think that Aram is disagreeing about smoothed Lindblad evolution being a special case of general Lindblad evolution. He’s talking about how you came up with the equations for smoothed Lindblad evolution.
In general, physicists don’t pick the Lindblad equation for a system out of thin air. They start with a Hamiltonian with terms for both the system interacting with itself and the system interacting with the environment. They then make the assumption that the environment is rapidly mixing (or at least, that the behavior of the system can be well approximated by ignoring the terms giving the environment’s interaction with itself, and replacing them by the assumption that the environment is rapidly mixing). They then trace out the environment.
Either that, or they do some experiments and figure out how to best fit the behavior of the system by a Lindblad equation.
I guess I asked the question because I am trying to use the idea of SLE to obtain predictions about what a system does. It seems to me that there are (at least) two possible ways to think about it:
1. SLE is a recipe for producing smoothed Lindblad evolutions. Start with some physically plausible Lindblad evolutions (like single-qubit decoherence) and then smooth according to some kernel.
2. SLE is an emergent property of (some) highly interacting Hamiltonians, just as Lindbladians are an emergent property of Hamiltonians in which the environment satisfies a Markovian condition. Thus to obtain the time evolution we need to start with some Hamiltonian (for which the conditions are unknown), and then come up with some kind of derivation that will show that SLE emerges as an effective theory.
3. something else entirely??
Peter and I have been responding to approach #1, arguing that it yields predictions dramatically different from what we observe in simple experiments.
But perhaps you had been thinking in terms of approach #2 all along? In this case, our criticism would still, I think, apply, but you might be able to argue that SLE is only an emergent property of Hamiltonians that have property X, and our examples don’t have property X. To which I would argue…, well, let me first pause to see what you think.
Aram’s question was indeed very good precisely because mathematically the answer is obvious. The SLE form a special case of general Lindblad evolutions so, of course, they do fit into the consensus picture of quantum noise: that there is a Hamiltonian with terms for the system, the environment, and then terms coupling them. The tension is not with the mathematics but with the interpretation and especially what the word “environment” refers to. (This was item #14 in the list of outlined issues of our debate.) In any case, the SLEs, and related classes of quantum systems that I consider, are all within the “consensus picture” as Aram defined it.
Hi Gil,
You say “they do fit into the consensus picture of quantum noise: that there is a Hamiltonian with terms for the system, the environment, and then terms coupling them.”
If this is so, then for some SLE describing a simple system, you should be able to explicitly give me the Hamiltonian with the terms for the system, with the environment, and for the system-environment coupling. You should be able to trace out the environment, after assuming that it mixes rapidly, and explicitly show how this gives me the Lindblad equation.
Physicists can do this for many simple systems, and get Lindblad equations which match reasonably well with experiment. From your discussions, you cannot do this.
Dear Peter, one way to think about my time-smoothing operation is as as a filter. My conjecture is that if you have a quantum system and if when you apply this filter the resulting tilde E_t has nothing to do with your original E_t, then you should regard your quantum system as unrealistic. So perhaps it is best to start with an explicitly given Hamiltonian with the terms for the system, with the environment, and for the system-environment coupling, (like the one proposed in the recent paper by Preskill regarding quantum fault tolerance,) and then once this explicit description is already given my condition will exclude as unrealistic a large number of such quantum systems based on overly exotic “term for the system”.
Two little remarks: First, there is no need to consider only Lindblad evolutions to start with. The conjecture that the system is well approximated (in my sense) by the smoothed version applies for more general systems. Second, indeed my condition is implicit.
This SLE-as-filter idea makes sense. In that case, should we think of it as similar to the “QC is impossible” conjecture? i.e. the conjecture is that many-body physics will, for perhaps many different reasons, always result in an evolution that can be described (1) by SLE, and/or (2) by something without as much entanglement as we would need for Shor’s algorithm.
Note that there is one sense in which all time evolutions can be described by SLE. Simply put all the time evolution into the “noise” terms E_s, and say that the “intended” time evolution corresponds to the Hamiltonian H=0. So I really think you have to address this concern about SLE requiring knowledge of our intentions in order to be well-defined.
However, using the naive definition of intended vs. unintended, I believe that my example (of a very noisy bit with a controllable coupling to a less noisy bit) shows a situation in which SLE is less realistic than the conventional picture, and indeed contradicts experiments. I think that Peter’s does too.
Aram: “Simply put all the time evolution into the “noise” terms E_s, and say that the “intended” time evolution corresponds to the Hamiltonian H=0.”
Aram, to avoid this and similar issues, in all my conjectures I consider the E_s as a POVM-measurement, and, in addition, I mainly consider approximately-unitary evolutions.
“Aram, to avoid this issue, in all my conjectures I consider the E_s as POVM-measurement, and in addition I mainly consider approximately-unitary evolutions.”
I don’t understand either of these points. It’s worth mentioning here that both the Kraus operator formalism (which is the generalization of POVM measurement that also models the output quantum state instead of assuming that it is discarded) and the unitary formalism are fully general and can describe all quantum evolutions. For example, {E_1, …, E_k} are a collection of valid Kraus operators if E_1^dag E_1 + … + E_k^dag E_k = I. But we can always take E_1 to be unitary and E_2 = … = E_k = 0, and thereby perform unitary evolution within this formalism. More complicated examples can easily make an effective unitary evolution that passes whatever simple criteria you want for being “noisy”, e.g. a unitary gate on the qubit you care about, together with some depolarizing noise on the qubit you don’t care about. So you cannot look at a process and say it is unitary or that it is noisy. Of course, you can say it involves interaction with an environment, but this depends on your definition of environment. Many things that we call “unitary” could also be called noisy; e.g. if our qubits are nuclear spins and we use RF pulses to control them, then the coil delivering the pulse could contain degrees of freedom that are considered to be “environment”.
Anyway, this might not address what you are actually talking about. My concern is that literally the definition of SLE contains a reference to our intentions. Maybe you could address it by writing a definition of SLE that does not mention our intentions? And in the process you might rule out my argument that all evolutions are trivially in the SLE class.
Let us fix a Hilbert space and a time window. On this Hilbert space let’s consider a unitary evolution which you can think about as the intended evolution. The SLE conjecture will say that the evolution will be subject to noise which is well approximated by a smoothed-in-time POVM measurement where the rate is lower bounded by a certain intrinsic parameter of the unitary evolution. (More specifically the rate in a time interval is lower bound by a non-commutativity measure of the evolution in this interval.) On top of this you can have additional standard noise. (Look at the last post of our debate.)
The interesting consequence from this conjecture or line-of thought is that smoothed-in-time noisy quantum processes, and in particular, smoothed Lindblad evolutions, are relevant for modeling realistic noisy quantum systems. Let me mention that the most interesting aspect of my work is not to refute quantum computing, via some no-go theorem of some sort, but rather to base interesting models of noisy quantum systems on the idea that quantum fault tolerance fails.
What you write leaves open the possibility that my intended unitary evolution is “nothing happens” but the noise process is “whatever quantum dynamics I secretly intended in the first place.” In this case, the process meets your definition of SLE without introducing any new (e.g. multiqubit) noise processes.
Aram, I think that I lost you. First, are you saying that every unitary evolution can be regarded as a small perturbation described by POVM-measurement of the identity evolution? And if the answer is yes, what precisely do you learn from this?
My point is that the POVM formalism and the unitary formalism are each, in a sense, universal. It’s like describing classical computation using CAs or Turing machines; each can simulate the other. Or like thinking of matrices as linear operators, or as rectangles full of numbers. They are just two ways of describing the same thing, and there is no assumption that anything is a small perturbation.
Thus, there is no canonical way to divide the evolution of the system into a “unitary part” and a “POVM part.” Yet the definition of SLE treats these parts differently.
I made this objection before, but it becomes more important when we try to do any kind of concrete calculation with, or make any kind of concrete statement about, SLE.
Hi Aram,
I realize that i have actually not stated what I believe myself on the issue of QC and fault tolerance, only what I think Gil have been saying.
I believe that in time universal quantum computers will be built. The engineering challenge is a non-trivial one, but I don’t see any fundamental obstacles against it.
That the machinery will affect the form of the noise, which I believe is Gil’s central thesis, looks obvious, and true for classical computers as well, but I don’t see any physical reason for why this feedback should as strong, destructive, and selective, as these conjectures imply.
At the same time I think the long Aram-Kalai debate has been useful, and interesting, since it has put a finger on some of the assumptions underlying error correction and the noise models.
Klas, it is worth mentioning that a standard assumption of FTQC is that the machinery affects the form of the noise, although of course it is always possible that the assumptions about this are not sufficiently pessimistic. But it’s not like this point was never considered before. It is in fact pretty central to many of the constructions.
Klas have made an excellent job in describing one crucial element of my point of view, and this is especially impressive given that he does not agree with my overall assessment. Aram is correct in saying that also in some standard models the machinery affects the form of the noise. The main problem (or the “trivial flaw” as I refer to it) is not that these models disregard the machinery or that they are too optimistic, but rather that these models are heavily based on the machinery being a general-purpose quantum computer. If you take this for granted, than you abstract away too much of the physics and then the failure or success of quantum fault-tolerance is essentially narrowed down to a single parameter.
I don’t understand your argument. If we try to apply the same reasoning to classical machines, doesn’t it work for them, too. If we have a noisy, special-purpose classical computer, we can’t use the fault-tolerance subroutine on it, and so when it gets large enough, it won’t work. Why is this an argument against general-purpose classical computers?
Or, maybe more to the point, what makes general-purpose quantum computers impossible but general-purpose classical computers possible?
“I don’t understand your argument.”
Peter, as said in the lecture my purpose is to describe a viable alternative for the possibility of quantum computers. To make it into an argument much more theoretical and empirical work is needed. (For some special cases, like topological quantum computing, I do offer an actual argument. ) Indeed, Klas understands but don’t “buy” this fragment of my proposed alternative picture.
“If we try to apply the same reasoning to classical machines, doesn’t it work for them, too.”
In the classical world sometimes this reasoning applies and sometimes it does not. If your computer (or brain) is used for composing a document and you suddenly decide to use it for computing the 10^8 zero of Riemann’s zeta function then this can be done by the same device. But If you ride your bicycle around the block and suddenly decide to take them for a manned mission to Mars, then you better replace your device. I agree that a quantum computer sounds analogous to a digital computer and not to a bicycle (After all, it is called “quantum c o m p u t e r.”) But we have to examine both possibilities.
“Or, maybe more to the point, what makes general-purpose quantum computers impossible but general-purpose classical computers possible?”
This was a central part of my debate with Aram. (See this post and this post.) My conjectures largely dodge this point, but I certainly discuss it in my papers and we did gain some interesting insights about it. Understanding the major difference between quantum computation (and fault tolerance) and classical computation (and fault-tolerance) is a major challenge to believers and doubters alike.
Aram, this is indeed a line of thought you expressed also in our debate. It is related to the thought that there is no objective meaning to “noise”. This is certainly an interesting foundational issue but I don’t see its particular relevance here. What is your conclusion, Aram, from the mathematical equivalence between the POVM formalism and the unitary formalism? What does it say, in your opinion, about open quantum systems? Or about quantum fault-tolerance?
When we fix a Hilbert space then there is a distinction between pure states and mixed states and between a unitary evolution and a noisy quantum evolution. We can talk about perturbations to unitary evolutions, and we can talk about noisy evolutions that represent approximately pure state for every time. (I referred to such evolutions as “approximately pure.”) Indeed let us fix both a Hilbert space and a time interval for the rest of the comment.
“Thus, there is no canonical way to divide the evolution of the system into a “unitary part” and a “POVM part.” Yet the definition of SLE treats these parts differently.”
1) When you restrict the unitary evolution of our world to a small Hilbert space then the restricted evolution is not unitary, This applies, in particular, to attempts to control a quantum system or to describe a quantum system on a small Hilbert space.
2) A reasonable description of such a system is in terms of a unitary part and an error described by POVM-measurement. (It is neither canonical nor the most general type of noisy quantum evolution.)
3) Smoothing-in-time can be regarded as a filter on the space of such noisy quantum evolutions.
4) If you give me a noisy quantum evolution described in terms of a unitary part and the POVM noise then I have a mathematical criterion to test if your evolution is realistic. In order to be realistic the filtered version of the evolution should be close (in a sense that I described) to the original evolution.
5) In view of this criterion I propose to study smoothed Lindblad evolutions as an interesting class of realistic noisy quantum evolutions.
The mathematical equivalence between the unitary and Kraus-operator (aka POVM) formalisms to me means that we cannot meaningfully base other definitions on distinctions between them.
Note that fixing the Hilbert space and the time interval are examples of looking at our intentions, unless your claim is that this holds for all Hilbert spaces and all time intervals, which I guess it is.
Let’s say that we do this, though. Fix a Hilbert space of our n qubits and call everything else the environment. Our control pulses are never perfectly unitary, as they always involve applying some kind of electromagnetic field controlled by noisy electronics. So we never apply a unitary. All we do is apply different kinds of noisy operations, some approximately unitary, some far from unitary. The set of unitary operations is measure zero in the space of all operations, just like low-rank matrices have measure zero among all matrices. There is no way a theory that makes predictions about observable outcomes can be sensitive to this.
Let me go back to two central issues raised by Peter.
1) Can you have smoothing on all time scales, and is my theory viable without it?
This was Peter first concern both in my lecture and his early comments (e.g. here). I thought that this is intriguing idea but I don’t see why it is necessary since I was talking all along about approximations and it is possible for a quantum system to be well approximated (in my sense) by an SLE for every time interval. I tend to agree with Peter that if you fix the Hilbert space you cannot have smoothing on all scales. (Note that the Hilbert space is also a “window” of a sort, just like the time window, and different scales are also represented by different Hilbert spaces.) Having a model with many-scales forms of smoothing when you consider both different time scales and different Hilbert-subspaces may be possible and quite interesting!
2) Can you determine the “correct” smoothing-scale from the evolution itself?
Ahh, this was a revised question that Peter asked. And here, I briefly said that I overall agree. (Both Peter and Aram are quite tough, Peter disagrees with me agreeing with him, and Aram criticizes me for referring to one of his questions as excellent. 🙂 ) So let me explain the matter less briefly.
My conjectures amount to the assertion that quantum noise for (genuine) quantum computation must accumulate. If this is the case then (genuine) quantum computing can only occur at a single time-scale. So, if the evolution is well approximated by an SLE on every time-scale, it follows that aposteriori there is a single relevant time scale. For shorter time-intervals nothing is happening and for larger time scales the decoherence takes over the system. It is not necessary for presenting the SLE conjecture to identify the relevant time scale, but the SLE viewpoint certainly suggests that this is possible. Indeed, I attempt of doing this as well, and you will see on the same slide of the SLE conjecture another conjecture relating the rate of noise with non-commutativity measure of the evolution. (The slide is outlined here in the post.)
Two more little points. First, I’d love to see the details of Peter’s example. (Please send me the details.) Do you have a similar example for an evolution which is approximately unitary? Second, I state a conjecture in terms of a certain distance measure for what “well-approximated” is. (On average for the time-interval the distance between E_t and \tilde E_t is small.) Since the conjecture is proposing a mathematical distinction between “realistic” and “non-realistic evolutions, why do you think that I should use a different distance measure? (Remember, the physical process is described by the original system, the smoothing only gives a criterion to distinguish between realistic systems and unrealistic systems coming from “thin air,” it is not meant to replace the original systems for making physical predictions.)
Gil,
Regarding the connection with SLE and the actual underlying physics.
As I understand it you don’t want to change any of the basic physical laws, among other things you want to leave quantum mechanics as it is.
Now, given any quantum circuit, or similarly described quantum process, which I will call Q we can from a purely mathematical point of view chose to couple it to any noise process N and then use quantum mechanics to find the time evolution of the joint system (Q,N).
As I have understood you one of your main points is that you think that for an actual physical system which implements Q the noise process N will be heavily influenced by Q so we are no longer free to use an arbitrary noise process N. In particular you believe that the actual noise process N will always be one with the property that the joint system (Q,N) will develop in time, following the standard laws of physics, in a way which is close, in some distance, to an SLE.
Your conjectures then does not say which specific SLE the system will follow, you expect that to be derived by considering the full system of Q together with the full environment using standard laws of physics, but since you conjecture that the result will always be close to an SLE that gives you a criterion for telling when a given noise process N shouldn’t be a physically valid one for the quantum process Q.
So your conjectures are all about which noise processes you think will appear in a physical implementation of Q, not about the underlying physical laws, and when you talk about an evolution you refer to the joint system (Q,N).
This is more or less the same as Aram’s point (2) regarding SLE as a emergent property
Is that a correct description?
GK: The short answer is YES.
Hi Gil,
Maybe I should go over my example.
My example is a very simple system: a qubit with dephasing noise. There are many ways to think of dephasing noise. One way is to think of it as applying a
to the qubit at Poisson intervals. (This effectively reduces the magnitude of the off-diagonal terms in the density matrix, multiplying each of these terms by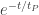 
.) Thus, the dephasing operator 
, where 
is a Dirac delta function on the points 
chosen by a Poisson process. Now, let us take 
given by the matrix ![[\cos \theta, - \sin \theta; \sin \theta, \cos \theta]](https://s0.wp.com/latex.php?latex=%5B%5Ccos+%5Ctheta%2C+-+%5Csin+%5Ctheta%3B+%5Csin+%5Ctheta%2C+%5Ccos+%5Ctheta%5D&bg=ffffff&fg=333333&s=0&c=20201002)
. If we rotate the qubit by a unitary gate 
halfway through the evolution, we should still get dephasing noise after we apply the matrix. We assume that the unitary gate is on a time scale much smaller than the time scale for the dephasing noise (i.e., the time scale for the Poisson process).
This system is simple enough that you should be able to do experiments and use tomography to get the exact density matrix at every stage of the process, so that you could do an experiment tracking the density matrix, and find that the experiment agrees with the dephasing noise at small time intervals throughout the process. I don’t know whether anybody has done this experiment, but I have no doubt that it would give the predictions of standard quantum mechanics.
Now, your SLE conjecture says that the noise before the application of the unitary matrix and the noise after it must come from some smoothed SLE. Since for smoothed SLEs, the noise at a time scale smaller than
tracks the unitary evolution, this says that whatever the noise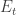 
was before the gate 
, the noise after the gate 
must be 
. This won’t agree with experiment.
If we took your conjecture to mean that we took whatever noise standard quantum mechanics gave us, and smoothed it, than the noise near the unitary gate will consist of discrete gates at Poisson intervals, with the operator equally likely to be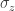
and 
. It is easy to check that 
. What this means is that the axis your qubit is aligned with does a random walk, changing by an angle 
each time. After a time roughly 
, where 
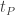is the time scale for the Poisson process, the axis of the qubit will likely have made somewhere near a complete rotation. This introduces depolarizing noise where there was none to begin with.
Even if you claim that there has to be some other noise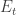
which gets smoothed, it can never be able to match dephasing noise both before and after the rotation, which is what has to be experimentally observed if we are to match the predictions of standard quantum mechanics.
Dear Peter, many thanks! I will certainly look carefully at this example, and your thoughts about it, Aram and Klas, are also most welcome.
Dear Peter, is this a reasonable summary of your claim and example?
SLE prediction according to Peter: When you genuinely implement a single qubit, which is subject to a dephasing noise in the time interval [-1,1] and a θ-rotation at time 0 you will discover, against the predictions of standard quantum mechanics, some amount of depolarizing noise. Peter claims that this prediction is clearly false.
Hi Gil,
That is a good summary.
SLE prediction according to Peter: When you genuinely implement a single qubit, which is subject to a dephasing noise in the time interval [-1,1] and a θ-rotation at time 0 you will discover, against the predictions of standard quantum mechanics, some amount of depolarizing noise. Peter claims that this prediction is clearly false.
This is a very good example, and thinking about it can be fruitful. There are two problems with this example. The first problem is that Peter’s prediction based on smoothed Lindblad evolutions goes well beyond my conjectures as they were (cautiously) stated by me. I will discuss it in the next remark. The second problem is that Peter’s SLE prediction is actually reasonable and, in fact, familiar. Let me discuss this point now.
Indeed there is another way to look at the SLE proposal which is the following. If you have a genuine noisy quantum computer (with a universal set of available gates) then the SLE evolutions give an appropriate way to model the noisy evolution of the computer. Note that with this interpretation the SLE replace the entire noise model and there is no specific treatment of gate-noise – the SLE should account for storage noise and gate noise together.
Suppose that we genuinely implement a single qubit and we can physically apply gates on this qubit. (This can be done at present in a variety of ways.) Suppose also that the dominant storage noise is that of a dephasing noise. Peter’s SLE prediction is that out of nowhere some depolarizing noise will be introduced around the time where the gate is applied. Is this realistic? (The answer is YES.)
Peter assumed that the unitary gate is on a time scale much smaller than the time scale for the dephasing noise, this assumption eliminated one possible reason for depolarizing noise, namely, that such a noise could have happened if the gate was “slow,” namely the θ-rotation could have happened gradually and interacted with the Poisson dephasing process. I don’t want to worry too much about slow gates since Peter’s scenario ignore a more basic reason for noise which is that the gate is inaccurate. If instead of θ-rotation we actually implement θ’-rotation where θ’ is a random variable concentrated around θ, then this inaccuracy introduces a depolarizing noise.
Peter’s SLE prediction holds because the gates which suppose to create a θ-rotation is imperfect and create a rotation with angle whose support is in a (small) neighborhood of θ. This can be expected in a genuine implementation of Peter’s scenario, and certainly in an implementation which is relevant to the issue of scalable systems.
In Peter’s example, Peter’s SLE prediction does not tell us anything very surprising. The standard models of noisy quantum computers also assume that noise on gates of an arbitrary nature cannot be avoided. Here the the SLE prediction is somewhat more detailed, it indeed proposes that for an appropriate modeling of a single-qubit gate we need to assume a certain amount of depolarizing noise.
Few remarks:
1) Peter wrote: “I don’t know whether anybody has done this experiment, but I have no doubt that it would give the predictions of standard quantum mechanics.”
Peter, this example demonstrates well that we are not debating the predictions of quantum mechanics. We are debating different ways for modeling realistic noisy quantum systems, including a realistic implementation of the experiment you proposed.
2) In this case Peter’s SLE prediction amounts to inaccuracy of gates, and assuming just arbitrary noise on gates does not exclude quantum fault-tolerance. The SLE predictions go further than that. (In fact, I also start them further than that.)
3) Since we are talking about a single gate on a single qubit, there are various ways of “shortcuts” and “cheating.” We can certainly simulate Peter’s scenario precisely as he described it on a digital computer. (Indeed this accounts for the cautious formulations of my conjectures.) These shortcuts are not relevant to the issue of modeling scalable noisy quantum processes.
Hi Gil,
The depolarizing noise caused by the inaccuracy of the gate can be quantified, as can the depolarizing noise caused by the SLE model of noise. For reasonable values of inaccuracy of the gate, they are nowhere near each other.
What you describe is called a “control error.” One tries to perform a rotation by theta and messes up a little bit.
Control errors do not look like SLE. The problem is that if the pulse lasts a microsecond, then control errors last for roughly that microsecond. But in Peter’s example, if your smoothing takes places over the span of a second, then we will observe depolarizing noise for that entire second. Control errors cannot do that, unless they are really extreme; i.e. we try to send in a microsecond-long pulse, and accidentally the button gets stuck and the pulse lasts for a second. But of course this does not resemble real life either.
I am using here the common-sense notion of “close”. However, I now think that SLE will look different from unsmoothed noise, even according to your definition. Let’s use the same parameters as above, plus say that the noise rate is on the scale of milliseconds, i.e. we experience dephasing every millisecond. Then every millisecond the random process will pick a random time T from 0 to 1 second and conjugate the standard noise (in this case dephasing) by the unitary evolution that has taken place over the past T seconds. Thus, for the 0.5 seconds after the applied pulse, there will be probability >= 1/2 of the smoothed noise being rotated by this pulse. Thus the difference will be substantial.
One more thing. When you write :
“You can have evolutions that are well-approximated by SLE in every time scale. (This applies, for example, to bounded depth quantum computing.)”
this is conjecture, right?
Or do you have a proof of this? It seems incorrect to me, in part based on Peter’s example.
Let me move to the second problem with Peter’s example starting with a quick summary.
A quick review of SLE idea.
1) My basic claim: SLEs give a realistic picture of noisy quantum evolutions.
Five remarks:
a) On top of this bad (or detrimental) noise introduced by smoothing, we may have some additional standard noise.
b) The Lindblad property is not crucial.
c) A separate conjecture discusses a lower bound on the amount of detrimental noise in a time interval.
d) I mainly consider approximately unitary evolutions where the noise is given by a POVM measurement and the state is close to pure for the time of the evolution.
e) SLE replaces the entire noise model of a quantum computer, both the storage errors and the noise on gates. Moreover it is not based on any qubit/gate description of the evolution and not even on a tensor power structure on the Hilbert space.
A quick review on the disagreements with Peter.
Peter: A) SLE cannot be taken seriously unless you exhibit time smoothing in every time-scale.
My response: I respectfully disagree: You can have evolutions that are well-approximated by SLE in every time scale. (This applies, for example, to bounded depth quantum computing.)
“Well approximated” is taken in the sense that on average over the time interval E_t and \tilde E_t are close.
(Peter and Aram disagree with this notion of distance. Since I use my notion of distance as a mathematical tool I am not sure what is the basis for Aram’s and Peter’s critique about it to start with. In addition, I am not sure if the critique applies in the regime of interest to me, namely when the state is approximately pure for all times.)
Peter B) Either you smooth on every time scale, or you “read” the relevant time interval for the smoothing from the evolution.
My response: I don’t agree that this is needed for the definition, but I do agree that it may well be possible to “read” the relevant time interval for the smoothing from the evolution.
(Peter disagreed with me agreeing with him , but based on my detailed explanation I hope he now agrees.)
Why Peter’s example is not relevant to the SLE conjectures as I posed them above.
What I argued in this thread is that SLE (or smoothing-in-time even for non-Lindblad evolutions) can be used as a mathematical tool to disqualify a large amount of noisy quantum system as unrealistic or, more precisely, irrelevant for modeling realistic noisy quantum systems. In my description, irrelevant processes are those where for some time interval the smoothed version is not a good approximation of the original system in a certain mathematical sense: The average distance between \tilde E_t and E_t is small. This criterion leaves alive Peter’s example without any difficulty. \tilde E_t and E_t will differs by much only in a small neighborhood of 0, the time where the gate is applied. As I mentioned my criterion leaves alive bounded depth quantum processes where the actual depth depends on the smoothing parameters.
Gil, when you write this:
” \tilde E_t and E_t will differs by much only in a small neighborhood of 0, the time where the gate is applied. ”
it seems at odds with everything I understand about SLE. Isn’t the point that you smooth over timescales much longer than the time necessarily to apply the gate?
Noise that is modified only while a gate is being applied is pretty uncontroversial, and not a problem for FTQC. In fact, something very much like SLE would be caused by simple timing errors, in which we apply the correct gate, but at a time randomly shifted from the desired time. In this case, there is a very definite timescale for the smoothing; it is the standard deviation of the timing error.
I still cannot (and I suspect Peter cannot) understand what it can mean for SLE to be valid and nontrivial in all timescales simultaneously. We are both trying.
I think Gil’s idea (correct me if I’m wrong, Gil), is that the computation goes from −1 to 1, and the smoothing is proportional to this time, with constant of proportionality ϵ, so there is only smoothing in the interval [−ϵ,ϵ]. This is still a large distance on either side of the gate, which happens at time 0. What I don’t understand is how the universe knows that we started watching this system at time −1, and we’re going to stop watching at time 1, so that it knows that the smoothing has to be on the time scale of ϵ.
In that case, your example could be modified to have a gate performed every epsilon/2 time steps (assuming that “1” = total time >> eps = smoothing time >> decoherence time scale >> gate speed).
Hi Gil,
I think I understand your intuition. It goes something like the following:
Physics experiments are analog, and quantum computation is digital. A small average distance between \tilde E_t and E_t will not change the results of an analog physics experiment much, but it will completely derail quantum computation.
I don’t believe you are correct about this not changing the results of an analog physics experiment much, and I think if you sat down and actually worked out the equations and the noise in my example, you would realize this.
Finally, I still don’t understand how the time scales work in your SLE conjecture. If you assume that the Lindblad evolution has been smoothing itself since the beginning of the universe, then I don’t see how you get any behavior that corresponds to standard physics. And if you assume that the Lindblad evolution is smoothed on a scale of ϵt, where t is the time scale for the quantum computation, you have to assume that the universe knows when you start and end your quantum computation. Neither of these assumptions seem to be tenable.
Three clarifying points, perhaps we can specifically discuss them.
First Point: The nature of my conjectures
I proposed a (mathematical) reality-test for a quantum system. Now, when you, a quantum information scientist, propose a quantum system, then, if your system passes my reality test you can stay with your system and use it for any physical predictions. If your system fails the reality test, then the conclusion is that this system is not realistic and cannot be realized at all.
Second point: The measure of distance
“A small average distance between \tilde E_t and E_t will not change the results of an analog physics experiment much, but it will completely derail quantum computation.”
No, this is not part of anything I said. What I said is that the average distance between \tilde E_t and E_t over a time interval is the mathematical measure I chose to define when a quantum system is close to an SLE over this time period.
Third point: What nature knows and what nature does.
” What I don’t understand is how the universe knows that we started watching this system at time −1, and we’re going to stop watching at time 1, so that it knows that the smoothing has to be on the time scale of ϵ.” “If you assume that the Lindblad evolution has been smoothing itself since the beginning of the universe, then I don’t see how you get any behavior that corresponds to standard physics. And if you assume that the Lindblad evolution is smoothed on a scale of ϵt, where t is the time scale for the quantum computation, you have to assume that the universe knows when you start and end your quantum computation.”
There is no smoothing that actually takes place, not from the beginning of the universe and not at any shorter time. Smoothing is a mathematical tool to express the systematic relations between a quantum system and the device (natural or human-made) needed to implement this system, and to describe the regime where these systematic relations are self-defeating.
“a mathematical tool to express the systematic relations between a quantum system and the device (natural or human-made) needed to implement this system, and to describe the regime where these systematic relations are self-defeating.”
This sort of makes sense, in the abstract, but when you try to compare it with any actual system, things go awry. Here is another example. I have a laser pointer. When I push a button, a laser comes out. When I let go of the button, then almost immediately the laser stops. The timescale of the smoothing is related to the internal circuitry of the laser pointer, but it’s generally pretty fast, and certainly there is _a_ timescale; it would be nonsense to say that this smoothing happens on ALL timescales. Where, then, is the systematic relation between system and device that resembles your description of SLE?
A more general point: I guess you want SLE to be emergent. But emergent from *what*? This would seem to imply that there is a universal theory of control/fabrication errors affecting everything we ever do.
Hi Gil,
I guess I was wrong when I tried to figure out your intuition.
But back to your conjecture. You now seem to be claiming that you want a reality test that any quantum evolution must be close to a smoothed Lindblad evolution. By your definition, isn’t any smoothing on an ϵt time scale for a process of length t small? This would mean that any evolution on [0,t] is close to a smoothed Lindblad evolution (you just smooth it with timescale ϵt). This would mean that you conjecture is completely trivial, and does not restrict quantum evolutions at all.
Could you clarify your conjecture so that I can actually understand what it says?
Back to the timescale.
I still think the time scale is a big problem. Why is the following reasoning incorrect?
You say that on a time scale from 0 to t, the evolution must be close to some evolution that is smoothed on a time scale of ϵt. Now, scaling this, you must similarly claim that the evolution from 0 to t/ϵ is close to some evolution that is smoothed on a time scale of t. But isn’t this equivalent to saying that the evolution on a random length-t time interval between 0 and t/ϵ is smoothed on a time scale of t? So most evolutions are smoothed on a time scale of t.
But now, if you just repeat 1/ϵ times the same experiment of length t, you realize that with reasonable probability the evolution must be smoothed on a time scale of length t. Is this a consequence of your conjecture, or is my reasoning incorrect somewhere?
Hi Gil,
Ignore the first of my two previous comments. My reasoning is wrong. For the second comment, I still think it’s correct.
Dear Peter and Aram, I hope things are now back to normal in your part of the world. Many thanks for the very good comments and issues that you have raised. I regard Peter last comment about time-scale especially excellent and right on the mark. I will try to relate to this point, rethink the general issue of time-scales, and relate also to some other points soon. It’s also ok to discuss Aram’s Laser pointer, but if we find out that it is not realistic, I am afraid, Aram, that you will not be able to use it no more. –Gil
Peter raised an ingenious argument regarding my SLE conjecture: Suppose that for a certain noisy (approximate) implementation of a unitary evolution and a certain level of approximation, δ is the maximum smoothing window that allows an SLE approximation of the required level. Say δ=0.5.
Now, suppose that we replicate, just implement this noisy unitary evolution a hundred times in a row. If the new evolution can be as well approximated by an SLE with a smoothing window ε this accounts for an approximation with smoothing window of min (100ε,1) on the intervals implementing the original evolution (or most of them), So δ must be larger than min (100ε,1) and since 100 can be taken as an arbitrary integer, this gives you ε=0 contrary to my conjecture.
This argument is correct!
It is based on the assumption that when we have a computation process we can repeat it several times and this will only takes longer. There is nothing that seems more obvious then that – it is true on our laptop, and it is true for the abacus.
However, this replication assumption is incorrect.
We cannot take it for granted for quantum computers, (unless, of course, we take for granted quantum fault-tolerance). It is possible that in order to realize (approximately) the original unitary process we need to build some complicated machine, and in order to realize the original unitary process three times in a row, we need a much more complicated machine, and that the evolution of repeating the unitary process 100 times without decoherence takes over is simply out of reach.
When you say the replication assumption is incorrect, I suppose you mean that this is your conjecture?
The problem with your argument is that it’s simply not true that doing more pulses requires building a different machine. Think about the laser pointer. It is one device, and I can push the button as many times, or as few times, as I please. Maybe I, the operator, need to be more complex to push the button many times, but if the laser pointer is causing an atomic state to make transitions, then surely you don’t want to conjecture that the complexity of my decision-making process is causing decoherence on the atom. Similarly with NMR (or countless other examples): we build one big NMR machine and then it is controllable by a classical computer.
The model of quantum gates with wires is mostly one we use on paper; it doesn’t really reflect how actual machines are built. Is that where your intuition is coming from here?
Aram, making the assumption that every unitary quantum evolution that can be created (approx.) can also be ran consecutively as many times as we want, is incorrect. This is a consequence of quantum fault-tolerance, but quantum fault-tolerance is required to achieve it, and if we want to examine if quantum fault-tolerance is possible we cannot take it for granted.
Of course, we do have noiseless classic computation, and classical computation can be repeated so that the only cost is longer time. (We also have your laser pointer.) We do need an explanation for which quantum evolutions the SLE noise can be zero, and, more generally, given a unitary (or perhaps more general) evolution what is the lower bound on the SLE-noise. One of my conjectures attempts to address this issue. Certainly more can and should be done here.
In any case, the assumption that for every unitary quantum evolution that can be approximated empirically, you can also achieve this for an unlimited repetative evolution is incorrect in the context of our discussion. I think that it is incorrect even when it comes to evolutions of a single qubit.
I didn’t say *every* unitary could be, just a parameterized family of unitaries. But I don’t see what fault tolerance has to do with anything here. For many examples, we are talking about one qubit (e.g. Peter’s example) or two qubits (e.g. mine), where nothing is fault tolerant.
There are many quantum systems where I apply some controlled field and then the system reacts. You keep saying that something goes wrong if I do this repeatedly, but I don’t see any support for this claim, apart from invoking the “trivial objection” which doesn’t count if what is causing the repeated action (i.e. the human experimenter) can be reasonably assumed not to be in a complicated entangled state with the target system. Note that I am *not* arguing that the overall evolution is unitary. Certainly there are control errors and noise. However, noise doesn’t mean that everything breaks down after some amount of time, and we just throw our hands up in the air. SLE, if valid, should give valid predictions even in regimes where there is too much noise to do quantum computing.
FTQC is very complicated (as is FTCC for that matter), and neither can be defined in a non-asymptotic sense. So before talking about SLE’s effects on FTQC, we should try to totally understand if it gives mathematically well-defined and physically plausible predictions for one and two qubits.
Aram, suppose we consider an implementation of quantum computing on a single qubit, and we wish to pass the qubit by a sequence of length fifty of X and Z rotations with a certain angles. This is something that can be implemented today with pretty good fidelity. This does not mean that you can implement a sequence which is a 100 times the original sequence. In fact, the noise in such systems accumulates and Peter’s assumption is incorrect even for this simple systems.
It is true that you can control your laser pointer and your car quite perfectly and that on some level some quantum process is taking place both in your laser pointer and in your car. But I don’t think that these examples are very relevant to Peter’s specific claim regarding time-scaling that we are discussing.
Why do you say that Peter’s assumption (and which assumption?) is wrong on such simple systems? If the assumption is that the system can be well described without SLE, than that seems fine to me.
If you apply a series of 100 pulses of different angles, I’m not claiming that you will have something with high fidelity to a pure state afterwards. In some cases you would, but in many cases, there will be too much noise for this. However, “very noisy” doesn’t mean that SLE automatically applies. Indeed, in both my and Peter’s examples, there is a lot of noise (enough to destroy a qubit many times over), but that noise doesn’t look like SLE.
Finally, I think a big problem with SLE is however you define it, it can’t help but give different predictions on single-qubit systems. But those systems are too simple to hide any radically new behavior.
Gil,
In order to repeat the computation in a quantum computer many times, we need to be able to reset some of the qubits to the initial state, say |000..0>. Without this ability, a thermodynamic argument of Aharonov et al shows that it’s impossible to do any computation of more than logarithmic depth.
However, it is possible to reset qubits, both in most physics experiments and in the Lindblad evolution model (although not in a strictly unitary model): simply apply amplitude damping noise to the qubits you want to reset. If you’re saying that repeating a quantum physics experiment many times requires more resources than simply time and an ability to reset the experiment to its initial state, you are going against both intuition and decades of experience of experimental physicists. If this is what your smoothed SLE noise model predicts, I think the evidence against it is overwhelming.
Dear Peter,
I have no problem with the assumption that we are able to reset some of the qubits to the initial state, say |000..0>.
“In order to repeat the computation in a quantum computer many times, we need to be able to reset some of the qubits to the initial state, say |000..0>.”
The way I see it, in order to repeat the computation many times we need to be able to apply quantum fault-tolerance which relies on 1) Certain assumptions on the noise model and rate of noise, AND 2) being able to reset some of the qubits to the initial state, say |000..0>.
My SLE model (and other conjectures) challenge the noise model and not the reset assumption. The result of Aharonov, Ben-Or Impagliazzo and Nisan, shows that even under the ordinary noise model, without the ability to reset we cannot do long (more than log-depth) quantum computing.
Your argument regarding scaling and SLE is based on the ability to repeat, which is based on the ability to have quantum fault-tolerance. I certainly agree that the SLE model is in conflict with quantum fault-tolerance, in fact, this is the whole idea.
“If you’re saying that repeating a quantum physics experiment many times requires more resources than simply time and an ability to reset the experiment to its initial state, you are going against both intuition and decades of experience of experimental physicists.”
The term “repeating a quantum physics experiment” is a little ambiguous. We are talking here about repeating many times in a row the same sequence of unitary steps without being killed by decoherence. I completely agree that saying that this is not possible goes against the intuition that quantum fault-tolerance is possible, and against the intuition coming from classical computing. I am not aware, however, that this assertion is in conflict with decades of experimental physics, but will certainly be happy to learn. I think that the picture I draw is actually consistent with the experience we have (so far) in experimental quantum computing. It is possible that this experience will change once a certain threshold is met but this depends on the crucial question of how quantum noise should be modeled.
Let me repeat that we have no disagreement about the possibility to reset, only about the models of noise. In any case, your point about the ability to run a sequence of unitary steps many times in a row is right where the crux of matters is.
In the scenarios Peter and I are talking about, the state may still be “killed by decoherence.” But this doesn’t mean that there is no information in it; simply that entanglement with a reference system wouldn’t survive. e.g. in Peter’s example, dephasing noise merely destroys the off-diagonal terms of the density matrix, and in my example, one bit lasts a long time and the other is quickly randomized. So SLE should give correct predictions even in this case as well. And saying “SLE predicts there is lots of noise, and the true evolution predicts lots of noise” is NOT enough. Peter and I claim SLE will lead to a *different* type of noise, and thus contradicts experiment.
But as I said, one and two qubit systems pretty much react the way theory predicts, with noise that is described fine w/o SLE. So anything like SLE had better give nearly identical answers (with “nearly identical” being in the metric of “experiments give nearly indistinguishable outcomes”) or else it will contradict experiment.
GK: Dear Aram, My comments in this sub-thread are not referring to the examples by Peter and by you, but rather to the specific point Peter had made about the time-scaling issue. I promise to think further and come back to these two examples.
Hi Gil,
My comment about resetting the system was partially based on your statement:
“Aram, suppose we consider an implementation of quantum computing on a single qubit, and we wish to pass the qubit by a sequence of length fifty of X and Z rotations with a certain angles. This is something that can be implemented today with pretty good fidelity. This does not mean that you can implement a sequence which is a 100 times the original sequence. In fact, the noise in such systems accumulates and Peter’s assumption is incorrect even for this simple systems.”
I would predict that the noise in such systems only accumulates if you don’t reset the system between repeating the sequence.
I don’t understand why a quantum computation that we can do fine if we do it once should suddenly go haywire when we try to repeat it (assuming that we properly reset the system between repetitions). After all, even if we don’t repeat it, the qubits that we are using must have had some history before the start of the experiment. Why shouldn’t this history interfere with the experiment in the same way that repeating it did?
Dear Aram and Peter,
Here are a few further thoughts on some points that we discussed. Let me start with another thought on the time-scaling issue.
1) Rethinking the smoothing’s time-scaling issue: I still think that there is no problem talking about evolutions which well-approximate SLE in every time scale (in my distance), but, I agree with Peter that the relevant smoothing-scale could be read from the evolution itself. Here is an idea on how this should be done: I think that in modeling smoothed-evolution we can take the scale for the smoothing to be the same as a normalized rate of noise. Namely, if the rate of noise at a certain time is such that an uninterrupted noise of this rate can lead to loosing coherence in time T then the smoothing window should be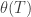
.
As I said, there is an additional conjecture that the rate of smoothed-noise at a time-interval is lower-bounded in terms of a certain non-commutativity measure. In particular, this conjecture describes cases where the SLE noise can be zero.
(It is also interesting to start with ordinary assumptions on the noise of quantum computers, then smooth the noise, and see if we can recover noiseless classical computing. In fact, this was the one-before-last open question in my debate with Aram.)
2) Scope: As mentioned before, I am mainly interested in the case of evolutions where the state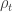
is approximately-pure along the time t of the evolution. (Perhaps the measure most suitable for “approximately pure” is that the entropy is bounded by a small constant times the maximum entropy. ) The SLE description should extend further but (like in other cases) it may require more thinking on how to do it right and how to interpret it right.
3) Bounded depth quantum computation: If the computation is of bounded depth D then for an appropriate smoothing window (roughly of the order of 1/D) the smoothed noise is close (in my sense) to the standard noise. Aram asked if I have a proof of this, and I indicated a proof before. It seems quite obvious from the definition of \tilde E_t.
4) Peter’s example: My main point was that applying one gate or a few gates in a row is well approximated by SLE for an appropriate smoothing window. (Well-approximated in my sense). If you repeat an interesting sequence of unitary steps many times then we come back to the repeating issue. (I made a secondary point that smoothing in the much more abstract setting of SLE may recover some realistic properties of gate-errors in the much more specific gate/qubit model, again in the near-pure regime.)
5) Aram’s example: I did not think much about it yet, and I am also confused by Aram referring to his example in terms of bits. Is this an essentially classical system?
6) Single-qubit systems and disagreement with some predictions:
Aram: “Finally, I think a big problem with SLE is however you define it, it can’t help but give different predictions on single-qubit systems. But those systems are too simple to hide any radically new behavior.”
I do not agree with this statement. It is a common belief that without quantum fault-tolerance (possibly on the microscopic level) you cannot reach noiseless viable qubits, or in other words, there is a limit to the number of operations you can achieve without using some mechanism of quantum fault-tolerance. When there is a bound D on the number of steps you can achieve, the SLE approximation is close to your original system for smoothing window of ε(1/D). Indeed in this case the smoothing window is proportional to the rate of noise itself, and this is in agreement with the first point above.
My conjecture is that realistic systems (perhaps, after ignoring some amount of standard noise) can be well-approximated in a certain mathematical sense by SLE. This gives a mathematical distinction between realistic and non-realistic evolutions and it does not mean that every physical prediction of a quantum system will apply to its smoothed version. As I said, I suggest to think about the smoothing as a filter. The conjecture is that the filtered system is close to the original system. It is not that every physical property of the original system is carried over to the filtered system.
7) Sigle-qubit computing with resets.
Peter: “I would predict that the noise in such systems only accumulates if you don’t reset the system between repeating the sequence.”
Yes, I completely agree with that. What I was saying was that if you run a unitary computation on a single qubit then in present (and foreseeable) technology the noise accumulates. The whole purpose of the smoothing is to express formally the term “the noise accumulates,” for nearly-unitary/nearly-pure evolutions.
When you run a non-unitary sequence of the form Reset, X-rotation, Z-rotation, Reset, X-rotation, Z-rotation, Reset X-rotation Z-rotation etc. then I agree that you can run it forever.
8) Disagreement about distance: I don’t agree with (and not fully understand) Peter and Aram’s objection to my measure for distance.
9) What is noise: I disagree with Aram’s general stance regarding noise. We discussed it several times in our debate. The question of the correct way to approximate unitary evolutions looks both real, crucial, and very relevant to many things.
10) Our multi-scale world. My conjecture asserts that (genuine) quantum computing occurs in a single time scale. This suggests that different scales in our multi-scaled world “communicate” via classical information, namely the effect of a finer scale on a coarser one can be described in terms of classical parameters.
11) Windows and intentions. Aram: “Note that fixing the Hilbert space and the time interval are examples of looking at our intentions, unless your claim is that this holds for all Hilbert spaces and all time intervals, which I guess it is.”
Yes, this is what my claim is.
Just a few comments.
1,3) Your argument about why SLE shouldn’t affect bounded-depth quantum computation is incompatible with the scaling problem. I’m not sure whether you are convinced yet that there’s a scaling problem, but if you do admit there is one, you should rethink point 3).
2,7) We don’t need SLE to explain why the noise accumulates for unitary evolution without false tolerance. Fault-tolerant quantum computation is not nearly unitary (not even, I believe, in the sense of 2)). It is only nearly unitary on the protected subspace that the evolution is taking place in.
If your SLE conjecture implies that there can be no such thing as a protected subspace, I don’t believe this agrees with experiment. There is a protected subspace in the fractional quantum Hall effect (which is why it can be used for quantum computing). I don’t know whether your SLE conjecture would destroy the fractional quantum Hall effect, but my guess is that it would. If not, there needs to be an explanation for why SLEs leave the protected subspace alone in the fractional quantum Hall effect and not in fault tolerant quantum computing.
8) Our objection to your distance is that in our intuition, evolutions that give measurably different outputs should not be close in distance. If you’re saying two evolutions separated by a small distance are essentially the same, then they really shouldn’t be distinguishable.
Hi Peter,
Metric, scaling
Let me start with point number 8. “If you’re saying two evolutions separated by a small distance are essentially the same, then they really shouldn’t be distinguishable.” Actually my measure is just between the non-unitary parts of the two evolutions E_t and \tilde E_t. Maybe the terms “well-approximated” is responsible for the intuition of Aram and you. Another way to say it, perhaps, would be that the smoothed noise keeps much information of the original noise. In any case, when I try to make a mathematical distinction between classes of Lindblad evolutions, I think I can choose the mathematical tool.
Regarding the scaling issue and bounded depth evolutions: It is strange that we disagree on a matter which is (almost) purely mathematics. Is your claim depending on rejecting my metric (point 8)? Anyway, since this is a mathematical issue we cannot agree to disagree and I am truly curious what is going on. The way I see it, bounded depth computation pass the SLE test (with my metric) with no difficulty…
Let me relate now to the new very good points:
“We don’t need SLE to explain why the noise accumulates for unitary evolution without false tolerance.”
The main point here is of using SLE to express the property that noise accumulates for unitary evolution without false tolerance. Overall, I agree with much of what you wrote.
There are two ways to look at my conjectures, one way (which I prefer) is to consider them simultaneously for every window of Hilbert-space and time interval. Looking at them this way then, of course, they violate quantum fault-tolerance since they don’t allow protected (noiseless) unitary evolutions on some protected Hilbert space.
The other way (also interesting) is to consider the conjectures as describing noise-models for noisy quantum computers. Here indeed you do need to extend the discussion to certain non-unitary evolutions. You need to allow introducing noiseless qubits with a |0> state: (We can actually have them from the beginning and since they are not manipulated, I allow E_t to be 0 for them.) But we also need to discard some qubits and then never apply them again. My impression is that the SLE framework can be applied here and then the challenge would be to deduce from such a noisy model of QC that FTQC cannot work.
Protected subspaces and fractional Hall effect
Let’s go back to the first point of view. You wrote: “I don’t know whether your SLE conjecture would destroy the fractional quantum Hall effect, but my guess is that it would.”
This is worth exploring because if your guess is correct then my conjectures are flatly dead!
You also wrote: “If your SLE conjecture implies that there can be no such thing as a protected subspace, I don’t believe this agrees with experiment.”
This is putting it too strongly. You can have protected subspaces but the behavior of noisy quantum evolutions on these protected subspaces cannot behave any better than the behavior of noisy quantum evolutions on “ordinary” Hilbert spaces. (E.g. you can have a stable ground state, and even stable excited states, but general enough superpositions are necessary noisy..)
I should say that my guess is that the fractional quantum Hall effect does not contradict my conjectures. What I need to understand better is how you think about it as a protected subspace, and when restricting to this subspace what are the evolutions and what is the nature of noise. In particular, how (realistic) quantum Hall effect non-pure states are described?
One reason for my guess is that my conjectures are easier to believe for quantum states created by a quantum process which does not involve quantum fault-tolerance.
Hi Gil,
Protected quantum subspaces should be degenerate or nearly so: all states have almost exactly the same energy (so there are no ground states, excited states, etc.)
But it’s certainly possible you could have protected subspaces that you are unable to do computation in.
1. Gil: “If the rate of noise at a certain time is such that an uninterrupted noise of this rate can lead to losing coherence in time T then the smoothing window should be Theta(T).”
This is not totally well-defined, because “losing coherence” means that data is lost, but different (qu)bits may lose coherence at different rates.
However, it is already enough to generate different behavior from standard noise models in Peter’s example.
Recovering classical computing is an interesting idea, but I believe that analyzing SLE in this case would lead to unrealistic high failure rates of classical computers. Since this is complicated, I propose instead starting by analyzing two bits carefully.
2. The evolution cannot depend on whether rho is pure or mixed; this is like knowing whether I prepared the state of the system with a firm intention to prepare a given state, or whether I first flipped a coin to help me decide how to prepare it. Also, we can always purify mixed states by adding a reference system. You want SLE to describe only nearly-pure evolutions, but if it does so, then it must also describe evolution of any mixed state.
3. Do you mean a window of length D? D has units of time, 1/D units of frequency, and the smoothing window has units of time. Is there some other timescale that, besides D, that you want to introduce? I am really confused here. It seems to me the only time you get that tilde{E}_t is trivially close to E_t is when the smoothing window is much less than the time required to implement a single gate. Where is the proof you mentioned?
5. My example is essentially classical, in that thinking about it classically will capture all the essential features. Of course, it could equally well be quantum. A high rate of dephasing simplifies things, but isn’t necessary. I definitely believe that if SLE is strong enough to derail quantum computing, then it must also do the same to classical computing, but I also think that those examples are too complicated to productively discuss.
6. When you say that without FTQC we can’t have viable qubits, this is only true with an extremely ambitious definition of “viable.” We can do a lot with single qubits, including performing millions or even billions of unitaries before they decohere. We can also dynamically reset them. Yes, there is always some noise, but we usually understand this noise and our models for the noise generally exhibit close matches between theory and experiment. SLE would cause different behavior (e.g. in Peter and my examples), and so doesn’t work.
7. I don’t think SLE is the correct formulation of “the noise accumulates” because it leads to entirely new forms of noise not predicted by current theory or seen in current experiments (e.g. our examples). Also, resetting gets rid of noise (while getting rid of data at the same time), so I wouldn’t even say that “the noise accumulates” is a good way to describe non-fault-tolerant single qubits. Perhaps “data is not preserved” would be better.
8. I don’t think our disagreements about distance matter that much. I think it’s fine that we use different distance measures. I think that Peter and I are using a distance measure which describes experimental distinguishability; i.e. two processes are far apart iff some experiment can distinguish them. Your measure is indeed different, but I think it doesn’t matter unless the statement of your conjecture depends somehow on this distance measure.
11. I suspect there is no mathematically consistent way to define evolution that is described by SLE for all Hilbert spaces and all time intervals, apart from trivial cases, such as having no noise and no interaction.
OK, let me explain why for a bounded depth D evolution, if the smoothing window is ε/D then the smoothed noise \tilde E_t is close to to the original noise E_t. Let us smooth with respect to the whole computational interval. Recall that \tilde E_t is the integral of K(t-s)E_s, and that K(t-s) is very small out of a window of length ε/D around zero. This implies that \tilde E_t and E_t are very close except for D intervals of length ε/D, so the expected distance of E_t and \tilde E_t behaves like ε. (Maybe I wrote D instead of 1/D at some point..)
If you apply the smoothing with respect to a smaller window then the situation is even better.
So far, this is pure math. If you consider larger windows we do need to make some assumptions on how the unitary evolution itself extends. If the unitary evolution outside the time interval is the identity then this was discussed in some early comments and the conjecture is fine. If the unitary outside the computational interval is repeating the computation many times then the smoothing conjecture is violated but I think that we simple cannot assume such an evolution.
If you want to reset and start again then this is not a unitary evolution, so the conjecture does not apply. Indeed, I think that some version for some larger Hilbert space should apply but then we need to carefully work out the situation.
On another matter: “We can do a lot with single qubits, including performing millions or even billions of unitaries before they decohere. We can also dynamically reset them.” A crucial aspect would be to understand how, without FTQC for general evolutions, the possible depth scale down with the number of qubits. But I admit that the ability to perform milions or billions of unitary steps on a single qubit is already in tension with what I say. Can you elaborate on that?
This is helpful, but let me rephrase to make sure I understand.
If the evolution has depth D and you smooth over a window of time eps/D, then there is still a timescale that is missing, which is how frequent the gates are. Are you saying that the total time for the computation is 1 (let’s say 1 second) and the gates happen every 1/D seconds? If so, then yes, I understand why smoothing with a window of size eps/D will not change things very much, with respect to your metric. Although after 1/eps gates, this will still produce an observably different outcome, and so will contradict existing experiment.
When you write “If you want to reset and start again then this is not a unitary evolution, so the conjecture does not apply.” this is serious, since nothing is _exactly_ unitary (unless we are talking about evolution of the entire universe), and usually deviations of unitarity are significant, including in all known FTQC proposals. Indeed this is the point of the 1996 Aharonov-Ben-Or-Impagliazzo-Nisan paper.
As for performing billions of unitary steps on a single qubit, I’m having a hard time finding references. The basic phenomenon of repeatedly applying sigma_x gates to a qubit is called “Rabi oscillations”; see here:
http://en.wikipedia.org/wiki/Rabi_cycle
The reason I’m having trouble finding examples of billions of Rabi oscillations is that usually people measure the lifetime when no pulses are applied. Googling came up with this example with 3500 consecutive pulses, but I will ask around for longer examples.
http://arxiv.org/abs/0801.4126
Hi Gil,
I now see how you’re getting around my argument about the time scale: You’re saying that if you want to stop and restart again, this is not unitary evolution, so SLE does not apply. However, fault-tolerant quantum computation continuously “stops and restarts” the computation again on the level of the errors, because it needs to continuously throw away noisy qubits and replace them by fresh ones. It is unitary only on the protected subspace. So actual fault-tolerant quantum computation is nowhere near unitary evolution.
I don’t at all understand how you would apply the SLE criterion to fault-tolerant quantum computation. My guess is that you are going to say that the SLE conjecture should apply only on the level of the protected subspace, and not on the level of the errors, but how do you plan to separate these “levels”? It seems to me that they’re irreversibly intertwined. I would like to see some actual mathematical definition for how to accomplish this separation.
Right,
If you add the restart to the evolution then I would not consider the evolution as unitary.
As I said in my previous many-item comment there are two ways to think about the conjectures (and I propose think about both of them).
The second way I described is actually to consider the non-unitary evolutions described by fault tolerance scheme. Namely to consider the conjectures as describing noise-models for noisy quantum computers. Here indeed you do need to extend the discussion to certain non-unitary evolutions. You need to allow introducing noiseless qubits with a |0> state: (We can actually have them from the beginning and since they are not manipulated, I allow E_t to be 0 for them.) But we also need to discard some qubits and then never apply them again. (So I dont think we need to actually “restart” qubits.) My impression is that the SLE framework can be applied to this class of non-unitary evolutions but it certainly need to be very carefully carried out.
The first way to think about the conjectures is to consider them simultaneously for every window of Hilbert-space and time interval. Looking at them this way then, of course, they violate quantum fault-tolerance since they don’t allow protected (noiseless) unitary evolutions on some protected Hilbert space. (The SLE conjecture does not depend at all on a qubit tensor structure.)
Of course it will be very nice to have a theorem saying that if you assume the conjecture as a model of noise for the quantum computer then you can deduce the conjecture for any sub-Helbert space. But I dont have such a theorem.
Since I see it more important to try to formally describe how realistic quantum evolution behaves (or how quantum evolutions without quantum fault-tolerance behave) than to prove a no-go theorem for FTQC under a certain model, I like better the more drastic way of thinking about the conjecture. (I regard quantum fault-tolerance as representing a major phase transition even if it is possible, so for me studying quantum systems on “our” side of this phase transition makes sense even if QC are ultimately possible.) But certainly relating these two approaches via a mathematical theorem would be a major step.
So in short, the SLE idea should work both on the levels of the errors for the “raw” qubits and on the level of protected subspaces, and the hope is that assuming the conjecture on the raw level (which requires extension to certain nonunitary cases) will allow proving them for the protected level.
But I realized yet another potential “loophole” regarding your restart idea, Peter, let me challenge you guys with it.
Suppose that we have a few unitary steps that we repeat. But now we consider the restart operation as part of the noise! this noise is not well approximated by its smoothed version (for the whole time-scale) at all. Is looking at this in this way violate my conjecture?
Here is the answer: My conjecture is that “realistic systems (perhaps, after ignoring some amount of standard noise) can be well-approximated, in a certain mathematical sense, by SLE.” The restarts steps, lookd at as noise, represent standard noise that we need to ignore.
Hi Gil,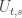
that we can use to evolve the decoherence $E$ from the qubits on which standard quantum mechanics predicts it is taking place to the protected subspace.
For quantum fault tolerance, the “raw” decoherence, i.e. that predicted from standard quantum mechanics, is incredibly small on the protected subspace (which I assume is why came up with the SLE conjecture). Any decoherence must be inherited through the SLE phenomenon. But the qubits to which the decoherence is actually happening are constantly being thrown away and replaced by new qubits. So as far as I can see, there’s no underlying unitary evolution
Gil,
Your proposal to ignore “restart” noise seems to me to incompatible with your SLE proposal. Let me explain why.
Suppose we have continuous, but small magnitude, amplitude damping noise on every qubit. If we let a qubit sit untouched, the amplitude damping noise eventually puts it in the state |0>, effectively resetting the qubit. I take it that your reasoning means that in this case, we should ignore the amplitude damping noise.
If we continuously apply a rotation to each qubit (so that the amplitude damping noise acts on the logical qubit from every direction), the amplitude damping noise turns into depolarizing noise. I assume that, in this case, you believe we should convolve the amplitude damping noise using the underlying unitary evolution as in your SLE conjecture.
But I believe there is no way to distinguish these two cases without analyzing the underlying quantum computer program, since you can reset logical qubits with amplitude damping noise even if you shuttle these logical qubits between different physical qubits and have them interact using quantum gates (e.g., using a CNOT gate between two qubits that are being reset with amplitude damping noise should not slow down the rate at which they are reset).
1) Moving from SLE as a noise model to SLE for “protected” subspaces.
Peter: “For quantum fault tolerance, the “raw” decoherence, i.e. that predicted from standard quantum mechanics, is incredibly small on the protected subspace (which I assume is why came up with the SLE conjecture). Any decoherence must be inherited through the SLE phenomenon.”
This is correct. The standard noise model allows to have (essentially) noiseless evolution on decoherence-free subspaces. Decoherence on these protected subspaces must be inherited through the SLE phenomenon.
“But the qubits to which the decoherence is actually happening are constantly being thrown away and replaced by new qubits. So as far as I can see, there’s no underlying unitary evolution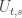
that we can use to evolve the decoherence $E$ from the qubits on which standard quantum mechanics predicts it is taking place to the protected subspace.”
As mentioned above, the framework of quantum fault-tolerance is only a small extension of the unitary case, and the SLE formula can be applied there. We need to add two ingredients. The first ingredient is the ability to introduce fresh qubits, and we can simply regard these qubits as being there from the beginning of the evolution, and set the noise E_t (before smoothing) acting on them as zero until the time they get into action. The second ingredient is the ability to ignore some noisy qubits at some times, and these qubits never participate in any interaction after that time.
It is an interesting mathematical conjecture that if you assume an SLE noise for the (entire) quantum noisy computer (where E_t can be a very standard noise), then the evolution on every “protected” subspace will be subject to substantial noise which is also an SLE noise.
I have one 2008 result with Greg Kuperberg related to this conjecture… but in the opposite direction! (Recently Greg told me that he intends to make it into a short joint paper.) The result implies that if K(x) is supported only on non-negative values of x, (so the noise does not depend on the “future” of the unitary evolution,) then fault-tolerant quantum computation is possible. Greg proposed a wonderful provisional title: “Preventing quantum computation requires time travel.” In any case, it will be interesting to prove that if K(x) is supported on the entire interval then the SLE-noise is inherited to subspaces and that FTQC is not possible.
(Of course, if you take the SLE conjecture to apply to all subspaces and not just on the level of the physical qubits then this automatically excludes FTQC.)
2) Combining smooth and non-smooth noise.
There is an important point that I have mentioned many times but that I should have emphasized earlier in this discussion. (In fact, neglecting it in some of my comments above caused some confusion also to me.). My conjecture does not assert that the entire noise is a smoothed-time noise (exactly or approximately), only that some component of the noise is a smoothed-time noise. So in addition to a smoothed-time noise there can well be some standard noise. To account for that, in the MIT presentation (and the debate with Aram) I allowed in the definition of SLE the kernel K(x) to have an atom at 0. In hindsight, this atom makes things more confusing, especially in the context of time-scaling that we discussed here. So I propose, from now on, to require that the kernel K(x) is smooth (say truncated Gaussian) without any atom at zero, and then the conjecture is that a realistic noise for a unitary evolution includes some SLE (or rather some “all-timescales-approximated-SLE) noise component.
When we consider smoothed noise in addition to other types of noise, the conjecture is less interesting for evolutions of one qubit (or even for evolutions of two interacting qubits). If you have a one-qubit quantum system based on a sequence of unitary evolutions for the time interval [-∞,∞] then as long as you have some small-rate depolarizing noise your system is subject to an SLE noise. So the conjecture “kicks-in” in an interesting way only for more qubits. (For every Hilbert space and every evolution a “global” depolarizing noise is an SLE noise, but, of course, we do not regard this type of noise realistic when there are more than a few qubits.)
3) When we have a natural tensor product structure, it is reasonable to consider noise which acts independently on the different components. For certain evolutions this type of noise is not smoothed-in time and I expect an additional smoothed-in-time noise with very different behavior, so the overall noise will have two distinguished components. This type of dichotomy may be relevant to quantum systems and states related to protected subspaces. What you may get is that you will indeed recover exciting protected subspaces, which may represent a new phase of matter, but, intrinsically, the nature of noisy quantum systems on these subspaces will be familiar, and will not exhibit the remarkable expected robustness.
If you protect fresh qubits from smoothed noise (and note that qubits don’t have to be literally new; they can be old qubits that were reset using amplitude damping processes) and smoothed noise doesn’t move through measurements (else it would infect our brains and classical computers) then FTQC is trivially possible via meaurement-based schemes in which each qubit is touched only a constant number of times between its initialization and final measurement.
Aram, I suppose that the noise before smoothing is 0 for fresh qubit before they get into action, but smoothing apply on them like on every other qubit. I think I agree about smoothing and measurements. When you apply a measurement-based scheme do you take the initial cluster state (or other required state) for granted or creating it is part of the process? And if you take it for granted what is your assumption regarding noise for this state?
Creating it can be part of the process. It only requires constant depth.
Aram, I am very interested in the following question. (And it is related to some little discussion with Mary-Beth Ruskai at the lecture).
Suppose that you create cluster state using a noisy bounded depth process with small noise rate. Is the resulting noisy cluster state still supports measurement-based computing. (There are fault tolerance versions for measurements-based computing but I ask about this specific case.)
I think those are the same question, and the answer is “yes.”
I’m not sure what the right reference is, but here’s one possibility:
http://arxiv.org/abs/quant-ph/0611273
Gil,
Suppose Alice and Bob share some EPR pairs. Alice starts doing a quantum computation that is undergoing SLE noise, and halfway through her computation, she teleports the whole state of the quantum computer to Bob, who continues the quantum computation. What happens?
I think some of the possible answers are:
1. the SLE noise starts up on Bob’s qubits as soon as Alice makes the teleportation measurement on her end.
2. the SLE noise starts up on Bob’s qubits as soon as he received the classical bits involved in teleportation and applies the corresponding unitary change to his halves of the EPR pairs.
3. the SLE noise does not pass through the teleportation procedure.
I should warn you that no matter what your answer, it will either lead to fault-tolerant quantum computation despite SLE noise, or something that looks very much like a paradox.
Another fairly concrete mathematical question:
Aram: “I suspect there is no mathematically consistent way to define evolution that is described by SLE for all Hilbert spaces and all time intervals, apart from trivial cases, such as having no noise and no interaction.” I think that this is an excellent challenge, and I made several times a similar challenge myself. “Having a model with many-scales forms of smoothing when you consider both different time scales and different Hilbert-subspaces may be possible and quite interesting!”
We need to describe a (possibly infinite-dimensional) Hilbert space and a quantum evolution on time intervel (-∞, ∞) so that for every window consisting of time interval and a finite dimensional Hilbert space, if the induced evolution is nearly unitary then it is approximately smooth. (Perhaps even with rate of noise lower-bounded by a noncommutativity measure of the evolution.) On first sight this looks like a concrete interesting mathematical question. My guess contrary to Aram’s is that there are non-trivial such examples.
Loopholes regarding SLE for non unitary evolutions.
SLE is offered as a theory of Lindbladians perturbation for unitary evolutions in nature, but we have two potential loopholes in the SLE idea when we try to extend it to non-unitary evolutions. (I agree with Aram that in principle we should be able to extend it.)
One loophole based on Peter’s example is to consider a quantum evolution on a certain array of qubits (it need not be a single qubit) and then restart the computation. Anyway you look at it, the smoothing should not “pass” the restart step.
The other loophole is Peter’s recent teleportation example where Bob continues a computation by Alice on a new array of qubits. If the teleportation process itself is noiseless then I suppose that we want to see the combined computation as representing a way to carry the original one and the SLE conjecture should apply.
Actually I would be interested to see, Peter, your analysis of the three cases you mentioned, and, in particular, the paradoxical consequences.
Right now I don’t have a response to these two loopholes. I can think about two ways to go about them. First to consider the system as a large unitary system and see what an SLE noise tells us about the large system. The other is to think about them in the context of present-day experimental physics. Since we don’t have any quantum fault-tolerance, present day quantum unitary systems should be well approximated by their own smoothing.
One word about paradoxical consequence. We saw that the very mundane assumption that (if you are willing to spare the time) every unitary computational process can be repeated several times in a row, together with SLE leads to a paradoxical consequence. This is because in a world without quantum fault-tolerance (or even in a world before quantum fault-tolerance) not every unitary computational process can be repeated several times in a row.
If the global evolution is unitary, then there is no “noise” (I use scare quotes, because I believe the division of Hamiltonian/Lindblad terms into intended/unintended or control/noise is itself ill-defined, and that this objection still has not been satisfactorily answered, probably because it can’t be). In this case, smoothing has no effect.
But on subsystems, evolution is not unitary, and smoothing has an effect. Thus, we _generically_ have incompatibility. For things to be compatible, stars have to align in implausible ways. Moreover, it seems that things are compatible only when the SLE has no effect.
As for the repeatability of unitary processes, our point is that if we have the ability to apply a unitary (really nearly-unitary) operation to a system once, then usually we can do it again and again, if we don’t mind using more electricity. When you say that without fault-tolerance we cannot repeat unitary evolutions, I think this confuses whether we can repeatedly apply a unitary process with whether we can protect quantum information. Without fault-tolerance, we (probably) can’t protect quantum information (although this sentence is deeply problematic, because “without fault-tolerance” is not, and probably cannot be, a mathematically precise statement). But we can certainly repeatedly apply unitary evolutions. e.g. we might apply a laser for a nanosecond to rotate the state of an atom. The fact that noise is present doesn’t prevent us for leaving this laser on for a millisecond – or a month – if we want. I don’t understand the justification for your assertions to the contrary (“not every unitary computational process can be repeated”) even if you were to assume SLE.
Hi Gil,
Here are the problems I came up with for these three possibilities:
1. the SLE noise starts up on Bob’s qubits as soon as Alice makes the teleportation measurement on her end.
Regular depolarizing noise on two qubits means that |00> will go to either |01> or |10> but is unlikely to go to |11> directly. If you apply a CNOT gate to these two qubits, then the resulting SLE noise is that |00> will go |01> or |11> but is unlikely to go to |10> directly. Now, suppose Alice teleports the first qubit to Bob and the second qubit to Charlie. Then, after Alice’s teleportation measurement, whenever Bob’s qubit flips, Charlie’s must almost always flip simultaneously. But simultaneity isn’t even defined for spatially separated qubits (see relativity). Of course, you can only observe the qubits flipping post facto by doing state tomography on Bob and Charlie’s states, and then using postconditioning on the classical bits Alice sends Bob and Charlie. But if you do this, you should be able to tell exactly what quantum process is. And given relativity theory, I don’t see how this process can be uniquely defined.
2. the SLE noise starts up on Bob’s qubits as soon as he received the classical bits involved in teleportation and applies the corresponding unitary change to his halves of the EPR pairs.
Maybe my objection to (1) still applies, but here is another objection. For one of the outcomes of Alice’s measurement, Bob’s unitary correction to his half of the EPR pair is to do nothing. It is impossible to tell when Bob applies this identity gate to his half.
3. the SLE noise does not pass through the teleportation procedure.
The problem here is that, if you can erase SLE noise by using teleportation, you can do fault-tolerant quantum computation by repeatedly erasing the SLE noise.
(2) has the further problem that the classical message has to somehow be tied to the quantum state. But we could pass it through any number of intermediaries, or generally have it take an arbitrarily convoluted path from Alice to Bob.
(3) has the further problem that the distinction between measuring a qubit and performing a unitary CNOT on it is not well-defined. And in the latter case, SLE noise spreads.
Hi guys,
Let me try to summarize Peter’s teleportation argument.
First I recall my conjecture: In every realistic (approximately unitary) system the unitary evolution is subject to smoothed noise. (That can come in addition to other forms of noise.) Smoothed noise is defined as being well approximated by an SLE on every time scale. (And SLE is defined via a truncated Gaussian kernel of some window of length ε; the quality of the approximation in “well-approximated” depends on ε. The notion of approximation was also indicated and discussed above.)
Now we consider a computation with m qubits that at some intermediate time the state is teleported from Alice to Bob and the computation continues on Bob’s side. We can regard the situation as a system on 2m qubits (m pairs) and we want to check if the conjecture on the 2m-qubit system implies the conjecture on the teleported computation on m qubits. (Actually since the computation involves some measurements it looks that we need to enlarge the system even further, perhaps to 3m qubits, so that the large system is unitary +noise.)
Your argument is that there are three alternatives. Alternative 3) is that the teleported system violates the conjecture and your conclusion is that this will enable fault-tolerance quantum computing. The case that the teleported evolution obeys the conjecture is divited further to alternatives 1) and 2), and for them you present various conflicts with special relativity and some other things.
In more details, the three alternatives you consider are:
1. the SLE noise (for the teleported system) starts up on Bob’s qubits as soon as Alice makes the teleportation measurement on her end.
2. the SLE noise (for the teleported system) starts up on Bob’s qubits as soon as he received the classical bits involved in teleportation and applies the corresponding unitary change to his halves of the EPR pairs.
3. the SLE noise does not pass through the teleportation procedure.
Is this a good summary? Do you feel confident about this argument? This is quite interesting! Let’s think about it!
Certainly, I would expect the SLE conjecture to apply to the teleported system. The best would be if assuming it for the large system allows you to derive it for the teleported system. But you seem to say that the idea that the teleported system satisfies the SLE conjecture is self-contradictory based on the issue of “when the SLE starts?” This, I find quite surprising.
Hi Gil,
This is exactly my argument. I think it’s clear the SLE noise cannot be passed by classical bits. What if Bob uses random bits instead of Alice’s? They’ll match some fraction of the time, and I think you have to assume that the physics doesn’t care whether Bob uses random bits instead of Alice’s measured bits. This means random bits have to carry the SLE noise whenever they match Alice’s bits, which seems absurd.
If the noise is passed by the quantum bits, you run into contradictions with simultaneity and relativity: if you say the noise starts on Bob’s qubits as soon as Alice’s qubits are measured, then you have to assign a meaning to “simultaneous” over a spacelike interval, which violates the fundamental tenets of relativity theory.
I suppose you could also assume that the SLE noise goes backwards in time and is transmitted via the original EPR pair, but that is disturbing to me as well (I don’t like things that go backwards in time, and I am certain the EPR pair should be the least noisy at the time it is created, which means I don’t see how noise could be transmitted through it).
Dear Peter,
The problem is that I don’t even understand the concepts of “when does the SLE start on Bob’s side?” or “what carries the SLE?”
You have this system with m pairs of qubits and you can define an evolution on m qubits where in the middle you teleport the data from Alice to Bob. I look at the teleported noisy evolution. (This is a very baby-version of quantum systems on protected subspaces.)
Suppose, for example, that m=1 and that every qubit weather own by Bob or by Alice has a small probability to be depolarized. In the teleported system again the single qubit has a small probability to be depolarized at all times (or most times). This is an SLE noise so, in this case, the teleported system obeys the conjecture. Yet, I don’t even understand the notion of “How the SLE noise is passed” and “when the SLE noise starts.” Or suppose that the entire evolution is of depth ten. Then the teleported system, again of depth ten, satisfies the SLE conjecture. And again, I don’t understand the question about “where does the SLE start on Bob side” and “how is the SLE noise passed.” (Since the conjecture is about approximations, I don’t see how the question “when does the SLE noise start” is important, but, first of all, I don’t understand what it means.) It seems that the intuition of you and Aram is based on some physical smoothing process that is actually taking place.
Anyway, maybe I miss here something.
Hi Gil,
Alice and Bob start with EPR pairs which have been created but had nothing done to them. If I understand your conjecture, they are relatively noiseless, and only undergoing the decoherence that would have been predicted by standard quantum mechanics. Now, Alice takes some qubits in the middle of a quantum computation. They are undergoing SLE decoherence, which is different, and larger than, the decoherence that is predicted by normal standard quantum mechanics. Using the EPR pairs, she teleports the quantum computation to Bob.
When do Bob’s qubits start undergoing this extra SLE decoherence?
Maybe I should explain more carefully. Let’s repeat the experiment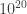
times, each time with fresh qubits. Now, we can measure the state of the system at every stage, and figure out exactly how much decoherence is going on. That is, we can calculate the unitary evolution and experimentally find 
at every step.
I assume from what you have said so far is that the EPR pairs shared by Alice and Bob are going to behave in the way predicted by standard quantum mechanics before Alice has done anything to them. However, once Alice has teleported the quantum state from the quantum computation to Bob, this quantum state (which is the same state that Alice had in the middle of her computation) must undergo decoherence that is approximated by a smoothed Lindblad equation. This is not what standard quantum mechanics says.
Teleportation consists of three steps.
(1) Alice measures the joint state of the quantum computer and the EPR pairs.
(2) Alice transmits the classical results of this measurement to Bob.
(3) Bob applies a unitary operation that depends on the result of this measurement to his EPR pairs, at which point he has (up to errors caused by imprecision in the teleportation process) exactly the same state that Alice had when she made the measurement.
We know from your conjecture that the evolution of the logical qubits is going to have to be approximately a smoothed Lindblad evolution. However, during the teleportation process, the state of the quantum computation isn’t really described by either the classical bits being sent by Alice, or by Bob’s qubits. Do we (1) use Alice’s measurement results and Bob’s qubits to infer a logical state of the computation during the time that the measurement results are being sent to Bob, in which case the decoherence undergone by Bob’s qubits must match some SLE during this time. Or (2) do we just require
to be approximately smoothed from the point where Bob applies the unitary operation depending on the results of Alice’s measurement to his half of the EPR pairs, and assume that Bob’s qubits undergo the decoherence predicted by standard quantum mechanics before that time. Or (3) something else entirely.
Let me briefly relate to the one before last comment.
“They are undergoing SLE decoherence, which is different, and larger than, the decoherence that is predicted by normal standard quantum mechanics.”
Usually, the SLE decoherence is neither different nor larger than the decoherence predicted by normal standard noise models. As I mentioned in my papers, I regard the SLE as just a different harmless bookkeeping that makes little difference unless the system involves quantum-fault-tolerance. It is just that when the system demonstrates quantum fault-tolerance the different bookkeeping of the SLE gets out of control. Perhaps the most relevant paper is “when noise accumulates,” linked here. Embarrassingly, I noticed that I devoted subsection 7.2 to discuss an example very similar to Peter’s but forgot about it. (It is true that I considered quantum systems which are approximately unitary and where the state of the system is close to being pure at all times.)
Again, what is the idea? Let’s think discrete time and suppose that at time t you are hit by some noise E_t. What do I say? that we take some small part of E_t, allow the evolution act on it for a small time, and pretend that it appeared a little later with the same effect it would have had. (Or do the same backward in time.) So the idea is: if the system does not represent quantum fault-tolerance, such a smooth noise will be a small perturbation of the original E_t. Just representing a mundane different bookkeeping.
In the Alice/Bob case with standard noise models, again, usually (perhaps after ignoring some ingredient of the noise) the smoothed noise will be quite close to the noise before smoothing – not different or distinct or larger.
Sections 7.2 and 7.3 of “When Noise Accumulates” sure make it seem as though SLE is untenable.
Hi Gil,
So you’re saying that the SLE conjecture noise is completely indistinguishable from ordinary quantum noise unless there is some quantum computation going on, in which case it suddenly stops it from working. I can’t reconcile that with your equation, which does not seem to describe a lot of forms of quantum noise.
My argument does not rely on the SLE noise being larger than the standard quantum computing noise, just its being different. And the argument is that if you teleport the state in the middle of a computation, there must be a point when the noise on Bob’s state changes from noise consistent with smoothing Bob’s half of the EPR pairs to noise consistent with smoothing on the computational subspace. And whatever you pick for this instant is incompatible either with relativity or with the fact that doing nothing to Bob’s state shouldn’t change the noise on it.
But if you claim that SLE noise is completely indistinguishable from standard quantum noise unless you’re doing a quantum computation, my argument falls apart. However, this claim also makes SLE noise completely indistinguishable from magic. If the SLE noise is different for states undergoing quantum computation, it has to be distinguishable on regular quantum states. Otherwise, Nature would have to be able to tell whether you are doing a quantum computation.
Aram: “Sections 7.2 and 7.3 of “When Noise Accumulates” sure make it seem as though SLE is untenable.”
These sections show that you cannot assume that the noise is described (approximately) by an SLE (which was my fantasy) but rather the conjecture should be that the noise contains a component approximated by an SLE. In our debate I thought that adding an atom at 0 for K(x) suffices to move back to the fantasy version but our current time-scaling discussion convinced me that this atom is not useful and we should go back to the conjecture that the noise contains a component well-approximated by an SLE. This version should suffice to exclude FTQC.
“My argument does not rely on the SLE noise being larger than the standard quantum computing noise, just its being different.”
In the teleportation example, the SLE conjecture should apply both when you restrict yourself to Bob’s part, and when you restrict yourself to Alice’s part, and when you consider the computational subspace. The SLE conjecture does not specify the noise but rather gives constraints on the noise. Indeed in various cases these restrictions are different than the standard assumptions regarding noisy quantum computers. In your example you have several constraints simultaneously and they all should be satisfied. (And, as I said, it will be interesting to derive the constraints for computational subspaces from the constraints for the system of “physical” qubits.)
“And the argument is that if you teleport the state in the middle of a computation, there must be a point when the noise on Bob’s state changes from noise consistent with smoothing Bob’s half of the EPR pairs to noise consistent with smoothing on the computational subspace. And whatever you pick for this instant is incompatible either with relativity or with the fact that doing nothing to Bob’s state shouldn’t change the noise on it.”
I do not think that this argument is correct. The noise on Bob’s state should be consistent both with smoothing on Bob’s part and with smoothing on the computational subspace. There is no transition time and certainly there is no “instant.”
Let me give examples where the SLE conjecture/intuition tells something different than what people expect using insights coming from standard noise models. You try to create a surface code. (So people are actually trying to do it experimentally.) People sometimes expect based on ordinary noise models that you will be able to create very robust codewords subject to some independent noise on the computational basis. What I expect is that you will necessarily have a mixture of a cloud of codewords and in addition also some independent noise on the computational basis. Similar distinctions between the expectations coming from SLE and those coming from standard noise models can be made for fractional Hall effects, highly-stable qubits based on pairs of anyons that you moved far-apart, and Bose-Eisntein condensation ( in the later case the SLE expectation agrees with what people do expect for BE condensation, but for other reasons.)
It is correct that people can reach my conclusions without directly referring to the SLE formulation, but simply by carefully thinking about what they can expect from a quantum process subject to standard noise models which does not exhibit genuine quantum computing/quantum fault-tolerance. This was my argument regarding topological quantum computing. (See the underlying slide in the post.)
Hi Gil,
in your equation. I assume this means you think the computational subspace exists during the teleportation of Alice’s qubits to Bob. But by relativity, there is no one time variable 
which can be defined consistently on Alice’s system and Bob’s systen. Should the evolution be close to smoothed for all possible definitions of this time variable (i.e., in all reference frames)? Is that even possible?
During the time that Alice is sending the classical information to Bob, what is the “computational subspace” that you have to smooth over? You have the unitary
Dear Peter, Generally speaking, my conjecture is based on a model that abstracts away much of the physical situation, and it should apply for every implementation which fills up (realistically) these missing parts. (Of course, also the standard models for noisy quantum computers abstract away much of the physics.) The conjecture is formulated for approximately unitary evolutions where I mainly thought about situations where the state is nearly pure at all times, but it should be possible to extend it to non-unitary cases. The conjecture should apply for every “protected” subsystems. (There is even hope that it can be derived for protected subsystems from an appropriate version applied just for the “physical” non-unitary systems used in quantum fault-tolerance.)
If the same physical system gives different ways to look at a certain subsystem, (e.g. referring to the time) then I suppose that the conjecture should apply to all of them. So if indeed in a situation that a computation is starting on Alice’s side and continuing on Bob’s side there are different ways to look at time for the protected evolution then the conjecture should apply to all of these ways.
One thing that we discussed earlier can be relevant. If you have a class of systems which are approximately smoothed and if you enlarge the class by allowing to insert the identity as the unitary part for a period of time at the end of an evolution or, as a matter of fact, also in the middle, than the smoothing conjecture carries over to the larger class of evolutions. (The identity periods can be as large as you want.) This might be relevant to the issue you raised that the protected teleported evolution can be described time-wised in different ways. But I don’t know if this argument or a related one settle the issue you raised completely.
Hi guys,
Peter raised some issues of special relativity so let me mention a couple things (possibly naive or even stupid) that I am curious about.
1) We are used to think about QM and special relativity as distinct developments in very early 20th century physics, and on these theories, on their basic level, as fairly orthogonal. So textbooks (and popular books) analyse interesting quantum phenomena like Schrödinger cat that have nothing to do with relativity, or issues of special relativity like the twin “paradox” that has nothing to do with QM. My naive impression, However, is that in “real life” we witness quantum mechanical phenomena and special relativity phenomena in the same physical regimes. Do you know if this impression has some truth to it, and, if true, what are the reasons for that?
In particular, is it the case that a system realizing a Schrödinger cat will necessarily manifest substantial effects of special relativity, and a system demonstrating the high speed twins, will necessarily manifest substantial quantum effects?
2) Suppose that we have a large number of particles moving apart and towards each others in speeds close to the speed of light. Special relativity leads to some subtle issues regarding the internal clocks of these particles, and how are they being synchronized. Does this suggest that (in the regime were special relativity effects are substantial) it will be, in some cases, difficult, or even impossible in principle, (for us or for nature) to mutually control the interactions between these large number of particles? (Also can we expect that the trajectories of each of these particles will actually be superposition of various scheduling?)
My own work (like most works on quantum fault-tolerance) completely disregard special relativity. (In fact, my models are blind to any geometry.) I don’t remember that issues of (basic) special relativity were much discussed in the long discussion with Aram over GLL. Questions regarding quantum field theories, that unify QM and special relativity were raised in quite a few comments. Perturbation methods in these theories are connected to noise models for quantum computers, and also the whole idea that quantum computers have superior computational power came from the experience in computations coming from quantum field theory.
Finally, I think that Peter’s comment regarding time-smoothing, teleportation and special relativity, is certainly something to take a note at, and the example of a computation starting with Alice and ending with Bob is very basic. But I cannot really see, how this example is an argument against my conjecture. If the issue is how to relate the conjecture applied to Bob’s actual time with the conjecture applied to the protected teleported evolution (which has its on clock) then this, I think, will reflect that the class of smoothed-time systems is very robust to changes of the kernel K(x).
Hi Gil,
One nice example which combines bits of relativity with some bits of QM is the Conway&Kochen “Free will theorem”
Click to access rtx090200226p.pdf
A standard example where one uses both QM and relativity is of course the EPR-paradox
http://en.wikipedia.org/wiki/EPR_paradox
1) special relativity and QM certainly can reduce to the classical limit in very different regimes. For example, special relativity often becomes noticeable when a particle is moving close to the speed of light, whereas QM often is noticeable when a particle’s de Broglie wavelength (which scales as the INVERSE of velocity) is large relative to other length scales in a system. On the other hand, there are plenty of systems where both are important, like particle accelerators. One common system is the Hydrogen atom, where you can calculate most of what’s going on by ignoring special relativity, but where relativistic effects give you a roughly 1% correction to the energies. In many systems relevant to QM, you can treat relativity phenomenologically, by just treating it as something that shifts some energy levels, without qualitatively changing what’s going on.
In all of our mentions of relativity (ditto for Klas’s reference to the EPR paradox), we are using only one fact, which is that if you can signal at large distances faster than the speed of light (aka “instantaneously”) then this ability is equivalent to the ability to signal backwards in time. Since the latter leads to paradoxes, whenver we say “relativity” this is shorthand for “The no-instantaneous signaling theorem”.
2) In this case, the acceleration will cause (via the Unruh effect) each particle to experience noise. This effect is pretty small (see the wikipedia article on it for an example). Also, if two systems are accelerating away from each other at a constant rate and are communicating by exchanging particles at the speed of light, then as they get farther apart, it will limit the number of messages they can exchange.
In general, though, there is no problem controlling these things and getting them to do quantum things. I can say that with some confidence because we do it all the time with photons and stationary atoms, and of course photons move at the speed of light. 🙂
Usually, when you combine quantum mechanics and relativity you are forced to use quantum field theory. But there are situations in quantum computing where you can learn stuff by using plain quantum mechanics and the fact that you cannot transmit information faster than light to draw conclusions.
A possibly relevant argument is as follows. Suppose you have imperfect EPR pairs, and you teleport the computation from Alice to Bob. You can deduce that any SLE noise found in Bob’s state before the news of Alice’s measurement has reached him must be undetectable by Bob. With perfect EPR pairs, this is automatic, but with EPR pairs in the state
, where $\alpha = \frac{1}{2} + \epsilon$, I think Bob might be able to measure the noise by statistically testing a large number of noisy EPR pairs. For example, if you have depolarizing noise, and Alice applies a CNOT gate to her halves of the EPR pairs before teleporting the state of the system to Bob, Bob’s SLE noise is correlated between his halves of the EPR pairs. (Question to Gil: is this statistically detectable? If not, why not?)
So now, we get two possibilities:
, where 
is the distance from Alice to Bob and 
is the speed of light. I don’t see how this is compatible with Gil’s view that his model is able to abstract away the “physical situation”, as this seems to give different behavior depending on how far apart Alice and Bob are.
1) the SLE noise induced by teleportation through imperfect EPR pairs is undetectable by Bob. This introduces strong constraints on the possible form of any SLE noise.
2) the SLE noise induced by teleportation through imperfect EPR pairs is detectable by Bob. This means that for information not to be transmissible faster than light, the SLE noise cannot show up before time
Peter, for me to better understand your argument I need to understand what’s special here with SLE noise? What happens when you replace “SLE noise” e.g. by “depolarizing noise.”
Gil,
You described earlier your idea as “we take some small part of E_t, allow the evolution to act on it for a small time, and pretend that it appeared a little later with the same effect it would have had.” When you take a small amount of depolarizing noise, allow a CNOT gate to act on it, and pretend it appears a little later, it turns into correlated noise. If it moves from Alice to Bob via the teleportation step (which it has to, since the computational subspace moves from Alice to Bob), Bob should be seeing some correlated noise along with the depolarizing noise that regular quantum mechanics predicts.
My question is: can Bob perform an experiment to measure this correlated noise? If you use perfect EPR pairs to teleport, the answer is “no”. But if you use slightly imperfect EPR pairs (which are all imperfect in the same way), I don’t see why the answer shouldn’t be “yes”.
If Bob starts with imperfect EPR pairs, he can definitely measure the effects of plain depolarizing noise on his halves of the EPR pairs. The question is whether he can make a measurement which distinguishes correlated noise from plain depolarizing noise. Since correlated noise destroys quantum computation, and plain depolarizing noise doesn’t, you would think their effects would be statistically distinguishable using some measurement. And if I take the naive form I would expect to see of the correlated noise, the effects are indeed distinguishable.
But maybe there’s some complicated form of correlated noise which is able to hide itself perfectly in depolarizing noise, and the only way to detect it is to wait until after Bob gets the classical value of the measurement from Alice. Offhand, I can’t prove that such a way of hiding SLE noise doesn’t exist. But I am willing to bet that right now, you can’t prove that such a way of hiding SLE noise exists.
Peter, let me see if the following scenario captures your teleportation point without involving special relativity or teleportation. Suppose that we run the whole process with Bob, but that I allow to “freeze” the entire process for a certain amount of time (corresponding to d/c in your example.) You may ask
a) Should the SLE conjecture apply w.r.t. the real physical time?
b) Should the SLE conjecture apply w.r.t. the “protected” process where the freezed time is taken out?
c) If the answers to both a) and b) are yes doesn’t it impose too strong conditions on the SLE noise?
d) If the answer for a) is yes, since the length of the freezed time make a different for the description of the system, how can I claim that my model abstracts much of the physics away.
Assuming freezing is possible (that I am willing to take for granted) do these four questions capture all the teleportation/special relativity critique or there is some additional ingredient for the teleportation description that is not captured here?
Hi Gil,
I think your scenario covers it fairly well.
Actually, thinking about this more, I’m not sure I agree with this simplification. In teleportation with imperfect EPR pairs “breaks” the state into two seemingly inseparable “pieces”. One piece belongs to Bob, and corresponds to the imperfections in the EPR pairs, and if you do anything but standard decoherence to this piece you can transmit information faster than light. The other piece is the computational subspace, and this is the piece that is teleported from Alice to Bob and where the computation takes place. The imperfect EPR pairs introduce errors into the computation, but you can assume they are small enough that standard quantum error correction fixes them.
So what you want SLE noise to do is introduce error into the computational subspace and not into Bob’s piece.
Hi Peter:
1) Suppose we have a unitary evolution, and an SLE system based on it. It may be useful to note two extreme cases.
a) Every noise is SLE with respect to the identity evolution,
b) “Global” depolarizing noise of the kind that with probability t the state is changed to the maximum entropy state (for the entire Hilbert space) is an SLE with respect to every unitary evolution.
So the SLE conjecture, which asserts that (in realistic systems) we can find a component of the noise which is approximately an SLE does not necessarily introduced very exotic noise, but rather eliminate some exotic unitary evolutions. As I often said, when you have standard noisy system which does not employ quantum fault-tolerance then I expect that the SLE conjecture is satisfied.
2) Regading my simplified version of the teleportation argument based on freezing. My conjecture is that both a) and b) are satisfied. For how this is possible (question d) ) there is a relevant mathematical property that we discussed before: If the SLE conjecture holds for a class of quantum systems then it will continue to hold uniformly for the larger class of systems obtained by inserting freezing intervals.
3) There is a crucial element to my thinking which may be responsible to some of our differences. I talk all along about a special purpose device which carries a specific quantum evolution. It seems that Peter’s thinking is based on a general purpose device or at least on a many-purpose device.
If you wish to perform a certain quantum evolution then you will build a special device and for this device my conjecture asserts that the error-model will include a component which satisfies the SLE conjecture. You may think about the quantum evolution and the derived properties of the noise as “wired in” to the specific situation. It is not that we have a controlled quantum evolution and that miraculously the noise adapts itself to the evolution, and there is no physical “smoothing” that is taken place.
4) I think that there can be another mathematical way to present the SLE conjecture. Namely that for a noisy quantum evolution the correlation between E_t and U_{s,t}E_s is positive and bounded away from zero. I agree that lower bound for the correlation (which represent the smoothing-scale) as well as a lower bound for the magnitude of errors themselves can be read from the evolution itself.
What is the difference between a single-purpose and a many-purpose device? Every physics experiment I know of has “dials” you can adjust, so none of them are designed to give a single quantum evolution. Why should this matter?
Hi Gil,
About your claim “when you have standard noisy system which does not employ quantum fault-tolerance then I expect that the SLE conjecture is satisfied.” I still haven’t been convinced that you’ve dealt with my first example.
You have dephasing noise, and you apply a gate which rotates by an angle of R_θ. Now what happens is that the SLE conjecture says that you can imagine a little piece of the dephasing noise E_t that happened before the gate and consider that it instead happened after the gate, and vice versa. But the noise before the gate does not commute with the noise after the gate, and when you combine them they make depolarizing noise which isn’t predicted by standard quantum mechanics..
This is a realistic system (at least in that there are systems where the dephasing noise is orders of magnitude larger than the depolarizing noise), and I don’t see how the SLE conjecture agrees with standard quantum mechanics here. While if you use your distance measure between the two noise records in the system, it’s small, I don’t see that this really makes much of a difference. The SLE prediction is different from the standard quantum mechanics prediction, and if the proportion of SLE noise was at all large, the difference could be detectable by measurements if an experiment was done.
Peter, The SLE conjecture only says that for a realistic system there will be a noise-component which is approximated (in the mathematical sense I described) by an SLE. In your example (when you apply one or a few rotations), the system itself is well approximated (in my sense) by an SLE.
(On top of this, there are cases where the SLE noise can vanish. This has to do with a non-commutativity measure for the projections in a certain algebra of operators. So if you dephase your system completely so it collapses to a classical system you can assume the SLE noise (or its effect) to be 0.)
Hi Gil,
Why should I care about the system being well-approximated in your sense if the evolution predicted by SLE noise differs from experiment?
Peter: “Why should I care about the system being well-approximated in your sense if the evolution predicted by SLE noise differs from experiment?”
Haa that’s a good question, and it reminds me a story from my youth. Many years ago there was a top-secret military base in Israel and in order to get in you needed a photo ID card that only few people after much scrutiny could get. One day, somebody approached the gate of the base. “Do you have an ID card” he was asked. No, I forgot it,” he replied, and then he took from his wallet a picture and showed the soldier in the gate, “you see, this is me!“. The picture matched the face perfectly so the soldier let him in.
The SLE test is proposed as the identity card. If you don’t pass the test you should not get in. Of course, your face are better described by what they are compared to the picture on the ID.
The SLE test will show that many unitary evolutions are unrealistic. In many cases it will give important predictions for systems approximating unitary evolutions and pure states that can be realized. (I have a whole array of conjectures regarding these predictions.)
Finally, unlike the guy’s face the top-secret army base your example was just a picture that you have drawn yourself. You wrote: “This is a realistic system (at least in that there are systems where the dephasing noise is orders of magnitude larger than the depolarizing noise),”
Let me, once, go on a limb and predict (based on the SLE intuition, but not on the formal SLE conjectures) that unlike the systems you referred to, and your example, every viable attempt to realize a single-qubit general dynamics is subject to a substantial amount of depolarizing noise.
The problem with all of this is that very good single qubits DO exist. Atomic orbitals, photon polarizations, electron spins, nuclear spins, superconducting two-well systems, etc. These have been well-studied for decades, and in some cases, even before the emergence of quantum mechanics. And the interaction between experimentalist-imposed unitaries and naturally-generated noise that SLE posits has never been seen. Another way to say this is that most of our experience with single qubits would be considered “unrealistic” according to the SLE filter, unless you say that in each case so little noise was smoothed that we couldn’t see it.
Hi Gil,
If you apply the rotation by R_θ repeatedly, then the system disagrees with the predictions of standard quantum mechanics by both your measure and the more standard measure of having different probabilities of experimental outcomes.
I would also say that if you did this experiment, the amount of depolarizing noise would be no more than could be accounted for by standard quantum mechanics and experimental error. You will never get any depolarizing noise more than can be accounted by standard quantum mechanics, and that can be orders of magnitude smaller than the dephasing noise.
Aram, The SLE test does not exclude one qubit-dynamics and the scale for the smoothing is the same as the scale for the noise. (The issue of full or partial restarts seems important and it should indeed be addressed: we should not expect smoothing to span over times when the quantum information itself is lost.) Peter, if you apply various rotations to a single qubit then, (as long as you do not decohere and do not restart,) the SLE approximation works fine when the scale of the smoothing is the same as the scale for the noise. BTW, if you keep applying the same rotation then this is precisely a case where the SLE-noise can vanish. Of course, any given quantum system is better described by itself compared to the filtered SLE description, and remember that I do allow that the SLE noise will only be a component in the overall noise. (While the extensions to non unitary evolutions and non (approximately) pure states is important, I propose to think also on the regime that I was interested the most. You have a noisy system which is approximately unitary, the state is approximately pure, and you wish to draw a picture of decoherence for systems that do not invoke quantum fault-tolerance so that the noise accumulates.)
Hi Gil,
What do you mean by “the scale of the smoothing is the same as the scale for the noise”?
Dear Peter, What I meant is simply that the smoothing window is some ε times a computer cycle. (So if the noise in each computer cycle is t, so it can keep you alive for O(1/t) steps, the smoothing window is ε times t times the computation interval.)
“A computer cycle” = the time for one gate?
t is dimensionless?
So if gate time is X and decoherence time is Y, then t=X/Y?
In this notation, you are saying the smoothing time is eps * X * t = eps * X^2 / Y?
GK: Aram, the smoothing time is eps*X.
What do you mean by computational interval?
Hi Aram:
I think Gil means that the smoothing window should be roughly the decoherence time. Can we still do quantum computation in this SLE regime?
Let’s consider a noisy quantum computation with a single qubit so that the computation is a unitary evolution described by a sequence of unitary gates, and the noise is described by a POVM measurement. (There are more general single qubit evolutions but let’s not worry about them now.) Let’s take the “computation interval” as the interval where the entropy of our noisy state is less than 0.5 (say). The case of a single qubit is actually a little “role model” for what we mean by “the noise accumulates,” so indeed it can be useful to use it to tune the various definitions. Regardless of what the noise is, if the smooth window is ε times the computer cycle then this system is approximately an SLE. As I said, I would expect (and this is not that surprising either) that in all viable attempts to realize single-qubit quantum computation we will witness a depolarizing noise which is an SLE for a much larger smoothing window – the entire computational time.
If the noise rate for one computer cycle is t, then as the noise accumulates you can carry on (1/t) computation cycles. The common belief is that t is bounded below by some constant which reflects our experimental/engineering abilities, but is bounded away from 0. The question on how the noise rate depends on (or, more precisely, bounded below by) the quantum evolution, and specifically how the rate scales up (if it scales up) with the number of qubits is, of course, very interesting.
Does this mean that you conjecture that quantum error correction hardly helps at all: If the total number of noisy gates you can string together without error correction is $t$, then the total number of computational steps you can do is $Ct$ for some universal constant $C$?
Yes.
Peter: “What is the difference between a single-purpose and a many-purpose device? Every physics experiment I know of has “dials” you can adjust, so none of them are designed to give a single quantum evolution. Why should this matter?”
This question is truly at the heart of the matters. The models of noisy quantum computers takes for granted the scenario of a general-purpose machine and much of the intuition and arguments (even on this thread) regarding noisy quantum computation are derived from thinking about general-purpose devices. For example, it is agreed that the difficulty of the computational task has adversarial effects on the errors/noise/risk-of-failure. The model of general-purpose noisy quantum computation gives a very restricted form for the nature of this adversarial effect.
Of course, controlled (several-purpose) quantum devices are quite common, and once we understand the limitation of special-purpose quantum devices this will apply for controlled quantum devices. These limitations simply need to apply to any trajectory depending on the controls.
I don’t think we agree about there being an “adversarial” effect. I think that thinking about noise adversarially can be a way to bound things if we want to err on the pessimistic side, but I don’t think it’s an accurate description of nature. (Perhaps I have misinterpreted this point.)
Dear Aram, what I meant is only this: If you attempt to perform a more complicated task then the risk of failure is higher. If there is a better English word than “adverserial” for this I will be happy to use it.
Hi Gil,
I have been thinking about the cluster state computation and how SLE noise behaves with respect to teleportation, and it turns out these are very closely related. And it looks to me like something, that to me seems very disturbing, has to happen for the SLE conjecture to disrupt cluster state quantum computation.
Here is the scenario that disturbs me: We start with Alice sharing an entangled pair of qubits with Bob and another entangled pair of qubits with Charlie. Alice takes two of her own qubits, and performs a CNOT gate on them. After she has performed the CNOT gate, Alice’s two qubits are undergoing correlated SLE noise.
Alice now performs the measurement that would teleport one of these two qubits to Bob and the other to Charlie. At some point after she has performed this measurement, Bob’s half of his EPR pair and Charlie’s half of his EPR pair must start experiencing correlated SLE noise. This would not have happened if Alice had not performed the measurements. And this has to happen, even if Bob’s and Charlie’s qubits have never interacted with each other in their entire existence, and the only thing Bob and Charlie do with their halves of the EPR pair after producing them is measuring them.
Does this seem like a reasonable hypothesis to you? It doesn’t to me.
The reason this has to happen is that a cluster state computation essentially works by teleporting qubits.
Forgetting about cluster states, you can do computation solely by teleportation. The unitary gates can be accomplished by teleporting through EPR pairs which have had some rotation applied to them, and Controlled Z gates can be accomplished by teleporting through pairs of EPR pairs which have had a Controlled Z gate applied to them. The only unitaries you ever need apply are to EPR pairs which have just been produced, and which haven’t had anything done to them. It seems that these can’t experience SLE noise until one half of an EPR pair has undergone a joint measurement. And thus Alice’s measuring her halves of the EPR pairs must be what causes Bob’s half of the EPR pair to start undergoing joint decoherence with Charlie’s half of the EPR pair (since this is the only difference between EPR pairs which must be experiencing correlated SLE noise and EPR pairs which were just produced, and thus cannot be experiencing SLE noise).
To do quantum computation, the parties must also be communicating classical bits and using these to decide what unitary to perform on EPR pairs before teleporting with them. But having classical computation affect SLE noise seems even more unlikely than having the measurement of one half of an EPR pair induce SLE noise in the other half.
Indeed one of my conjectures asserts specifically that if you create an EPR pair the information-loss on the two qubits should be positively correlated. You have to assume it for gated pairs (namely when a 2-qubit gate apply to a pair of qubits), which is consistent with ordinary assumptions on gate-errors and with current experiments I suppose, and the conjecture asserts that this will hold for every EPR pair. (In fact the conjecture applies not only to EPR pairs but also to two qubits that become an EPR pair after a third quibit is measured.)
Let me try to understand you here, Peter. Are you claiming that by using teleportation we can create (today) an EPR pair of qubits so that the noise on them is uncorrelated? This will certainly violate my conjectures.
Hi Gil,
No, I’m not claiming that we can create an EPR pair of qubits so that the noise on them is not correlated. I am claiming that any correlated noise on an EPR pair of qubits is due to imperfections that were present at the time of the EPR pair’s creation.
Peter, let me see if I understand you. We created an EPR pair on Bob and Charlie’s qubits using teleportation. Are we in agreement that this EPR pair is subject to correlated noise, but we just try to figure out what is the cause of this noise?
I certainly agree that any EPR pair created in a course of a quantum computation, directly, or indirectly, is subject to correlated noise from the time it was created if not earlier.
Let’s take this in small steps.
Do you agree or disagree.
(1) If you have uncorrelated depolarizing noise on two qubits, and you put them both through a CNOT gate, the SLE conjecture now says that you will have correlated noise on both qubits, meaning that they both will flip simultaneously from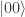
to 
or 
to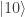 
(or vice versa) simultaneously. Meanwhile, the uncorrelated depolarizing noise will continue. This means the right qubit will be noisier than the left qubit, since the bit flips on the left qubit are transformed to bit flips on both qubit, but the bit flips on just the right qubit are left unchanged by the CNOT gate. (And the left qubit will be noisier than the right qubit in terms of phase flips.)
(2) After teleporting these two qubits to Bob and Charlie, there will still be correlated noise on both qubits, meaning they will still do these simultaneously bit flips. So now Charlie’s qubit will be noisier than Bob’s qubit.
Do you agree or disagree.
Peter, As I mentioned, the SLE conjecture says that in a realistic quantum system there will be a component of noise well approximated by SLE. As we discussed above this holds when there is a bounded number of gates. Another thing to remember is that if you have any evolution on a pair of qubits and your noise replace, with some small probability, the state with the maximum entropy state, then this is already an SLE noise (no matter what the unitary evolution is). So let me change “the SLE conjecture” in your formulation to “applying the smoothing operation” which is what you actually refer to.
(1) If you have uncorrelated depolarizing noise on two qubits, and you put them both through a CNOT gate, the
SLE conjectureapplying the smoothing operation now says that you will have correlated noise on both qubits,I certainly agree with this!
meaning that they both will flip simultaneously from
to 
or 
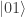to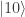 
(or vice versa) simultaneously. Meanwhile, the uncorrelated depolarizing noise will continue. This means the right qubit will be noisier than the left qubit, since the bit flips on the left qubit are transformed to bit flips on both qubit, but the bit flips on just the right qubit are left unchanged by the CNOT gate. (And the left qubit will be noisier than the right qubit in terms of phase flips.)
This looks OK.
(2) After teleporting these two qubits to Bob and Charlie, there will still be correlated noise on both qubits, meaning they will still do these simultaneously bit flips. So now Charlie’s qubit will be noisier than Bob’s qubit.
OK, if I understand you correctly the smoothed noise will be teleported to the pair of qubits of Bob and Charlie. This sounds very reasonable. What now?
Now, because computation can be done by teleportation measurements alone, the smoothed noise must appear in Bob’s and Charlie’s qubits as a result of the mere act of Alice’s measuring her qubits. This is action at a distance without the intervention of any apparent physical mechanism. It’s a much more radical modification of the laws of physics than just saying that there is some mechanism that somehow ensures that noise is smoothed across quantum gates.
Here I don’t get, you. Suppose that we actually run the experiment that you have described, just as you described it. What would you expect be the noise on the pair of entangled qubits of Bob and Charlie?
One more question: If Alice’s measurement is imperfect and instead of measuring with respect to the intended basis she measures with respect to a random SO(2) small rotation of it. Couldn’t this account for correlated noise on Bob and Charlie’s EPR pair?
Hi Gil,
You ask:
“If Alice’s measurement is imperfect and instead of measuring with respect to the intended basis she measures with respect to a random SO(2) small rotation of it. Couldn’t this account for correlated noise on Bob and Charlie’s EPR pair?”
This kind of imperfection can be modeled by a standard noisy gates, and can be shown to be fixable by standard fault-tolerant techniques.
Your SLE conjecture results in noise that I don’t see how to fix by standard fault-tolerant techniques. But if all the gates are performed by teleportation, the SLE conjecture (which says that the noise on one side of the teleportation gate is correlated with the noise on the other side of the teleportation gate in a way that isn’t fixable by standard fault-tolerant techniques) seems to require radical new physics.
To be more precise, in the SLE model of noise in a fault-tolerant quantum computer, the decoherence before the gate is smoothed across the gate, so noise before the teleportation is correlated with the noise after the teleportation gate. But there is no way for the noise that occurs after the teleportation gate to know about the noise before the teleportation gate, except through imperfections in Alice’s measurement, imperfections in the EPR pair, and imperfections in the state to be teleported before the measurement. All of these imperfections are modeled by the standard model of noise in quantum computers, where the noise on one gate is independent of the noise on another gate.
Peter, modeling noise using SLE deals with much more general quantum systems where you do not have “gates” and, in fact, you also do not get “qubits”. So the fact that when you restrict yourself to a scenario with qubits and gates you get similar phenomena for SLE to what you expect from the usual models but from different reasons is positive. Remember also that the SLE conjecture is about approximation where you are allowed to move your noise forward or backward in time, a little, so the concerns regarding precise timing that looks counter-intuitive or seem to “require radical new physics” are missing this point.
If you’re interested, quant-ph/9908010, by Gottesman and Chuang, is the paper giving the construction for computation by teleportation.
Let me try to make an analogy, which like any analogy is not perfect but I think it explains some crucial point.
Suppose that we consider two types of manned-transportation for our solar system:
General-purpose transportation system: you take a vehicle in some launching place close to your home, and you can fly it safely and quickly to any planet or moon in the solar system. You can either land on the planet and later take off from it, or observe it from near-by without landing and at the end you can land back in the same space-port you started or a different one.
Special-purpose transportation system: Every space travel requires a very specific plans and a very specific space vehicle.
(Of course, even the special-purpose vehicles will have plenty of controls and dials.)
Here, rather than talking about noise or errors we can talk about risk-analysis (which is pretty much the same thing). We want to examine the risk of failure of the entire system and its subsystems at every stage.
Let me say from the start that (unlike the case of quantum computers) I don’t see a reason to think that general-purpose solar-system transportation is not possible. Maybe it will be built some day. It is certainly quite difficult and well beyond the horizon. The point I want to make is that in order to examine the possibility of general-purpose transportation for the solar-system you may need to carefully understand the limitations of special-purpose transportation. A “threshold theorem” for a general-purpose architecture is certainly a useful thing to have. But if you will discover a principle that will limit the type of special-purpose solar-system transportation this will give you an opportunity to examine the possibility of a general-purpose transportation system (or, in other words, to examine the possibility that the threshold cannot be reached.)
Moreover, taking for granted the general-purpose scenario may lead to incorrect intuitions and arguments. Let us examine the following argument: In a manned mission to the moon, landing on the moon increases the risk in the early stages of the space-mission compared to a mission where you just circle the moon, because we need to carry with us an equipment for landing on and taking off from the moon.
This is quite reasonable. But if you take the general system scenario for granted you may raise the following objections:
1) How does nature know that we intend to land on the moon?
2) Suppose that Alice the astronaut flips a coin and decide at random if to land on the moon or just circle the moon just when she approaches the moon. How can this decision effects the risks in early stages of the mission? Isn’t it an example of signaling from the future to the past representing a radical modification of the laws of physics?
etc. etc.
These questions make perfect sense for the general purpose transportation model, but they make no sense for the special purpose model. Indeed for general purpose transformation your decision to land or not when you approach the moon does not increase the risk for your mission in the earlier stages. The causality structure for special-purpose machines is much different than that of general-purpose machines. I think that if you go over the arguments and wordings of your comments, Peter, you will realize that in many cases you implicitly assume the general-purpose scenario.
Going back to our case, the SLE conjecture does not represent any change in the laws of quantum physics. It is a different modeling of noisy quantum systems. When you look at the formula for SLE and think about general-purpose systems, it looks rather radical and you may regard it as expressing strange causality relations, strange non-linearities in tension with QM, and an environment that has long term memory for the past, and also for the future.
When you realize that these formulas represent modeling special-purpose devices, and that the unitary evolution as well as a smoothed noise are wired in the device that implement the computation, these concerns and intuitions no longer apply.
Hi Gil,
I guess one place where we differ is where you say that the SLE conjecture does not represent any change in the laws of quantum physics. The source of noise in quantum physics can generally be deduced from the laws of quantum physics, and I don’t see how the laws of quantum physics allow for SLE noise.
I guess you mean that the unitary evolution is the same with the SLE conjecture, but there’s a lot more to quantum physics than just unitary evolution.
“The source of noise in quantum physics can generally be deduced from the laws of quantum physics, and I don’t see how the laws of quantum physics allow for SLE noise.”
Peter, I think that here you go back to the implicit assumption of having a general purpose quantum device. There, modeling the noise (or risks of failure if you wish) can be fairly restricted. But if you want to express, in the language of quantum probability, the way your noise depends on the quantum device that carries the computation then the laws for the noise can be more involved.
Ok, let me try some agree/disagree questions with you guys:
1) You do not need to be skeptical about ice to investigate water and the physical distinctions between water and ice.
2) Quantum fault-tolerance represents a major phase transition for noisy quantum systems.
3) Phase transitions demonstrate important changes in physical properties that are worth studying. Like in other cases of phase transition it is important to formally study quantum systems that do not exhibit quantum fault-tolerance and to understand how they differ from quantum systems that exhibit quantum fault-tolerance.
4) Studying quantum systems without quantum fault-tolerance may lead to understanding for why quantum fault-tolerance is impossible.
Pingback: Dan Mostow on Haaretz and Other Updates | Combinatorics and more
I am very thankful to Peter and Aram for the many thoughtful and helpful remarks regarding smoothed Lindblad evolutions and to John and Klas for their participation and good contributions!
Peter Shor is a great hero in quantum computation and quantum information and, in particular, the pioneer of quantum error-correction and quantum fault-tolerance, and it was a great opportunity and pleasure to discuss these matters with him. Here are some remarks in conclusion.
1) SLE as a model for decoherence of unitary evolutions.
The main purpose of my work is not to debunk quantum computers but to formally describe the interesting and important reality of quantum evolutions without quantum fault-tolerance, and thus to understand consequences of the failure of quantum computing/ quantum fault-tolerance. The main purpose of the smoothed Lindblad evolutions is to offer a model for realistic approximations to unitary evolutions which are subject to noise described by POVM-measurement. (Much of the discussion dealt with the issue of time scales and I will not attempt to summarize it here.)
2). Non-unitary evolutions.
Of course, in the context of quantum fault-tolerance we require also non-unitary evolutions to start with, and indeed the SLE conjecture should be extended to such evolutions as well. Large parts of the discussion above referred to such an extension which is yet to be carefully carried out. In particular, making sure that the conjectures are not violated by “restarts” of the quantum system is an important issue that Peter have raised.
3) Quantum fault-tolerance as a threshold phenomenon.
It is not a secret that I regard universal (or computationally-superior) quantum computation as implausible and at the end I expect that understanding quantum evolutions without quantum fault-tolerance will lead to understanding of why quantum fault-tolerance is not possible at all. But I regard the study of the barrier between quantum evolutions with quantum fault-tolerance and those without quantum fault-tolerance as important regardless of QC skepticism.
4) A correlation-based formulation:
One technical point. It can be handy to define “approximately smoothed noise” via a correlation property: The noise at time t,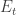
has significant correlation with 
5) Two analogies: solar-system transportation, and Kelvin’s “trivial flaw” in dating the earth.
Let me go again to the “trivial flaw” that I regard as crucial for the discussion: Current treatment of noise takes the universal quantum computation target for granted and ignore the possibility of systematic harmful relation between the noise and the evolution through the special device that implement the evolution. Let me be clear: current noise model do account for some relations between the noise and the evolution, but they account for that in a very limited way which is based on the general-purpose quantum device description. Klas gave a very nice description of my point of view while disagreeing with it!
I proposed the analogy with solar-system transportation. In order to build a general-purpose solar system transportation system, you need first to build special purpose transportation systems. For those risk-analysis can be substantially more complicated. If there are obstacles in principle for special purpose systems this may cause general-purpose systems to fail. A “threshold theorem” for general-purpose transportation systems can be completely blind to such a possibility.
The trivial flaw has some similarity to Kelvin’s “trivial flaw” in his dating of the earth (see this post and this one). Kelvin’s detailed analysis of heat-conductance missed the possibility that heat is transferred by hot material moving around. The detailed Hamiltonian models for noisy quantum evolutions (like those in Preskill’s paper), takes the universal QC for granted and miss the possibility that the noise systematically depends on the evolution through the specific device. These “trivial flaws” are important piece of the story but not the whole story, not in the case of dating the earth and not in our case of quantum computing.
6) An example: implementation of surface code using superconducting qubits.
There are several groups of researchers attempting to implement surface code using superconducting qubits. This is a very interesting project which is planned to be implemented over the next few years.
The physicists’ expectations are quite clear: for an implementation of distance five-surface codes that requires about a 100 qubits the encoded qubits will be much more stable compared to the physical superconducting qubits. Even with distance 3 codes which requires something like 25 physical qubits good quality encoded qubits are expected.
My predictions are also quite clear: The encoded qubits will not be more stable than the physical qubits. In fact, I expect the encoded qubits to be substantially less stable than the physical qubits and more so for the 5-distance case compared to the 3-distance case.
Let me say that I regard achieving encoded non-trivial qubits (via surface codes or other schemes) as a major scientific and technological breakthrough, but I predict that the stability of the encoded qubits will be significantly inferior to that of the physical qubits. Moreover I think that detailed modeling and (classical) computer simulation of the physical device may be used to test my predictions even before building the quantum device.
Let me also mention that the much acclaimed “Yale-group” achieved not long ago the first rudimentary quantum error correction in a solid state system! You can read about it here: At Yale, quantum computing is a (qu)bit closer to reality and the Nature article Realization of three-qubit quantum error correction with superconducting circuits, by M. D. Reed, L. DiCarlo, S. E. Nigg, L. Sun, L. Frunzio, S. M. Girvin, and R. J. Schoelkopf.
7) Teleportation
So now let’s take the plan for implementing surface code of distance 5 and make a larger plan where we double every qubit and we start the process of creating these surface with the 100 quibits owned by Alice and use teleportation to complete the creation of the surface code by the qubits owned by Bob, who rapidly departed Alice at high speed.
My claim is that the process for creating the 100-qubit surface code has a noise-component which is approximately SLE, and therefore the encoded qubit will not be stable, and that this continues to apply to the teleportation-process on the 200 qubits. Peter challenged my claim, based on an argument (that I don’t fully understand) that for the teleported system, nature will not know where precisely to “start” the SLE noise. (See here and several subsequent comments.) As far as I can see, the teleportation-based critique has the following problems: It ignores the approximation nature of the conjecture, it ignores the “trivial flaw,” and it ignores the fact that the conjecture, more than constraining the noise itself, excludes many unitary evolutions that can not be realistically approximated at all. (This last point is explained using an “identity card” example here.)
In any case, I think that if the SLE approximation and its conclusions are correct for the 100 qubits surface-code implementation, then teleportation will not save the day, not in theory and not in practice.
8) General points raised by Aram: In the debate and in some comments here Aram raised the following claims: The distinction between processes with and without quantum fault tolerance makes no more sense than the distinction between computer programs that involve QUICKSORT and those that do not; Pure states have no objective meaning; POVM-noise has no objective meaning; Noise, in general, have no objective meaning. Aram further claims that the formulation of my conjectures is heavily relying on the experimentalists’ intentions. These are interesting points (that we discussed also in the debate). Overall, I disagree with Aram regarding these points.
9) From what does SLE emerge? What is the fundamental law behind it?
This is also a point raised by Aram. My main difficulty with it is to understand what precisely is the question.
In any case, I do think that the failure to pass the quantum fault-tolerance barrier is related to several fundamental issues in physics. As I said in the lecture, in my opinion, the “trivial flaw” is an important part of the story but is not the whole story. (Michel Dyakonov’s stance can be understood as asserting that the “trivial flaw” is the whole story.)
Also here an analogy with Kelvin’s dating the earth can be drawn and also there Kelvin’s “trivial flaw” of regarding heat-conductance as the only mechanism for transferring heat is not the whole story. Before dating the earth, Kelvin was dating the sun. His estimates for the sun could not have taken into account nuclear reactions – not known at the time, and this mistake influenced his thinking regarding the earth.
Robert Alicki’s opinion that failure of quantum fault-tolerance is primarily related to thermodynamics (namely to the interface between quantum mechanics and thermodynamics) seems very reasonable to me. The quantum fault-tolerance barrier is related also to computations in quantum field theory (that motivated QC from the start,) and it can even be related to various issues in classical mechanics. At some point, Aram and I half jokingly considered to “smooth-in-time” expressions coming from QED, but we realized that both of us know too little about QED to even start 🙂 Interesting comments regarding quantum information and special relativity are here, where Aram answers questions I raised here.
Of course, my paper was not meant to be the last paper on the topic. Obviously, there are various things that I did not do, or that can be done better, and various relevant issues that I did not address.
Hi Gil,
Let me try to explain what Aram is trying to explain with point 8.
SLE noise has two critical properties. When you (conceptually) move it to the other side of a gate, then it is acted upon by the gate, so it effectively commutes with it. But when you (conceptually) move it to the other side of POVM noise, it doesn’t commute with that.
Now, suppose that you have some errors in your unitary gates, so you’re applying the wrong unitary transformations. It seems to me that nature shouldn’t be able to tell whether these were intentional variations in your gates, or whether they were a mistake that your controller made. So your SLE noise should commute with these errors, which you might call “noise from inaccurate unitary transformations”.
Now, let’s further suppose that the environment applies an extra small unitary transformation to your system. I don’t see how nature can distinguish between an unintended unitary transformation you made, and an unintended unitary transform that the environment made. Thus, the SLE noise should commute with the environment’s extra unitary transformation.
The problem is that there is no essential difference between an extra unitary transformation the environment makes (which extra unitary depends on the state of the environment) and the environment applying a POVM measurement to your state. This is because every quantum action has a back-action, so if the environment does something to your system, it is entirely equivalent to your system doing something to the environment. If your system does something to the environment, then the environment can be viewed as measuring the state of your system. So if you say that the SLE noise commutes with unitary operations, and does not commute with POVM measurements, this is a contradictory definition of SLE noise because any POVM measurements the environment makes on your system cannot be distinguished from unitary operations the environment applies to your system. If this distinction can actually be made, I believe that it would imply that quantum mechanics is non-linear.
Of course, if you look at SLE noise as not being anything “real”, but as an “identity card” that determines what kinds of unitary evolution/noise combinations are “valid”, this argument stops being a convincing argument against your SLE conjecture.
In fact, abstracting away all actual quantum physics, there will always be a “logical computational state space” that your system contains, and I don’t see any way to argue against the claim that SLE noise occurs in this logical computational state space. My teleportation example was intended to show that there is no possible physical source of SLE noise in computation by teleportation, but it seems to have completely failed to convince you.
Dear Peter,
“Of course, if you look at SLE noise as not being anything “real”, but as an “identity card” that determines what kinds of unitary evolution/noise combinations are “valid”, this argument stops being a convincing argument against your SLE conjecture.”
Yes, this is precisely how I think about it.
Of course, there are several examples in physics where the “identity card” picture turned into our mental “real” picture. (Also, less ambitiously, we can replace “valid,” by “without quantum fault-tolerance.” Aram QUICKSORT comparison notwithstanding.)
“My teleportation example was intended to show that there is no possible physical source of SLE noise in computation by teleportation”
I certainly want to come back to teleportation in this context and understand this issue better especially since Greg Kuperberg and I just wrote up a related old work. A basic difficulty I have with the teleportation argument is this: Suppose that you really try to implement that 100-qubit distance-5 surface code. My conjecture asserts that the actual evolution leading to the encoded state will have SLE noise component leading to non-stable encoded qubits. This can be true or false but so far teleportation has no role. Now suppose that you really try to extend the 100-qubits implementation and to implement the 200-qubits teleported version of the distance-5 surface code. What will the argument give? a) That the SLE conjecture (with the ID interpretation) must fail for the teleported system, but may still hold for the original 100-qubit version, b) That the SLE conjecture must fail for the 200 qubit version and, therefore, it must also fail for the 100 qubit version. c) something else.
The answer is (a): the SLE must fail for the teleported system.
I gave a talk at the HUJI CS theory seminar on matters related to my conjectures and the debate and there were several interesting comments by several participants, especially Dorit Aharonov, Michael Ben-Or, Nadav Katz , and Steve Wiesner.
1) Cat-state
Dorit suggested that experimental cat states with huge number of qubits are counterexamples for the conjecture on bounded depth computation.
This is a Good point!! I should certainly look at that.
2) Post-selection
My conjecture 1 is that the the quality of encoded qubits is essentially no better then the quality of physical qubits used for their construction. Dorit offered post-selection processes for purify qubits as a counter-argument. (I don’t think it works, though, I do not see why post-selection for encoded qubits is any better than post-selection for the physical qubits.)
3) Simulating physical experiments.
My overall opinion (expressed in the lecture) is that if quantum speed-up is not possible then, “in principle,” digital computers suffices to simulate the outcomes of robust (replicable) experiments in quantum physics. Here “In principle” refers only to the computational complexity of the best possible algorithm. Simulating natural quantum systems may depend on having the precise model, best algorithm for a solution, and, in particular, having the values of parameters that we do not have and perhaps will never have.
Dorit raised two related interesting points. The first was the (famous) question if processes without entanglement can be classically simulable. The second referred to the situation with 98% error rate. Those questions are interesting but, in my opinion, separate. For example, if there are processes without entanglement that are not classically simulable, then I suppose that nature cannot “run” them as well.
4) Slow down
Michael argued that my conjecture regarding smoothed Lindblad evolutions (with the additional conjecture on the rate of noise) fails as stated if you simply slow down the evolution by a large factor. He proposed to assume in addition that the identity operator is also subject to some noise (which he regards as a reasonable assumption.) The way I think that this issue should be handled is through the smoothing window. The engineering effort for quantum devices can is expressed by reducing the error-rate and reducing the smoothing-window. The smoothing window should also be scaled according to the same non-commutativity measure relevant for the rate of noise. A slow process implies that the smoothing window (in time units) is larger, and the error rate is smaller.
5) Single qubit evolutions (and refrigerators)
Nadav pointed out that single qubits can be robust as to allow millions of unitary operations. (Aram raised a similar point above.)
If indeed this is the situation then this is in tension with my conjectures (but not in a direct contradiction since my conjectures are about fault tolerance and about improving qubits quality by quantum error-correction.) Of course, there is no dispute that if we allow to re-initialize the qubit then we can have millions of operations and can go forever.
My conjectures are about approximately unitary evloutions that maintain the quantum information. (So if you refrigerate a single qubit you can go for ever but then you lose the information.) Steve actually referred to refrigerators as machines which carry over successfully something similar to what quantum fault-tolerance is about.
Hi Gil,
If they haven’t done so already, in a few years experimentalists will attempt to use quantum optical lattices to simulate the evolution of quantum systems with physical Hamiltonians that cannot currently be simulated on classical computers.
What is your prediction as to the results of these experiments?
Hi Peter, well it will be hard to make any prediction without knowing what specifically you refer too. (Also when you say: “..that cannot currently be simulated on classical computers” do you refer a) to our current understanding of the specific physics or b) to tasks we believe (but currently cannot prove) are computationally hard.)
So let me say a few things about quantum simulation. But before, your question reminded me a nice story about a guy who told his friends he plans to sell his new puppy. “How much do you ask, ” they asked, and his reply “one million dollars” left them a bit skeptical. After a few days they met him and asked if he got the million dollar. “Yes, sort of,” he replied, “I got for my puppy two kittens worth half a million each.”
Regarding quantum simulation. The idea to simulate using quantum optical lattices, quantum systems of other types is a beautiful idea. (To the best of my memory Hagai Eisenberg from HUJI have made some pioneering work on this topic in his Ph D.) Simulating a quantum system A using a quantum system B is certainly quite an important field, and the notion of “simulation” itself is probably much stronger then that of simulating with digital computers. I do not see any obstruction in principle for making such simulations. Of course, I would predict that both system A and system B satisfy my conjectures. E.g., that considered as approximated unitary evolutions they both have a substantial component of smoothed noise. In practice, perhaps some theoretical works on quantum simulation have some overly-optimistic ingredients taken from the theory of quantum fault-tolerance, but, this notwithstanding, I think that quantum simulation is a great field. (In analogy to the kittens story I would expect that neither system A nor system B demonstrate “quantum speed-up.”)
I am asking because you say
If you use an optical lattice to simulate another system, you know all the parameters (because you can tune them, and you can check that you’re tuning them correctly because if you tune them to a classically solvable system, you should get the right behavior).
Hi Peter, I am a little lost on what are we discussing here. Do you ask if optical lattice simulation of a quantum system X can make it easier to “figure out” the behavior of system X compared to classical simulations of the same system?
I am saying that you gave a list of possible reasons for why classical systems can’t simulate quantum systems. (“Simulating natural quantum systems may depend on having the precise model, best algorithm for a solution, and, in particular, having the values of parameters that we do not have and perhaps will never have.”)
If we can build quantum systems with tunable Hamiltonians, the first and last reasons are no longer relevant. The only excuse left for why we can’t simulate the system is that we don’t have the best algorithm.
Currently, there are lots of Hamiltonians that we can’t simulate well at all (e.g., the Hubbard model for many settings of the parameters). Right now, you can get away with claiming that we can’t simulate them because in nature, there is SLE noise that prevents them from behaving the way that our equations and small-number-of-qubit simulations predict they would. However, in a few years we should be able to create custom Hamiltonians using optical lattices, and show that these simulations really behave the way we think they should. We will then have real proof that nature does calculations that are hard for us to simulate.
One last comment: I actually think the success of lattice QCD computations (which take enormous amounts of computer time, and agree well with experiment) already shows that nature does computations we can’t simulate. But this is in the context of quantum field theory, not just quantum computation.
Peter,
1) “Currently, there are lots of Hamiltonians that we can’t simulate well at all (e.g., the Hubbard model for many settings of the parameters). Right now, you can get away with claiming that we can’t simulate them because in nature, there is SLE noise that prevents them from behaving the way that our equations and small-number-of-qubit simulations predict they would. However, in a few years we should be able to create custom Hamiltonians using optical lattices, and show that these simulations really behave the way we think they should. We will then have real proof that nature does calculations that are hard for us to simulate.”
Yes, I agree with that.
In fact, you just made the predictions for me 🙂 .
(Indeed, there is something a little counter-intuitive in what I am suggesting: the simple Hubbard model for a certain range of parameters may be computationally intractable, and yet the much more complicated (and yet unknown) model for how related systems from solid state physics really behave is computationally feasible. But this may well be correct. BTW if you can link me to what you refer to regarding optical lattices, I will be thankful.)
2) ” I actually think the success of lattice QCD computations (which take enormous amounts of computer time, and agree well with experiment) already shows that nature does computations we can’t simulate. But this is in the context of quantum field theory, not just quantum computation.”
Yes, huge massive QCD computations (or QED computations) that agree well with experiment indeed tend to support the idea that nature does computations that we can’t simulate. But this is an indirect support that may fail on close scrutiny.
3) The flip side is this: How exactly are you going to to create custom Hamiltonians using optical lattices without full-fledged quantum fault-tolerance and quantum error-correction? If QED/QCD computations are computationally intractable, can nature “run” them without a mechanism of quantum fault-tolerance? If not, how? If yes, how?
Here is one article about optical lattices and simulation. There are lots more of them.
For your point (3), I think the idea is that both real condensed matter systems and optical lattices are going to have slightly imperfect Hamiltonians, but that the simulation will still work because the behavior of the Hubbard model with a small amount of decoherence is relatively robust (unlike quantum computations).
We had here in Jerusalem a great quantum information conference, QSTART to which I will be happy to devote a whole post. Also on the matter of my quantum computers skepticism, I heard many interesting comments, and let me write about them here while they are more or less fresh in my memory. Perhaps sometime later I will develop these comments to a separate post. Streaming video of the talks is now available.
In part in response to Umesh Vazirani who asked me for a quick description of the crux of matters in my point of view, I gave a five minute lecture in the rump session on my stuff, and I started with a short welcome as an organizer. Being the oldest organizer it was only appropriate that my introduction was on quantum information in Jerusalem B. C.
So here are a few comments from a few people:
1) Comments by Daniel Gottesman. Daniel is both a pioneer and a leader in quantum fault-tolerance, and he had various interesting comments on my stuff.
Clifford gates – A famous theorem of Gottesman-Knill asserts that quantum computation with only Clifford gate can be simulated classically. On the other hand, having a quantum computer that emulate quantum evolutions with only Clifford gates seems to require (at least partial) quantum fault-tolerance, so I would expect that devices capable to create such quantum evolutions are already in conflict with my conjectures (e.g. SLE noise will not allow them). This is the place where the quantum fault-tolerance barrier can be different from the quantum speed-up (or quantum-supremacy) barrier. There are several other interesting issues related to QC with noiseless Clifford gates, and fault tolerance.
Reversible quantum computation. – Daniel mentioned reversible quantum computation. For certain depolarizing noise restricting to the reversible case leave you with log-depth quantum computation. But for other types of noise, polynomial-time or even exponential time computation is possible!! This is a recent result of Ben-Or, Gottesman, and Hassidim. Moreover, in this case it is the best-possible noise when you mix various types of noise determine the outcome! Actually, I knew about some early versions of the result, and it started from a discussion Michael, Dorit and I had in summer 2005 with Robert Alicki. Very impressive result!
Square root fluctuations. One of my concerns with Hamiltonian noise-models is that I suspect the fluctuations of the number of errors to be proportional to square root the number of qubits (or particles,) which I suspect is unrealistic for interacting systems. Without agreeing with me that square-root fluctuation is unrealistic, Daniel thinks that this will not be the case for a model used in the paper by him and Aliferis where the possibility of fault tolerance is governed by a certain norm. (I did not find the specific paper so I will ask Daniel about it. This is worth checking. I wonder how this norm can capture the distinction between error rate in a bounded interval, below the threshold, where quantum fault-tolerance is possible, and error rate which is itself Gaussian with mean well below the threshold and very small variance, where fault tolerance is impossible.)
The trivial flaw – Overall, Daniel did not agree with what I refer to as the “trivial flaw,” but I think I did manage to make my point on this matter clearer. (The solar-transportation system is a useful analogy.)
What about Theorems – Daniel expressed the view that it will be nice if I could present some theorems and not just conjectures. E.g., a theorem of the form “SLE noise does not enable quantum fault-tolerance.” Since proving theorems is my main business I could not agree more, although here, I saw it as important to think about modeling. Also proving theorems is difficult. Actually, it will be nice to prove that reversible quantum computation with SLE noise does not allow quantum fault-tolerance. Maybe (but I am not sure about it) this will allow to ignore the need to discuss non-unitary intended evolutions.
2) Comments by Umesh Vazirani.
Testing QM – There is a paper by Umesh with Dorit about interactive quantum proofs as a sort of a new paradigm in philosophy of science. Usually when I think about the argument I disagree, but when I hear about it from charismatic Dorit (and this time from Umesh) I am somehow short-termed convinced.
QM breakdown – It looks that Umesh thinks that it is a serious possibility (or at least that this should be considered as a serious scientific possibility) that QM will break-down for complex systems (say, with hundreds of qubits). Somehow, I think that it is a more serious possibility that the assumptions on decoherence for results on quantum fault-tolerance are unrealistic in an non-repairable way.
3) A comment by Nadav Katz
Experimental quantum error-correction. Nadav asked (again) if the recent experimental work on quantum error-correction where several groups managed to improve the quality of logical qubits (for genuine noise) compared to the quality of the physical qubits do not violate my conjectures.
The answer is that indeed the successful experimental work on quantum error-correction goes against my conjectures. I don’t think that the actual “scalability” or “quantum fault-tolerance” barrier had been crossed but the progress is steady, researchers, while being aware of all sort of obstacles, are overall optimistic, and don’t see major obstacles that cannot be overcome. There are very concrete ideas and plans for experimental work that by my own view will cross the barrier and will convince me that I am wrong. But this did not happen yet. This is a schematic picture of experimental progress approaching the fault-tolerance barrier, and plans of crossing it.
Implementing Surface codes. There were several very interesting talks about experimental quantum information. John Martinis talked about prospects for having, based on surface codes implemented with superconducting qubits, high quality maneuverable logical qubits based on lower quality physical qubits. Let me be clear about it – if surface codes can indeed be realized and meet expectations regarding the quality of encoded qubits, this will smash my conjectures to pieces. I already expressed enthusiasm about this approach after hearing David DiVincenzo talking in our seminar, and it was very interesting to here about the experimental aspects. (There are two groups of researchers attempting separately to implement surface codes based on superconducting qubits.)
4) A comment by Ray Laflamme.
Ray Laflamme who was one of the pioneers of the threshold theorem and admirably moved from theoretical physics to become an experimentalist in order to test if quantum fault-tolerance is possible, gave a great opening talk about experimental error-correction. Later, he told me that my short lecture invoked him to wonder how my suggestions could be checked experimentally. Of course, I was happy with this remark.
5) People’s motivations for entering QI
Edi Farhi told how Shor’s algorithm was the reason for him to move to QI from particle physics. (I think This was the trigger also for John Preskill. John did no come this time but will co-direct with Michael Ben-Or, and Patrick Hayden, a winter school here in Jerusalem on physics aspect of quantum computations – stay tuned.)
Both Michael Ben-Or and Ray Laflamme wanted initially to show that quantum computers are not possible by proving that quantum fault-tolerance is impossible for arbitrary small constant error-rate. (I mentioned it in my lecture and jokingly remarked that they were not persistent enough.) Usually, I don’t ask people about their beliefs regarding QC, but I made an exception and asked over dinner Michael (the first time in 8 years) what is his view today, and he said that he now believes that QC can be built!
I plan to give the second slide of my welcome presentation and say few things about my 5-minutes presentation in a separate comment.
Here is my five-minutes rump talk at QSTART. It consisted of five pictures with brief verbal explanations (that I try to reproduce here) and two other slides (that I simply read out).
My expectation is that the ultimate triumph of quantum information theory will be in explaining why quantum computers cannot be built, and my research is geared in this direction. Incidentally, this was the initial motivation of Michael Ben-Or and Ray Laflamme in studying quantum fault-tolerance. But Michael and Ray were not persistent enough 🙂
To this end – drawing formally the barrier between quantum processes with quantum fault-tolerance and those without is important. This barrier represents an interesting phase transition even if quantum computers are possible.
When you restrict yourself to general-purpose quantum devices, the possibility for quantum fault-tolerance reduces essentially to a single parameter. Modeling general-purpose devices is much too narrow to deal with the issue of scalability. Ignoring it is responsible for wrong arguments and intuitions for why quantum computers must be possible.
Universal classical computing devices are still special-purpose quantum devices. (Forgetting it accounts for further wrong intuitions and arguments.)
Smoothed Lindblad evolutions is a mathematical tool aimed to draw formally the quantum fault-tolerance barrier.
Smoothed Lindblad evolutions form a subclass of general Lindblad evolutions, and thus they are entirely withing the framework of QM.
Physicist Michel Dyakonov opines that quantum computer will fail and this will have no baring on our understanding of physics. Scott Aaronson compares a supposed understanding for why QC cannot be built to a scientific revolution of magnitude seen only once or twice in human history. Looking at this picture of the quantum landscape, I regard a definite understanding for why quantum computers must fail as a mild earthquake which will still have wide applications to the interface between quantum mechanics and other layers of physical laws. (In the picture, the QC project is demonstrated by an artist view for the biblical tower of Babylon :). )
And here is the second slide of my “Quantum Information B. C.” welcome.
Of course, B. C. stood for: “before center” and I briefly told about a few quantum information and computation people in Jerusalem before the center was formed, and before experimentalists working on quantum information, Hagai Eisenberg and Nadav Katz, joined HUJI and enabled us having a well balanced interdisciplinary center. Starting with Michael Ben-Or, who was the first HUJI computer scientists to get interested in quantum information in the late 80s*, and moving clockwise, we see Ofer Biham, now the head of Racah Institute of physics at HUJI, Avi Wigderson, a theoretical computer scientist and a mathematician now at IAS, Daniel Lidar a Ph. D student of Ofer (and Benny Gerber) now at USC, Ilan Kremer, who did M. Sc with Noam Nisan on quantum computation, moved to economics and finance and now is the director of the Center for the Study of Rationality at HUJI, Ronnie Kosloff, a theoretical chemist, Dorit Aharonov, who before “the rest is history” phase, did her M. Sc, and Ph. D. on quantum computation with Noam , Michael, and Avi, and Itamar Pitowski, a philosopher of science who passed away a few years ago. Itamar studied the foundations of quantum physics, and of probability theory and was among the first to formulate the “efficient Church-Turing thesis.” Last but not least is Noam Nisan, a theoretical computer scientist, game theorist and economist here at HUJI. (*) Maybe Noam Nisan got interested in QC around the same time in Berkeley.
Pingback: Aaronson and Arkhipov’s Result on Hierarchy Collapse | Combinatorics and more
Pingback: Pictures from Recent Quantum Months | Combinatorics and more
There’s a small problem with your algorithm Dr. Shor.
I refer specifically to a certain non-trivial unitary matrix that got implicitly inverted with O(1) time complexity.
But since I am just a poor time-travelling anthropologist, I probably have no right to speak…
It’s an easy mistake to make. Because transposing a matrix “feels” O (1). You’re just reflecting it in a mirror after all.
If, however your matrix represents a physical quantum circuit, then you are actually going to have to “unplug” and “replug” n gates. Which is definitely O (n).
Unless there is some magic “quantum mirror” which nobody has told me about, which can redo the “wiring” in some other way. Like a natural isomorphism his between V and V^*. Is there an inner product I don’t know about?
A physical inner product.