Feng Pan and Pan Zhang uploaded a new paper on the arXive “Simulating the Sycamore supremacy circuits.” with an amazing announcement.
Abstract: We propose a general tensor network method for simulating quantum circuits. The method is massively more efficient in computing a large number of correlated bitstring amplitudes and probabilities than existing methods. As an application, we study the sampling problem of Google’s Sycamore circuits, which are believed to be beyond the reach of classical supercomputers and have been used to demonstrate quantum supremacy. Using our method, employing a small computational cluster containing 60 graphical processing units (GPUs), we have generated one million correlated bitstrings with some entries fixed, from the Sycamore circuit with 53 qubits and 20 cycles, with linear cross-entropy benchmark (XEB) fidelity equals 0.739, which is much higher than those in Google’s quantum supremacy experiments.
Congratulations to Feng Pan and Pan Zhang for this remarkable breakthrough!
Of course, we can expect that in the weeks and months to come, the community will learn, carefully check, and digest this surprising result and will ponder about its meaning and interpretation. Stay tuned!
Here is a technical matter I am puzzled about: the paper claims the ability to compute precisely the amplitudes for a large number of bitstrings. (Apparently computing the amplitudes is even more difficult computational task than sampling.) But then, it is not clear to me where the upper bound of 0.739 comes from? If you have the precise amplitudes it seems that you can sample with close to perfect fidelity. (And, if you wish, you can get a F_XEB score larger than 1.)
Update: This is explained just before the discussion part of the paper. The crucial thing is that the probabilities for the 2^21 strings are distributed close to Porter-Thomas (exponentials). If you take samples for them indeed you can get samples with F_XEB between -1 and 15. Picking the highest 10^6 strings from 2^21 get you 0.739 (so this value has no special meaning.) Probably by using Metropolis sampling you can get (smaller, unless you enlarge 2^21 to 2^25, say) samples with F_XEB close to 1 and size-biased distribution (the distribution of probabilities of sampled strings) that fits the theoretical size biased distribution. And you can also use metropolis sampling to get a sample of size 10^6 with the correct distribution of probabilities for somewhat smaller fidelity.
The paper mentions several earlier papers in this direction, including an earlier result by Johnnie Gray and Stefanos Kourtis in the paper Hyper-optimized tensor network contraction and another earlier result in the paper Classical Simulation of Quantum Supremacy Circuits by a group of researchers Cupjin Huang, Fang Zhang, Michael Newman, Junjie Cai, Xun Gao, Zhengxiong Tian, Junyin Wu, Haihong Xu, Huanjun Yu, Bo Yuan, Mario Szegedy, Yaoyun Shi, and Jianxin Chen, from Alibaba co. Congratulations to them as well.
I am thankful to colleagues who told me about this paper.
Some links:
Scientists Say They Used Classical Approach to outperform Google’s Sycamore QC (“The Quantum” Written by Matt Swayne with interesting quotes from the paper. )
Another axe swung at the Sycamore (Shtetl-Optimized; with interesting preliminary thoughts by Scott; )
Update (May, 25, 2021): Scott referred again to Pan and Zhang’s paper in a recent post largely repeating his preliminary thoughts on the matter.
Q: What do you generally think about improvements in tensor network methods as a challenge to quantum supremacy and the recent simulation of the supremacy result in Beijing?
SCOTT: I blogged about this here. It was a clever paper, which showed that if you focus narrowly on spoofing the linear cross-entropy benchmark used by Google, then there’s a classical algorithm to do that much faster than had been previously pointed out, by generating many samples that all share most of their bits in common (e.g., that all agree on the first 30 of the 53 bits). But many people remain unaware that, if you just changed the benchmark – for example, if you insisted that the returned samples not only pass the linear cross-entropy benchmark, but also be sufficiently different – then this classical spoofing strategy wouldn’t work and we’d be back to the previous status quo.
- You cannot change the benchmark to make the Google experiment pass the benchmark and the spoofing experiment fails the experiment in an arbitrary way. Your benchmark needs to be based on some theory. Passing the linear cross-entropy benchmark has some theoretical justification. Those justifications leave open the question of the computational hardness kick in for 53 qubits. The spoofing suggests that 53 qubits simply do not suffice for the asymptotic computational complexity insights to apply and certainly not to support the far-reaching claims in the Google paper.
- You need a precise benchmark. Scott’s requirement that the returned samples are also sufficiently different is vaguely stated.
- If you mix the sample produced in the new paper with a uniform sample (as mentioned in the Pan and Zhang’s paper) it is likely that you will not be able to statistically distinguish between samples based on Google model and spoofed samples.
- On top of that, from the statistical study of the Google samples by Rinott, Shoham and myself, we now know that the Google samples will be considerably “less different” then samples based on the Google model.
(Regarding the third point, Pan and Zhang referred to it in footnote [26]: “Notice that the correlation issue of our method can be significantly relaxed by selecting some large-probability bitstrings, then mixing them with a large number of random samples. For example, if we select 220 bitstrings with top probabilities and mix with 999780 random bitstrings, the correlations among the overall 1 million bitstrings would be negligible, while the would be 0.002, the same as Google’s experiments”)
Update: in the comment section I mentioned various further remarkable advancements by several groups of researchers. Most recently Liu et al. managed to compute the actual amplitudes of one circuits of the Google 53 qubits depth 20 circuits in the paper Validating quantum-supremacy experiments with exact and fast tensor network contraction.


Update: Some more discussion based on a recent SO post is added.
Update: In a very recent paper Feng Pan, Keyang Chen, and Pan Zhang have solved the uncorrelated sampling problem of the Sycamore quantum supremacy circuits. They efficiently generate independent bitstrings and claims that the running time is roughly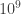 faster compared to Google’s claims. (So on the supercomputer for which the Google paper estimated that 10,000 years of computations are needed the new algorithm would require a few dozens seconds.) See, https://arxiv.org/abs/2111.03011.
faster compared to Google’s claims. (So on the supercomputer for which the Google paper estimated that 10,000 years of computations are needed the new algorithm would require a few dozens seconds.) See, https://arxiv.org/abs/2111.03011.
Here are three other recent important papers on classical simulations of quantum circuits
1) Recursive Multi-Tensor Contraction for XEB Verification of Quantum Circuits
by Gleb Kalachev, Pavel Panteleev, Man-Hong Yung
https://arxiv.org/abs/2108.05665
2) Closing the “Quantum Supremacy” Gap: Achieving Real-Time Simulation of a Random Quantum Circuit Using a New Sunway Supercomputer by Yong (Alexander)Liu, Xin (Lucy)Liu, Fang (Nancy)Li, Haohuan Fu, Yuling Yang, Jiawei Song, Pengpeng Zhao, Zhen Wang, Dajia Peng, Huarong Chen, Chu Guo, Heliang Huang, Wenzhao Wu, Dexun Chen–
https://arxiv.org/abs/2110.14502
3) Redefining the Quantum Supremacy Baseline With a New Generation Sunway Supercomputer, by Xin Liu, Chu Guo, Yong Liu, Yuling Yang, Jiawei Song, Jie Gao, Zhen Wang, Wenzhao Wu, Dajia Peng, Pengpeng Zhao, Fang Li, He-Liang Huang, Haohuan Fu, Dexun Chen
https://arxiv.org/abs/2111.01066
Another paper: Spoofing Linear Cross-Entropy Benchmarking in Shallow Quantum Circuits, by Boaz Barak, Chi-Ning Chou, Xun Gao. https://arxiv.org/abs/2005.02421
(See it also among other QC breakthroughs in this SO post https://scottaaronson.blog/?p=4794 )
And: Limitations of Linear Cross-Entropy as a Measure for Quantum Advantage by Xun Gao, Marcin Kalinowski, Chi-Ning Chou, Mikhail D. Lukin, Boaz Barak, and Soonwon Choi
Pingback: Good Codes papers are on the arXiv | Combinatorics and more
Pingback: “Waging War on Quantum” | Combinatorics and more
Pingback: Ordinary computers can beat Google’s quantum computer after all | Combinatorics and more
Major further progress is reported in the paper: Validating quantum-supremacy experiments with exact and fast tensor network contraction, by Yong Liu, Yaojian Chen, Chu Guo, Jiawei Song, Xinmin Shi, Lin Gan, Wenzhao Wu, Wei Wu, Haohuan Fu, Xin Liu, Dexun Chen, Guangwen Yang, and Jiangang Gao.
The link is https://arxiv.org/abs/2212.04749
Liu et al. were able to compute the amplitudes for Google’s ultimate samples in the 2019 supremacy experiment. (This is considerably harder than producing sample of the same quality as Google’s.) Their computation confirms Google’s fidelity estimates.
Pingback: Greatest Hits 2015-2022, Part II | Combinatorics and more
Pingback: Questions and Concerns About Google’s Quantum Supremacy Claim | Combinatorics and more
Pingback: My Notices AMS Paper on Quantum Computers – Eight Years Later, a Lecture by Dorit Aharonov, and a Toast to Michael Ben-Or | Combinatorics and more