Test your intuition:
You throw a dice until you get 6. What is the expected number of throws (including the throw giving 6) conditioned on the event that all throws gave even numbers.
Recent Comments
TYI 30: Expected number of Dice throws
This entry was posted in Combinatorics, Probability, Test your intuition and tagged Elchanan Mossel, Test your intuition. Bookmark the permalink.
Combinatorics and more 
I would have thought bigger than two. I calculate three.
This seems so obvious — completely different from the usual “test your intuition” questions (like the previous one). What am I missing?
Who can say?! The answer seemed obvious to me for a few seconds, and then it stopped seeming obvious. Then a different answer became obvious, but only after some thinking 🙂
I had the same thing. I read the question, answered the poll with the first obvious answer (thinking first is cheating), thought for a few more seconds, and I am now sure that the second obvious answer is true.
Then I tried to make bad student’s mistakes and they were also options in the poll (one of them has place third in the current poll), so I think that there are at least three obvious answers.
As long as at each given moment there are no two contradictory obvious answers there is no global threat for mathematics as a whole.
Lior, I realize that it is important to have obvious questions from time to time so that readers’ intuition will not be tilted to the non-obvious.
Exactly!
A surprisingly nice question! What is the etiquette – can we spoil with comments down here, or should we wait a while…
Dear James, please comment on the new post coming soon.
Dear Lior and James, It is certainly easier than TYI 29. I shall reveal what people’s intuition was, and propose to wait for a detailed solution to the solution post.
Outcomes after 180 votes
Lovely results! I would love to know what kind of intuition leads someone to guess 1 here.
At least the truth comes in second.
By the way, the question was invented by Elchanan Mossel during a undergrad class. Students asked Elchanan to give more examples and he invented it on the spot (it was at Penn in 2014-15).
Actually while I gained your attention, I wonder if you regard the following exchange in a lecture funny or not:
Speaker: Aldous answered a conjecture of Mezard and Parisi and showed that in the limit the expectation for the assignment problem is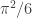
.
Question from the audience: Did it confirmed or refuted the conjecture?
Another voice from the audience: Mezard and Parisi conjectured that the answer is not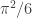
and Aldous refuted this conjecture!
Dear Gil,
A quibble. When I first read the question I was unsure if you meant a single FAIR die or a pair of FAIR dice were thrown. On rereading I decided you meant a single fair die.
Dear Joe, should I correct the English?
From the discussion I think everyone understood.
Yes, it is a single die rather than dice.
I thought dice is kosher for single as well.,,
Sorry, no dice 😉
What I saw was that: If you look up dice in the Oxford Dictionary, you will learn that dice is an acceptable singular and plural form of die. According to this source, dice was once the plural of die, “but in modern standard English dice is both the singular and the plural: ‘throw the dice’ could mean a reference to either one or more than one dice.”
Since I told Gil the story today, I will share the nicest explanation, that I heard from Paul Cuff.
Rephrase the question as follows: Toss a die until the first time T that the result is different from
2 and 4. What is the mean of T?
Finally, observe that T is independent of the value among 1,3,5,6 obtained in the T’th toss, so conditioning that value to be 6 does not affect the mean of T.
Pingback: Elchanan Mossel’s Amazing Dice Paradox (answers to TYI 30) | Combinatorics and more
Fantastic!
I can’t wait to unleash this on my students.
So what is the correct answer ?:)
I calculated 3….
That is a very elegant solution indeed. Here is a very different one – less compact, but with an ingredient that may be of general interest.
Consider a bet B on the number of throws: you get T dollars when the T-th throw is 6 after only 2s and 4s; as soon as a throw gives an odd number, the bet stops. Upfront you pay the mean payoff, call it x, but you get it back in the latter case. Then x is the answer to the puzzle.
It can be determined as follows. The payoff is
“1 if 6, x if 1,3,or 5, B’ if 2 or 4” (*)
Here B’ is the induced bet as of the second throw, “2 if 6, x if 1,3,or 5, B’’ if 2 or 4”, with B’’ the bet as of the third throw, etc.
Bet B’ has the same mean payoff as B+1/4: B’ pays 3/4 more when the last throw is 6 (probability 1/3), 1/4 less when it is odd (probability 3/4). So x must be the mean payoff of
“1 if 6, x if 1,3,or 5, x+1/4 if 2 or 4”,
and the solution follows.
Note: to replace B’ by x+1/4 is specific to the puzzle, but the idea behind using x in the payoff (*) relies on a very general idea: fixed point updating. It covers Bayesian updating as a special case, without reference to probabilities. The interested reader is referred to a post (August 18) on this topic at the Decision Theory forum at groups.google.com.
– Berend Roorda, University of Twente
I used to think “the die is cast” meant something like “the mold is set” — see Wikipedia’s “Die (manufacturing)” — rather than “the dice [sic] is thrown”. 🙂
This is a funny question. You have to define ‘expected’ and for a single die.
Then the number N for the number of throws will be in the range 1 < N < infinity (with very bad luck) and the probability curve peaking at pi!
Previous 2 and 4 throws don't count.
Pingback: Exploring Elchanan Moddel’s fantastic probability problem with kids | Mike's Math Page
Pingback: Exploring Elchanan Mossel’s fantastic probability problem with kids | Mike's Math Page
I got it wrong. Looking at the solution (where you ask about the first time you don’t get a 2 or a 4) I had a very nice ah ha/oohhhh experience. When I tried to go through it by figuring out the probability of getting an all even sequence I noticed something interesting. It’s 1/4, which means conditioned on getting only even numbers until a 6 the probability of getting a 6 on the first role is (1/6)/(1/4)=2/3. After the fact I can see why, if you get a 6 on the first roll then the game ends and you’re in the “all even” subworld, if you get a 2 or 4 you might (3/4 of the time) not be in the “all even” sequence world.
For intuition, does this remind anyone else of the Monty Hall problem? (Where realizing that conditioning really amounts to only caring about the average length of a die-generated sequence of 2’s and 4’s is sort of like realizing conditioning really amounts to only caring about whether the prize is behind the door that you originally picked.)
Really good problem! I makde a script to let everyone experiment and see why the correct answer is correct: http://www.airapport.com/2017/09/a-very-interesting-math-problem-with.html
It’s interesting that the answer doesn’t change, if you change the rule to stop on the first 5 or 6.
Pingback: A Probability Puzzle That You’ll Get Wrong | Math with Bad Drawings
Pingback: Counterintuitive Dice Probability: How many rolls expected to get a 6, given only even outcomes? | Dispatches from the Untrammeled Mind
Yuval’s elegant solution makes a creative leap to the problem of
throwing until a value other than two or four comes up, but I prefer a
simple approach that sticks to the original formulation of throwing a
six-sided fair die until the first six comes up.
Namely, the probability of the six-sided fair die throwing all evens
is unchanged if the first throw is two. That is, the probability of
throwing all evens is independent of the first throw being two. But
independence implies that conversely the probability of first throwing
two given all evens is the same as the probability of first throwing
two, namely 1/6; same for the probability of first throwing four given
all evens. It follows that the remaining possibility of first
throwing six given all evens has probability 1 – 1/6 – 1/6 = 2/3.
This reasoning applies equally well to the next throw after any
sequence of twos and fours given all evens, so throwing until a six
appears on the fair six-sided die, given that all throws are even,
is the same as throwing until a six appears on a three-sided die whose
probabilities of rolling two, four, and six are respectively 1/6, 1/6,
and 2/3. Of course the expected time for this unfair three-sided die
to roll a six is 1/(2/3) = 3/2.
Incorrect sketch ,if you hold the dice, focus on one side and count the spots, then look at the opposite side- count the spots and the total number of spots on those two sides should add up to 7
This is not a dice! The opposite faces must add to seven.
Pingback: Personal Learning and Development – Students into Education
Pingback: Talking conditional expectation with the boys thanks to examples from Alex Kontorovich and Gil Kalai – Mike's Math Page
Pingback: Understanding The Math Behind Elchanan Mossel’s Dice Paradox ~ Mathematics ~ mathubs.com
Pingback: Experimental Mathematics - Justin's Blog
Pingback: Greatest Hits 2015-2022, Part I | Combinatorics and more
Pingback: Throwing Dice Problem – Math, Physics, Misc ,Blog
That is not a true dice – three and four belong
on opposite sides of the dice.
Pingback: ChatGPT Meets Elchanan Mossel’s Dice Problem | Combinatorics and more