The Quantum Computer Puzzle
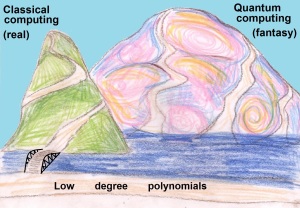
My paper “the quantum computer puzzle” has just appeared in the May 2016 issue of Notices of the AMS. Here are the beautiful drawings for the paper (representing the “optimistic view” and the “pessimistic view”) by my daughter Neta.
And the summary of my view
Understanding quantum computers in the presence of noise requires consideration of behavior at different scales. In the small scale, standard models of noise from the mid-90s are suitable, and quantum evolutions and states described by them manifest a very low-level computational power. This small-scale behavior has far-reaching consequences for the behavior of noisy quantum systems at larger scales. On the one hand, it does not allow reaching the starting points for quantum fault tolerance and quantum supremacy, making them both impossible at all scales. On the other hand, it leads to novel implicit ways for modeling noise at larger scales and to various predictions on the behavior of noisy quantum systems.
The nice thing is that my point of view is expected to be tested in various experimental efforts to demonstrate quantum computational supremacy in the next few years.
Updates (April, 24 2016): Here is an expanded version of the paper, with references, additional predictions and discussion. Here is a related post on GLL.
Polymath10 Plans, polymath11 news, and other plans.
The plan for polymath10: I hope to come back to it soon, report on some computer experimentation and, of course, further comments on post 4 are most welcome. I hope to be able to report on some computer experimentation regarding the various conjectures and ideas. I am planning to launch a fifth post in May. Overall, I consider one year as a good time span for the project. Post 4 of Polymath11 is still active on Gowers’s blog, and I think that a fifth post is also in planning.
Here on the blog, I plan a mathematical post about my visit to Yale on February. The visit have led to Stefan Steinerberger’s beautiful post on Ulam sequences. There are also newer interesting things, from our combinatorics seminar at HUJI, and from the third Simons’ conference on the analysis of Boolean functions (I hoped Ryan will blog about the conference). In celebration of the recent breakthrough on sphere packing in dimensions 8 and 24 I also plan to write more on sphere packing.
Happy Passover!
Pictures with Avi Wigderson at Nogafest and with Alex Lubotzky at Yale.




The original positivist interpretation of quantum mechanics forces QC people to admit that certain non-empirically verified assumptions hold, such as unitary, psi-ontic wave functions, linearity, etc.. Just about every field of science attempts to quantify counterfactuals and probability in QM is no more needed than in any other branch of science. Everything in QM follows from the uncertainty principle and that only gives support to the idea that we use probabilities to describe OUR uncertainty! The system could even be chaotic. To get probabilities, you are assuming classical particles but there are no classical particles. Quantum mechanics really predicts the expected values of observables and it does not measure probabilities.
The so-called “negative probabilities” are in a quasiprobability distribution where the anomaly is created at less than hbar and there are no final negative probabilities. By the way, the wave function of an electron is a complex-coefficient spinor function, which isn’t just a simple amplitude. The wave function can be positive, negative, complex, spinor or vector. Note that mathematicians have found quantum probability to be useless for modeling anything but atomic particles.
Just because simulating quantum states requires a high Turing complexity does not mean the argument runs backwards because the exponential computation on the wave function may well have nothing to do with the physical system of something like an dumb electron. I believe many in the QC community subscribe to the Schrödinger’s cat fallacy. The fallacies here are as persistent as those about EPR non-locality. QCs may not be possible at all given that they go beyond the current accepted theory of QM. People need to be honest about that. People making money building them are not honest, however.
Roger Schlafly writes:
“Quantum mechanics is a system for tracking the potential observations of atoms, and other phenomena on that scale. In particular it allows calculating probabilities of multiple possibilities, even though single outcomes are observed.
A quantum computer is a conjectural machine to do computations from interpreting those multiple possibilities as separate realities that can each contribute to what appears to be an almost-magic parallel computation. Despite almost a billion dollars in investment, no such speedups have been achieved.”
I have read your Notices paper with great interest, but have a question which is far from main theme of the paper. You mention on p. 510 “average of all unit vectors in the associated Hilbert space”. I am very far from quantum mechanics, but would guess that in reality the number of pure states that a system can be in is infinite, hence the “associated Hilbert space” is infinite-dimensional, isn’t it? If so, how can you define “average of all unit vectors” in the infinite-dimensional space, given that there is no convenient analogue of Lebesgue measure in infinite dimension?
Dear Bogdan, the description of the depolarizing noise is for a qubit where the Hilbert space is two-dimensional.
Pingback: The US Elections and Nate Silver: Informtion Aggregation, Noise Sensitivity, HEX, and Quantum Elections. | Combinatorics and more
Pingback: Why Quantum Computers Cannot Work: The Movie! | Combinatorics and more
Pingback: The Race to Quantum Technologies and Quantum Computers (Useful Links) | Combinatorics and more
Pingback: Some Mathematical Puzzles that I encountered during my career | Combinatorics and more
Pingback: If Quantum Computers are not Possible Why are Classical Computers Possible? | Combinatorics and more
Pingback: Greatest Hits 2015-2022, Part I | Combinatorics and more
Pingback: My Notices AMS Paper on Quantum Computers – Eight Years Later, a Lecture by Dorit Aharonov, and a Toast to Michael Ben-Or | Combinatorics and more