TYI 30 asked Elchanan Mossel’s Amazing Dice Paradox (that I heard from Yuval Peres yesterday)
You throw a die until you get 6. What is the expected number of throws (including the throw giving 6) conditioned on the event that all throws gave even numbers?
Most people answered 3.
Is it the right answer?
No!
Please use now the comments thread to offer your answers, explanations, insights, intuition, thoughts and after-thoughts. I am especially eager to hear your take, James Martin! For a nice explanation by Paul Cuffis, see this comment by Yuval.
Comments on the English dilemma between “a die” or “a dice” are also welcome.
(Let me also draw your attention to TYI 29 about exciting models of random trees.)
Combinatorics and more 
Pingback: TYI 30: Expected number of Dice throws | Combinatorics and more
I just assumed it would be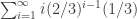
. Obviously more to it”
Ah! The last probability is 1/6!
Very interesting I have a hard time finding a flaw in the simple calculation –
1) From bayes formula P(6|even)=1/3.
2) The number of throws needed follows a Geometric distribution with $p=1/3$, and therefore the mean is 1/p=3.
The conditioning is more subtle. It is NOT that all throws are even, but that all throws until the first 6 are even.
I realize that I didn’t give enough context in my comment.
I’m referring to a modified version of the experiment in which the thrower continues to throw the die even after the first 6 occurs.
Ok now it makes perfect, I mis-understood the question. Thanks!
An intuition for whats wrong with the naive thinking.
Suppose you throw a die with with 1,000 sides instead of 6, until you get a 6 conditioned that all throws gave 2, 4 or 6 (let’s refer to this as a “valid sequence”). According to the naive thought, the answer should still be 3.
Recall that the probabilities in the conditioned probability space are proportional to the probabilities in the original space.
In the original space, the probability for a valid sequence of length 1 is 1/1,000, and the probability for a valid sequence of length at least 2 is at most 6/1,000,000 (because the first throw needs to be 2 or 4, and the second throw needs to be 2, 4 or 6).
So in the conditioned space, the probability for a length 1 sequence is overwhelming.
By this logic, the answer to “what is the probability that you get a 6 from one throw of a normal 6-sided dice conditioned on that all throws gave 6?” is still 1/6! But it’s 1.
As I wrote, the probabilities in the conditional space are *proportional* to the probabilities in the original space, not equal.
So as a result, in the conditional space, the probability for a sequence of length 1 is at least 1,000/6 times the probability for a sequence of length at least 2.
@Ido
So what is the probability that you get a 6 from one throw of a normal 6-sided dice conditioned on that all throws gave 6?
I would totally make this mistake in a paper!
Do you think the referee would catch it?
I had to simulate it to believe it, and indeed 1.5 is the average.
Below was my approach to the problem, before seeing Paul Cuff’s vastly superior solution.
Let’s think of a fair die as being a uniform distribution over {0,1}x{1,2,3}. If my i^th draw is (a_i, b_i), then the number shown on the die is 2b_i-a_i. Notice that a_i and b_i are independent, and that 2b_i-a_i is indeed uniformly distributed on {1,2,3,4,5,6}.
Now, my sequence of die rolls can be thought of as two independent random variables, where one is an i.i.d. uniform sequence (a_i)_i from {0,1} and the other is an i.i.d. uniform sequence (b_i)_i from {1,2,3}.
Let’s define two more auxiliary random variables: T=min{i: a_i=1} and S=min{i: b_i = 3}. We want to condition on the event that “6”=(0,3) is rolled strictly before time T. Equivalently, we want to condition on the event that S<T. In the event that S<T, the first time a "6" is rolled is exactly S.
So, T and S are independent exponential random variables of expectations 2 and 3, respectively, and we just want to compute E[S | S1, it’s not bad with pen and paper to compute the value E[S | S<t] explicitly, and the conditional expectation turns out to be <2.
Since S and T are independent, the value E[S | S<T] is a weighted average of the above, and so is itself <2. (The series defining E[S | S1, since it’s at least 1 state-by-state (within the conditioning event) and strictly higher with positive probability. Therefore, 0 < E[S | S<T] < 1. Then, the multiple-choice format comes to the rescue, delivering an answer of 3/2.
Whoops, I deleted in my penultimate paragraph. It should read:
“… and we just want to compute E[S | S1, it’s not bad with pen and paper…”
“… and we just want to compute E[S | S<T ]. Given a number t strictly greater than 1, it’s not bad with pen and paper…”
I get 3/2, but instead of the calculations I went through, let me try to give an intuition. Say we just know we rolled the die i times and the first 6 was the last time. Then the probability that all the previous rolls were even is 2/5^(i-1), dropping faster than 1/2^i, which is the likelihood that all rolls were even. So shorter sequences are favored by the conditioning event, making the expectation smaller. As the number of sides increases then, the effect will be diminished, ((n/2-1)/n vs 1/2) and the intuitive answer becomes close to the actual expectation.
:
I think we can provide the following simplest and complete intuitive explanation. Let N be the number of dice rolled to obtain the first 6 and let E the event “all numbers obtained until the first 6 are even”. The probability ratio P(N=k+1 | E) / P(N=k | E) does not depend on P(E) — we don’t even need to calculate P(E). This ratio is equal to P(N=k+1, E) / P(N=k, E) = 1/3 for all k>=1. Hence, we obtain a geometric distribution with failure and success probability p_f and p_s respectively equal to 1/3 and 1-1/3=2/3, whose expectation is therefore 1/p_s=3/2.
On the other hand, if we had instead a 3-sided die with 2, 4, and 6 on its three faces, then we would have a geometric distribution with failure and success probability respectively equal to 2/3 and 1/3, and the required expectation would be 3, i.e., **exactly** the double of the one of the original problem, because the success probability would be **exactly** p_s/2.
If we have a n-sided fair die with n>>1, as n increases then the probability to obtain the first 6 at the first roll, conditioned to having only 2 or 4 before the first 6, approaches 1 and the required expectation approaches 1 too, because shorter sequences are more and more favored by the conditioning event.
3/2 The explanation at the link.
https://drive.google.com/file/d/0BxUf40PyJyBpNFBja1JzanJtUDg/view?usp=sharing
Before conditioning, the probability that we play for
rounds decays like 
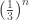(we need roll 2 or 4 every round except the last). Conditioning multiplies by a constant but doesn’t change the exponential decay, so the resulting distribution is the geometric random variable with failure probability 
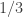, success probability 
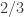and expected time to success 
.
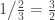Ah well, my take was the same as Paul Cuff’s, it turns out 🙂 I wonder if that is also what Elchanan had in mind when posing it. Anyway, very nice question! (and lovely picture of Elchanan 🙂 )
As for the English dilemma, there is the well-known saying “Never say die!”….
Let p be the probability that a sequence terminates with a 6 before an uneven number occurs (the conditioned space).
Then p = 1/6 * (2/6)*p -> p = 1/4 (either it hits 6 on the first throw, or it has hits 2/4 and you face the same probability again).
So, what is the probability, given the condition, that we hit six on the first throw?
Without the condition, that would be 1/6, but the condition says only 1/4 of the alternatives are possible, thus the probability ends at 2/3.
The expected value of a geometric distribution then gives us E=3/2.
Should say: p = 1/6 + (2/6)*p → p = 1/4
For me, die is the only possible singular of dice, even the f it sometimes sounds awkward. “One dice” just sounds ignorant.
Probability of getting 1/6 on first throw with conditions is 1/3/1/2 or 2/3. Note that any sequence ending with 1/6 can be reversed to begin with 1/6 so E(x)=1/(2/3)=1.5
Where does “1/3/1/2” come from? The answer is correct, I just don’t follow the method.
What would your method give you for an 8-sided die, rolled until getting an 8, conditioning on even results only?
Here’s some empirical support for 3/2:
def throws():
“Return a random list of throws, ending when you get 6.”
die = random.choice((1, 2, 3, 4, 5, 6))
return [die] if (die == 6) else [die] + throws()
mean(len(seq) for seq in (throws() for i in range(100000))
if all(d % 2 == 0 for d in seq))
1.497997
I am totally confused by this.. isn’t a simple intuitive way to think about this be: if the average of hitting 6 on a dice is 3 throws, then hitting a 6 on a dice where you can only hit evens (i imagine a weighted die) be 1.5 because of the halved possibilities? Am I missing something?
The average time it takes to roll a six is 6 throws, not 3. A good way to see this is to imagine a six-million-coin-toss experiment and divide it into runs that end with a six (with an unfinished run at the end that we may ignore). Since there are about a million 6’s in tbe experiment, there are about a million runs, and since tbe total length of the runs is six million, the runs have an average length of 6.
Here’s how I got intuition about this: imagine that we’re throwing darts uniformly at an n*n board. What’s the expected number of throws until we hit the top left corner, conditioned on always hitting the topmost row until that time? In this case, it feels obvious that the conditioning on always hitting the topmost row is so “stressful,” that the conditioned process wants to “get that part over with as quickly as possible,” and just hit the top left corner so it can get on with hitting the rest of the board. Therefore the expected number of throws will be less than n.
Die vs dice is just your standard-issue conflict between the rules of English as they are and as they would be were we designing them from scratch—like “always put the period inside the quote.”
Here is a nice variant:
You toss a die 10,000 times. What is the expected number of tosses until reaching six (the toss giving six is counted) conditioned on the event that six is reached and all tosses after reaching six are even.
You may consider infinite number of tosses if you fill comfortable with infinite probability spaces.
Very cute.
The infinite case isn’t well defined, I think, since the event that all (infinitely many) tosses after the first six are all even will have probability zero. There is also no convergent limit for the answer as 10000 -> infinity.
However, if you change the condition to the symmetric “six is reached, and all tosses *before* the *last* six are even”, then the conditional expectation / distribution will converge meaningfully as the number of tosses is increased, even though the limit event will still have probability zero.
Another nice variant is to compute just the probability that the first toss gives 6.
“You toss a die until you get 6. What is the probability that you got 6 in the first toss conditioned on the event that all tosses gave even numbers?”
There is a story about a a mathematician who tried to explain intuitively to her husband that the expected number of tosses until reaching “six” is six, and the explanation worked so well that he was convinced that the expected number of tosses until reaching “five” is five.
J. Michael Steele calls this “first step analysis”. Let c be the probability that 6 appears before 2 and 4, given that 6 appears before 1,3, and 5. Then c=5!/(6!/4)=2/3 just by counting the ways to order 1,…,6. Now the expected number, E, satisfies E = 1(c) + (1+E)(1-c) since either we immediately get a 6, or else we expect 1+what we originally expected. Solving for E gives E=1/c=3/2.
This is fascinating example with so many lessons to learn 🙂 Although many people before me posted right solutions to the problem, what I was missing is a ‘rigorous’ wrong solution that arrives to the wrong answer 3 (and its correction). I think that a wrong solution, with the error in it pointed out, is just as instructive as a completely independent solution that arrives to the right answer.
The lesson to be learned is that conditional expectations should be treated with care 🙂
I compiled a small note about this (http://bit.ly/2xUj9bX), so I won’t have to explain this to students after they get this example on conditional expectations. Thanks for the post!
Pingback: Exploring Elchanan Moddel’s fantastic probability problem with kids | Mike's Math Page
Pingback: Exploring Elchanan Mossel’s fantastic probability problem with kids | Mike's Math Page
I wrote a computer to check that the expected value is 1.5 and the program itself lends itself to an easy proof. The program generates random die throws keeps counts of 2’s and 4’s until one sees a six. If a 1, 3 or 5 shows up you can throw away that run and it resets the counter to zero.
Looks at the sequence of die throws generated by the program. Look at each 6. If the previous throw had value 1, 3, 5 or 6, the length of the sequence generating the 6 is 1. So there is a ⅔ probability of the sequence generating 6 in one step. In general the probability of that sequence having length i is (⅓)^(i-1) ⅔. Summing that series gives the expectation 3/2.
Just for fun, here is a wrong “intuitive” way to get to 3/2 🙂
If we had a fair die with only even faces (2,4,6) on it, the expected time to reach 6 when rolling it would have obviously been 3. But our conditioned die isn’t like that – on every toss, the apriori die only has a probability of 1/2 to behave as an “even die”, and probability 1/2 to get an odd result and have the trial thrown out. So, because the trial must not be thrown out before reaching 6, we should reach it more quickly than the “even die” does. Since we have a probability of 1/2 of terminating instead of rolling the even die, we should reach it 2 times more quickly, i.e. on average in 3/2 tosses.
The last line in the above “computation” doesn’t really have any basis, though. In fact, for a 2N-sided die, the same argument as above would tell us that the average number of tosses to reach 2N conditioned on all tosses being even should be a N/2, whereas it is actually 2N/(N+1). These two values agree (miraculously) only for N=3.
Many thanks, everybody, for the interesting comments!
I found 1.5 to be the limit, contrary to my intuition. I computed it this way, in J
roll=: [: }. (],?@[)^:(<:@[ ~: {:@])^:_~
filter=: #@[ = #@(#~ 2&|)
(+/%#)@(#~ *) ((filter*#)@roll)"0 (1e6# 6)
Here’s another way to think about it (but not all that different deep down). Suppose you have a die with just the numbers 2,4,6 on it. You repeatedly roll the die until you get a six. Obviously the expected number of rolls you need is three. But if you change the rules so that before each throw you toss a coin and if it comes up tails the game is aborted, then things change. Initially, the probabilities of the various outcomes were 1/3, 2/9, 4/27, 8/81, …, but afterwards they change to 1/6, 1/18, 1/54, …, which is proportional to the probabilities you get from a geometric distribution with parameter 2/3. And this is equivalent to the question asked. Leaving aside what the result of the calculation is, this makes it obvious that the expectation is going to be different, and indeed that it will go down. But in fact it also makes it clear that in going from the “naive” wrong answer to the correct answer, one is dividing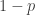
by 2, where 
is the parameter in the geometric distribution, so 
goes up from 1/3 to 2/3 and the expectation goes down from 3 to 3/2.
I should say that I fell right into the trap, and am writing this only after learning the right answer and reading some of the comments above. (But in my defence, I didn’t have time to think about the question for long, and I thought it was likely that I was falling into a trap, since otherwise the question wouldn’t have been asked in the first place.)
If one conditions on the event that all the throws gives an even number, then we can safely ignor odd values and the problem is equivalent to considering a dice with only values 1,2,3 and looking for the expected time until the first 3 shows off, that is the expected length of an initial sequence avoiding a value.
That is exactly the very plausible argument that turns out to be wrong and that makes this paradox such a good one.
I “guessed” 1.5, but I think the correct answer as far as English is standardly spoken is actually 3. The reason is not die vs. dice, but instead the word “until.” That implies a stopping time. The J. Michael Steele version is clearly not a stopping time and so is well posed and the calculations make sense and are beautiful and intuitive. So the only sensible version as far as making it a stopping time is: “throw a dice if isn’t even discard it. Keep throwing until a 6 is achieved. You will be waiting 3 tosses.” This uses the word “until” as a stopping time. Can someone describe the problem as given in a similar fashion? It would have to read something like:
“Consider sequences which are even before the first 6 is rolled, and any number 1-6 afterwards. Each such sequence is given equal probability. How long do you wait UNTIL a 6 is rolled?”
This would then be using the word until as a stopping time and hence not be confusing given standard English usage!
If I’m not mistaken, there are complexity classes which involve conditioning on the path. They also get some “curious” results and can compute stuff really fast!
In my opinion, this “paradox” mainly stems from the phrasing.
It becomes much less “paradoxical” when rephrased to:
What is the expected length $\ell$ of a sequence of dice throws that is constructed under the following rules:
When a 1,3 or 5 is rolled, the sequence is reset to the empty sequence.
When a 2 or 4 is rolled, the sequence is appended by said number.
When a 6 is rolled the sequence is appended by 6 and the construction is finished.
In this case, Lance Fortnow’s explanation is excellent and the expected length $E(\ell)$ is given by
$$\sum_{\ell} \ell \cdot 2/3 \ cdot (1/3)^{\ell -1}$$ which is $1,5$.
I didn’t give any interpretation of my calculation of the probability in my earlier comment The calculation can be found here http://bit.ly/2gPSw10. I will provide that now.
The key to understanding this paradox is to realize that the objects of interest are the sequences of trials and not the individual trials. At each trial a decision is made to discard the sequence if the outcome is odd, terminate the experiment if the outcome is a six, or continue the experiment if the outcome is a 2 or a 4. These decisions are based on the entire history up to that point not just the trial under consideration.
Continue reading. https://drive.google.com/file/d/0BxUf40PyJyBpYWhuMUo2bVR0NlU/view?usp=sharing
Under the same hypotheses (all evens), the probability that the sequence has length 1, i.e. is a single 6, is 2/3. Weird at first since in the larger even space the probability of a length one sequence is 1/6.
Let X be the time to get the first 6, and A be the event that all the throws till the first 6 are even. For any n \ge 0,
P(X=n | A)
= P( [X=n] \cap A) / P(A)
= (2/6)^{n-1} (1/6) / P(A)
= c (1/3)^{n-1} , for some constant c.
Therefore, the conditional distribution of X given A is Geometric (2/3), and hence E(X|A) = 3/2.
The following is an easy way to see why the naive intuition fails. Letting A be the event that all throws till the first 6 are even, observe that
P( A | the first throw is 2) = P(A).
This becomes more obvious if A is interpreted as “the first 6 comes before the first odd number”. In other words, A is independent of the event that the first throw is 2, and therefore conditioned on A, the probability that the first throw is 2 is 1/6. Hence, conditioned on A, in each trial, 2, 4 and 6 are not equally likely. In fact, 6 is more likely than 2 and 4.
“P( A | the first throw is 2) = P(A)”
This is not true. For a specific length, P(A) depends of the probability of each roll, from 1 to n. So the first roll has some probability, less than 1.
But the condition you added “first throw is 2” makes the probability of the first throw equal to 1. We are now sure that the first throw led to another one, since we are sure that the outcome was 2.
To calculate (remember that we only have even numbers):
P(A) = 1/3 * (2/3) ^ n-1
P(A | the first throw is 2) = P(A AND first throw is 2) / P (first throw is 2) =
= 1/3 * 1/3 * (2/3) ^ n-2 / 1/3 = 1/3 * (2/3) ^ n-2
(so one of the 2/3 factors turned into a 1)
The mistake here is that P(A) is not a constant. It depends on the length. So for n=1 then P(A) = 1/2, for n=2 then P(A) = 1/4 and so on. To generalise, P(A) = (1/2) ^ n.
Note also that each n generates its own sample space. So you cannot calculate P(A) over some infinite sample space having infinite probability. You need to calculate it for each n.
So what is the probability that we get a 6 from one throw of a normal 6-sided dice conditioned on the event that all throws gave 6?
1.5. It isn’t very different from the expected number of throws until you hit a 3 using a three sided die.
Pingback: Random Storm Thoughts | A bunch of data
Maybe it could be useful if somebody can easily provide us with a random sequence of 200 tosses of a fair dice.
@GilKalai: a bunch of radioactive dice tosses: https://www.random.org/integers/?num=200&min=1&max=6&col=8&base=10&format=html&rnd=new (new sequence every reload)
Let b be a dice outcome in {1,3,5,6}. By symmetry, conditioned on having a sequence of dices of only 2’s and 4’s before reaching the first b, the expected sequence length up to and including the first b is the same for any b in {1,3,5,6}.
Now consider the expected time it takes for a random sequence of dices to first reach one of the values in {1,3,5,6}. This value is clearly 3/2 since its the expected value of a geometric random variable with probability of success 4/6. Furthermore, this value is the average of the previous expectations, which finishes the proof.
“Now consider the expected time it takes for a random sequence of dices to first reach one of the values in {1,3,5,6}. This value is clearly 3/2”.
This is true. However, the problem says “roll until you get a 6” and not “roll until you get a 1 or a 3 or a 5 or a 6”. These are two different problems. Obviously it is easier to reach your target if the target is four different sides of the die rather than one side.
When we throw a infinite sided die until you get 6, the expected number of throws (including the throw giving 6) conditioned on the event that all throws gave even numbers is 2 !
Pingback: A Probability Puzzle That You’ll Get Wrong | Math with Bad Drawings
What a lot of mental exercise for the simplest of probability problems!
It doesn’t matter what came up in the previous throws. That’s right – nothing that happened in the past has any influence on the result of the next roll. This assumes, of course, that the die is fair and rolling surface is even.
Every roll carries a 1/6 probability of turning up any number. That’s all there is to it.
This example was presented in my graduate-level statistics class 40 years ago. The answer hasn’t changed, but the number of wrongs answers seems to have grown, though by what factor I couldn’t guess.
Pingback: Monty Hall (1921-2017) and His Problem | A bunch of data
The problem with the intuition is that we think sh are changing the probability space whereas we are not, we are just now rejecting more sequences (e.g. we now treat 16 like we did 22 before).
well the answer seemed to be 3 to me as well but it’s not I don’t know how and why but I simulated 1000 rolls in java and I found out this from 2 simulations :
no. of rolls to get to 6 with the given conditions frequency (i) frequency(ii)
=1 494 504
=2 252 252
=3 136 105
=4 55 66
=5 26 42
=6 17 12
>6 20 19
From this data, it is promising that it is somewhere between 1-2 (1.5 is the correct answer)
The problem here is that you started the simulation with incorrect assumptions. You probably simulated the dice to have 1/6 possibility for each of the numbers 1,2,3,4,5,6. This would be ok if it wasn’t for the condition. The condition clearly says that P(1)=P(3)=P(5)=0 (ie. these outcomes will NEVER happen). So you need to simulate the dice to only have outcomes 2,4,6 with some probability each, adding up to probability 1. And because there is no information that tells us otherwise, the probabilities of these are equal and they have to be 1/3.
Try it, and you will most probably find the no. of rolls to be close to 3.
Pingback: Links 23 March 2018 – Power Word: Real Name
I guess my question is, why is everyone getting this wrong from all sides of the fence? The answer is neither 3 nor 1.5, and that’s patently obvious if you actually do the math behind it.
Probability in calculating consecutive results is not done by averages. Nor is it done by Geometric Distribution (for small numbers). And if anyone would have just stopped to do the math, they would have realized this a lot sooner.
Nowhere in the problem does it state that we can’t get repeating results. Nor does it state that we will get an even distribution of numbers. This makes all of these previous methods completely invalid, because the mechanisms behind the problem do not place even weight on all distributions of all results (hitting a 6 invalidates further results). Just run the numbers manually to see what happens.
Odds of first die being 6: 1/3 (cumulative odds 3/9)
Odds of first die being 2,4: 2/3
Odds of second die being 6: 1/3 (cumulative odds: 2/9 + 3/9 – Note, in order for 1.5 to be true, this would need to be 3/9 + 3/9)
Odds of second die being 2,4: 2/3
Odds of third die being 6: 1/3 (cumulative odds: 4/27+2/9+3/9
Odds of third die being 2,4: 2/3
At this point, there’s still nearly a 30% chance that we haven’t rolled a 6. Obviously, the phrase “expected number” would imply, in my mind, a probability that meets or exceeds 50%. But 1.5 has a sub-50% chance to roll a 6 (it’s around 45~%).
We can validate this by allowing odd numbers, and seeing if that holds true after an even number of rolls.
1-(5/6)(5/6)(5/6) = 42.13% chance to roll a 6 after 3 rolls.
1-(5/6)(5/6)(5/6)(5/6) = 51.77% chance to roll a 6 after 4 rolls.
Obviously, if you roll a pseudo-infinite number of rolls, the probability will normalize over time if you’re trying to count the average number of times you roll a specific number (which is irrelevant, because we’re trying to see how many rolls will get us exactly one 6), but simply ignoring that the probability is *not* normalized will lead to the incorrect answer of 1.5.
The probability that the sequence hasn’t stopped on the n-th throw (either 2 or 4 on each throw) is (1/3)^n. The probability that the sequence does stop is 1-(1/3)^n. Then we may choose among 1,3,5,6 with a probability of 1/4 to get 6.
So p(n)=(1/4)*(1-(1/3)^n) which tends to 1/4 for large n.
The expected value Sum(n*p(n)) is infinite.
Reblogged this on 1. Mathematics Scouts.
I think the easiest way here is to derive the PMF of the number of rolls until a six (say X), given that all rolls before that are 2 or 4 (say the event E). That is Pr(X = x|E) = Pr(X = x, E)/Pr(E). The numerator is clearly Pr(X = x, E) = (2/6)^(x-1)*1/6. For the denominator, condition on the value of X, i.e.,
Pr(E) = \sum_{i=1}^\infty Pr(E | X = i)*Pr(X = i)
= \sum_{i=1}^\infty (2/5)^(i-1) * (5/6)^(i-1)*(1/6)
= (1/6) * \sum_{i=1}^\infty (2/6)^(i-1)
= (1/6) * (1/(1 – 1/3)).
Therefore, Pr(X = x|E) = (2/3) * (1/3)^(x-1), which is geometric with success probability 2/3, and hence expected value 3/2.
The mistake here is calculating the denominator over a sample space with infinite probability. So we are creating a massive sample space {1, 2, 3, 4, 5, 6, 11, 12,…,66, 111, 112… } with total probability of infinity. The outcomes of the experiment ending in a single roll (ie. 1, 2, 3, 4, 5, 6) have a probability of 1/6 each and a total probability of 1. The outcomes of the experiment ending in two rolls (ie. 11, 12,…66) have a probability of 1/36 each and a total probability of 1. So the total probability of the above massive sample space (for infinite lengths) is infinite, thus is an incorrectly defined sample space. It needs to be broken down per length, eg:
For length 1 the sample space is {1, 2, 3, 4, 5, 6}
For length 2 the sample space is {11, 12, 13,…66}
Then the conditional probability formula needs to be calculated for one of these sample spaces, so for a specific length. The denominator is different, depending on the length.
Here is a correct and intuitive way to understand it. Suppose you roll a die about a million times and record the rolls as one long string of numbers. Every 6 in there is the end of a legal sequence of some length L. The probability that the number before the 6 is 1,3,5 or 6 is 4/6. In this case the 6 is the end of a legal sequence of length 1, i.e., only the 6 itself. So the probability that L=1 is 2/3.
That leaves probability 1/3 for a longer sequence with L being 2 or more when there is at least one 2 or 4 preceeding the 6. The expected length is thus L = 2/3.1 + 1/3.(2 + TF) where TF is the expected length of the run of further 2’s and 4’s preceeding the 2 or 4 we already found, including run length 0 if there are no further 2’s and 4’s.
Next we determine TF, the expected length of a run of 2’s and 4’s only. The probability that the run length is 0 is 2/3. The probability that the run length 1 is (1/3).(2/3) since we first need a 2 or 4, and then something that is not a 2 or 4. That leaves probability (1/3).(1/3) for a run length of 2 or more 2’s and 4’s. For the “or more” part we can use TF itself again. This leads to TF = (2./3).0 + (1/3).(2/3).1 + (1/3)(1/3)(2 + TF). Rewriting we get (8/9)TF = 2/9 + 2/9 = 4/9 so that TF = 1/2. Substituting TF in L we get expected sequence length L = 2/3 + 1/3.(2 + 1/2) = 2/3 + 5/6 = 1.5.
“The probability that the number before the 6 is 1,3,5 or 6 is 4/6”
The above is only true for the UNconditioned space (of an individual roll): that is {1, 2, 3, 4, 5, 6} with probability 1/6 each. So rolling a 1 or 3 or 5 or 6 has indeed the probability of 4/6.
But in the conditioned space, P(1)=P(3)=P(5)=0. That modifies the space as {2, 4, 6} with some probability each – adding up to 1. Since there is no information that tells us otherwise, the probabilities of these three outcomes are equal and are now 1/3. So the above probability is now 1/3.
This is a simple and intuitive explanation of the result. Let N be the number of dice rolled to obtain the first 6. Within the conditioned probability space, we have P(N=k+1) = P(N=k)/3 for all k>=1, which implies that P(N=1)=2/3 so that the summation over all k>=1 is equal to 1. Hence, we have a geometric distribution with a probability of success p=2/3, whose expectation is therefore 1/p=3/2.
“Within the conditioned probability space, we have P(N=k+1) = P(N=k)/3 for all k>=1”
The above is only true for the UNconditioned space (of an individual roll): that is {1, 2, 3, 4, 5, 6} with probability 1/6 each. So rolling a 2 or a 4 is indeed 1/3.
But in the conditioned space, P(1)=P(3)=P(5)=0. That modifies the space as {2,4,6} with some probability each – adding up to 1. Since there is no information that tells us otherwise, the probabilities of these three outcomes are equal and are now 1/3. So the probability of rolling 2 or 4 is now 2/3.
Pingback: Greatest Hits 2015-2022, Part I | Combinatorics and more
I found this very interesting but I am surprised by how many people believe that the answer is 3/2. Also lots of complex calculations that include numbers 1, 3 and 5, and experiments where unconditional probabilities of a die are used for a problem with conditional probability. Furthermore, trials that is not using the conditioned sample space but the original, with some results being tossed out later (reminds me of the boy-girl paradox).
The condition is clear: numbers 1,3,5 can NOT happen. They will NEVER appear. There are no “failed” results, the condition is a GIVEN, a FACT. The conditioned sample space is simply {2,4,6} with some probability each. And since there is no information that tells us otherwise, these numbers have now an equal probability of 1/3. The expected number of rolls is the reciprocal of this, so 3.
The same can be calculated using formulas, although it is easily understood intiutively. For a given roll “n”:
P (roll to 6 | even numbers) = P (roll to 6 AND even numbers) / P (even numbers) = 1/6 * (2/6) ^ (n-1) / (1/2) ^ n = 1/3 * (2/3) ^ (n-1) which is the formula for the 3-sided die.
From reading all the comments, I realised that most people did the same mistake: they created a massive sample space {1, 2, 3, 4, 5, 6, 11, 12, 13,…. 111, 112….} with total probability of infinity. The outcomes of an experiment ending in a single roll (ie. 1, 2, 3… 6) have probability of 1/6, so probability 1 in total. The outcomes of an experiment ending in two rolls (11, 12, 13… 66) have probability of 1/36 so also a total probability of 1. So the total probability of the above massive sample space (for infinite lengths) is infinite, thus it is an incorrectly constructed sample space. It needs to be broken down per length, eg.
For length=1 the sample space is {1, 2, 3, 4, 5, 6}
For length=2 the sample space is {11, 12, 13,…. 66}
And all formulas should be calculated separately for each sample space (ie. for each length). Only the “Expected number of trials” is calculated over all the lengths (once the conditional probability per length is calculated in advance).