Both trees in general and random trees in particular are wonderful objects. And there is nothing more appropriate to celebrate Russ Lyons great birthday conference “Elegance in Probability” (taking place now in Tel Aviv) than to test your intuition, dear reader, with questions about probability and trees.
Model 1: consider a set of n vertices {1,2,…,n} and a random spanning tree T on these vertices.
Test your intuition: What is the behavior of the diameter of T?
The diameter of a graph G is the maximum distance between pairs of vertices of G. The distance between a pair of vertices is the length of the smallest path between them. (For a tree there is a unique path.)
The answer and two follow up questions are below the fold.
Answer for model 1: the diameter of a random tree behaves like 
Model 2: assign each edge {i,j} a real number between 0 and 1 uniformly and independently. Let T be the minimum spanning tree.
Test your intuition: What is the behavior of the diameter of T?
(We refer to the diameter of T regarded as an abstract graph.)
Is the exponent of n larger or smaller than 1/2? What is the exponent?
Model 3: start with an m-gon 
Test your intuition: What is the behavior of the diameter of T?
Is the exponent of n larger or smaller than 1/2? What is the exponent?
Combinatorics and more 
Please define “diameter”
Dear Nick, thanks for asking.
The diameter of a graph G is the maximum distance between pairs of vertices of G. The distance between a pair of vertices is the length of the smallest path between them. (For a tree there is a unique path.) I added the definitions to the post.
Model 2: n^1/3
Nick, what is your intuitive reason for 1/3?
The fact that I wrote a paper on something that seems to be equivalent 🙂
I guess the fact that it seems to be equivalent is the intuitive part
See Phys. Rev. E 81, 021130 (2010) and https://arxiv.org/abs/1301.1667 for the rigorous part
Pingback: Elchanan Mossel’s Amazing Dice Paradox (answers to TYI 30) | Combinatorics and more
Can you elaborate on what ‘random’ means in model 1? Do you pick a spanning tree from the set of all spanning trees with equal probability?
Dear Vincent, yes this is what I mean.
Pingback: Some Mathematical Puzzles that I encountered during my career | Combinatorics and more
Dear Gil,
The answer from model 2 seems to be in the following paper:
The scaling limit of the minimum spanning tree of the complete graph, by Louigi Addario-Berry, Nicolas Broutin, Christina Goldschmidt and Grégory Miermont, Annals of Probability 45, 5 (2017), pp.3075-3144.
If M_n is the minimum spanning tree of the complete graph with i.i.d. U[0,1] edge-weights, d_n is the graph distance in d_n and \mu_n is the uniform measure on the vertices, then there exists a random binary R-tree (M, d) endowed with a measure \mu such that
(M_n, n^{-1/3} d_n, \mu_n) \to (M, d, \mu)
in distribution as n \to \infty, in the sense of the Gromov–Hausdorff–Prokhorov topology. (M has Minkowski dimension 3 almost surely, and so is not the Brownian CRT.) In particular, this result implies that if D_n is the diameter of M_n then
n^{-1/3} D_n \to D
in distribution as n \to \infty, for some a.s. finite random variable D, which is the diameter of the metric space (M, d).
(In his comment, Nick Read gives a link to Louigi’s paper on the local weak limit of M_n, but that tells us nothing about the convergence of the diameter; I guess he meant to link to the above paper instead.)
Julien: No, I linked to the paper I intended. That paper and the earlier one by Jackson and myself show that the mass within graph distance n on the random MST on the complete graph or on the Cayley tree or PWIT scales as n^3 when n << N = number of vertices. It is true that this is a local property, unlike the diameter, but my intuition was that the former implies (e.g. by setting n^3=N), that the diameter scales as N^{-1/3}—that is assuming one exponent describes both. It is nice to know that the intuition is correct—and Gil did ask for intuition.
Many thanks for the comments Nick and Julien,
Regarding Model 2 let me also mention the 2006 paper The Diameter of the Minimum Spanning Tree of a Complete Graph by Louigi Addario-Berry, Nicolas Broutin, and Bruce Reed. It gives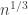
settling a 1997 conjecture of Frieze and McDiarmid.
Dear readers, can you guess the exponent in Model 3?
Frieze and McDiarmid 1997 asked: “is [the diameter] $n^{1/2}$?”
Dear Nick, I see, so they answered the question in the negative! (A little like this comment . ) Is the paper by Addario-Berry, Broutin, and Reed, the earliest where the exponent 1/3 appeared? Is your paper that you mentioned the one where Newman old prediction is confronted? Is the 1/3 1/2 gap relevant to that conflicting predictions?
Here is the arxived version of the paper by Jackson and Read.
Theory of minimum spanning trees I: Mean-field theory and strongly disordered spin-glass model
T. S. Jackson, N. Read
Gil, I don’t know the answer to your first question, though A-B, B, R do not mention any earlier results other than the question of Frieze and McDiarmid (as far as I can see).
You raised the question of the old Newman-Stein work, Phys. Rev. Lett. 72, 2286 (1994),
to which my paper with Jackson was a response. They studied the minimum spanning tree on Z^d, not the complete graph, though their argument involved invasion percolation on the Cayley tree. In terms of our discussion here, their argument would imply mass (number of vertices) within radius n scaling as n^4, or presumably diameter N^{1/4}. Really they found an upper bound on the former exponent. So we disagreed with them, finding n^3. (This is a paraphrase of the subject line of an email I once sent to Russ Lyons.)
So no, they differed in the other direction (though at one point they seemed to say n^2, which is the result for invasion percolation, but was an oversight).
Thanks for posting the arXiv ref for our paper.
The videos for RussFest can be found here: https://www.youtube.com/playlist?list=PLCdNC0RPzb1GtdIE5RhcTw5obOT2tbgCx