Stefan Steinerberger: The Ulam Sequence

Posted on April 12, 2016 by Gil Kalai

This post is authored by Stefan Steinerberger.

The Ulam sequence

1,2,3,4,6,8,11,13, 16, 18, \dots

is defined by starting with 1,2 and then repeatedly adding the smallest integer that is (1) larger than the last element and (2) can be written as the sum of two distinct earlier terms in a unique way. It was introduced by Stanislaw Ulam in a 1962 paper (`On some mathematical problems connected with patterns of growth of figures’) where he vaguely describes this as a one-dimensional object related to the growth of patterns. He also remarks (in a later 1964 paper) that `simple questions that come to mind about the properties of a sequence of integers thus obtained are notoriously hard to answer.’ The main question seems to have been whether the sequence has asymptotic density 0 (numerical experiments suggests it to be roughly 0.07) but no rigorous results of any kind have been proven so far.

A much stranger phenomenon seems to be hiding underneath (and one is tempted to speculate whether Ulam knew about it). A standard approach in additive cominatorics is to associate to the first N elements of a sequence a_1, a_2, \dots, a_N a
function

 f_N(\theta) = \exp{(a_1 i \theta)} + \exp{(a_2 i \theta)} + \dots + \exp{(a_N i \theta)}

and work with properties of f_N. If we do this with the elements of the Ulam sequence and plot the real part of the function, we get a most curious picture with a peak around
 \theta \sim 2.571447\dots

pic1

Such spikes are generally not too mysterious: if we take the squares 1,4,9,16, ... we can observe a comparable peak at \theta = 2\pi/4 for the simple reason that squares are \equiv 0, 1 (mod 4). However, here things seem to be very different: numerically, the Ulam sequence does seem to be equidistributed in every residue class. Due to 2\pi-periodicity, the function f_N only sees the set of numbers

\left\{ \theta a_n~\mbox{mod}~ 2\pi: 1 \leq n \leq N\right\}

and it makes sense to look at the distribution of that sequence on the torus for that special value \theta \sim 2.571447\dots. A plot of the first 10 million terms reveals a very strange distribution function.

pic2

The distribution function seems to be compactly supported (among the first 10 million terms only the four elements 2, 3, 47, 69 give rise to elements on the torus that lie outside [\pi/2, 3\pi/2].) The same phenomenon seems to happen for some other initial conditions (for example, 2,3 instead of 1,2) as well and the arising distribution functions seem to vary greatly.

 

Question 1: What is causing this?

Question 2: Are there other `natural’ sequences of integers with that property?

 

See also Stefan’s paper  A Hidden Signal in the Ulam sequence .

Update: See also Daniel Ross’  subsequent study of Ulam’s sequence, presented in Daniel’s sort of public ongoing “research log”.  (“It includes a summary at the top of the most interesting observations to date, which usually lags a couple weeks behind the most current stuff.”) 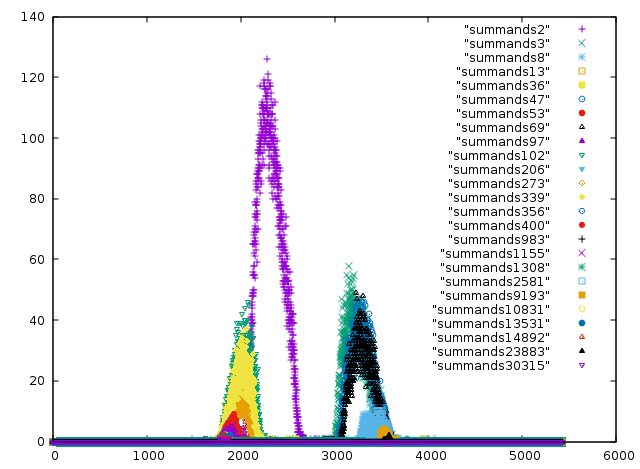pic3

This entry was posted in Guest blogger, Open problems and tagged , . Bookmark the permalink.

9 Responses to Stefan Steinerberger: The Ulam Sequence

  1. Florian says:
    April 12, 2016 at 2:58 pm

    Very interesting – Thanks! The link seems to lead to a different paper, probably the link should be

    Click to access 1507.00267v5.pdf

    Reply
  2. Gabriel Nivasch says:
    April 12, 2016 at 3:40 pm

    What happens if you start with a different initial subsequence (instead of 1,2)? Do you seem to “converge” to the same behavior as the Ulam sequence?

    Reply
  3. Gil Kalai says:
    April 14, 2016 at 7:59 am

    Dear Florian and Gabriel, thanks for the comments. (I corrected the link.)

    Reply
  4. Philip Gibbs says:
    April 14, 2016 at 10:50 am

    Following Stefan Steinerberger surprising observation on this signal in the Ulam numbers I was able to make use of it to develop a fast algorithm for computing the sequence (see the reference in Steinerberger’s paper). With Jud McCranie who had previously been involved in calculating the sequence, we were able to calculate the first 28 billion numbers. The algorithm is limited by memory rather than time constraints so the sequence can be regenerated quickly if anyone has any specific computational studies they want to perform. I am too busy to do much more at this time but can provide Java Code if anyone is interested.

    I think one thing makes this particularly interesting is a comparison with the harmonic structure in the sequence of logarithms of primes which is of course a matter of intense interest. Both the log primes and the Ulam sequence are defined by additive rules. Perhaps there is something in common in the way harmonic structure emerges from these pseudo random processes.

    Reply
  5. Daniel says:
    April 14, 2016 at 11:44 pm

    This is a really neat observation!

    A word about the colourful breakdown of the distribution: Every Ulam number a can be written uniquely as a sum of two smaller Ulam numbers b and c (say b less than c), the summands of a. It turns out that almost all Ulam numbers have as a summand something from a limited set, which includes 2, 3, 47, 69, 102, 13, 36, and some more. If we take any x from that set and plot only Ulam numbers that have x as a summand, we get an interestingly clean peak. As x ranges over the set, we get further peaks that seem to comprise the original distribution.

    If we instead plot, for any x, the set of Ulam numbers y such that x+y is an Ulam number (that is, we plot the “complements” of x, rather than the things with x as a summand), these peaks seem to line up. See https://github.com/daniel3735928559/wip-ulam/raw/master/figs/shifted_summands_mod_5422.png

    Gabriel: The phenomenon seems to exist for other pairs of initial values u, v as well, as is mentioned at the end of the post. However! For certain families of initial values u, v (e.g. 2, 2n+3 or 4, 4n+1) it is known that there are actually only finitely many even terms in the ensuing sequence! This entails, among other things, that the sequence of consecutive differences is periodic, so these sequences are entirely predictable. The phomenon here could maybe be seen as a generalisation of this for other starting conditions? For e.g. the sequence starting 2, 5, there would be a massive spike at theta = pi, corresponding to a non-uniform distribution mod 2.

    Reply
  6. Philip Gibbs says:
    April 15, 2016 at 11:04 am

    It helps to think of an Ulam sequence as an almost sum-free set. If there is only one way to write each number as a sum of previous numbers then that is a statistically low number compared to what you would have for a random sequence with a given finite density. Calkin and Erdos described a class of aperiodic sum-free sets where all elements of the set taken modulo a real parameter lie in the middle third of the range interval.

    Click to access S0305004100074600.pdf

    This is very similar to what we see in the Ulam sequences except that there are rare outliers which form the unique sums. Even the periodic cases fall into this pattern with the parameter equal to 2 so that most numbers are odd with a finite number of even outliers.
    The question is, does this pattern always emerge for any given starting point, and why?

    Reply
    • Philip Gibbs says:
      April 16, 2016 at 10:16 am

      Perhaps someone knows answers to the following two questions that I think are relevant to Steinerberger’s observation. Firstly, suppose a sequence of positive integers has the property that the number of ways that each element can be written as the sum of other elements is bounded. Is it then possible to remove a sequence of zero density in the integers such that the remaining sequence is sum-free? Secondly, what can be said of the structure of sum-free sequences of non-zero density in positive integers?

      Reply

  7. Pingback: The Quantum Computer Puzzle @ Notices of the AMS | Combinatorics and more

  8. Pingback: Greatest Hits 2015-2022, Part I | Combinatorics and more

Leave a comment