A Little More on Boolean Functions and Bounded Depth Circuits

Posted on February 24, 2009 by Gil Kalai

 

Boolean circuits

This post (in a few parts) contains a quick introduction to Boolean circuits. It is related to the recent news post about the solution of Braverman to the Linial-Nisan conjecture. In particular, we will describe very quickly a formulation of the NP \ne P problem and discuss some issues about bounded depth circuits.  I hope that this gives a nice introduction to this area for non-experts (written also by a non-expert). Any comments and corrections (especially from experts!) are welcome. I want to mention, in particular, a result by  Benjamin Rossman about finding cliques in graphs for bounded depth circuits that I found exciting.

A. Boolean functions, Boolean circuits and the NP versus P problem.

1. Boolean functions

A Boolean function of n variables is simply a function f(x_1,x_2,\dots,x_n) where the variables x_k take the values +1 and -1 and the value of f itself is also either +1 and -1.

2. Boolean circuits

A Boolean circuit is a gadget that computes Boolean functions. It is built from inputs, gates and an output. We can think about these circuits as follows: On level 0 there are the variables. On level 1 there are gates acting on the variables. On level 2 there are gates acting on the outputs of the gates on level 1. And in level r is a single gate leading to the output of the circuit. The depth of the circuit is this number r. The size of the circuit is the total number of gates.  The gates perform Boolean operations: They can take an input bit and negate it. They can take several input bits and take their OR – this means that the output will be ‘1’ iff one of them is ‘1’. They can take several input bits and take their AND – this means that the output will be ‘-1’ iff one of them is ‘-1’.

3.  the 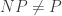NP \ne P problem

Consider a graph G on v  vertices. The question “Does G have a Hamiltonian cycle?”  (a Hamiltonian cycle is a simple cycle containing all the vertices of the graph) is known to be “NP complete”.

Now, suppose that n= {{k} \choose {2}} and associate to every edge of the complete graph on k vertices a variable x_k.

Every graph G corresponds to an assignment of Boolean values to the variables. This correspondence is crucial here and in various other places: the variables associated to the edges of the graph get value ´1´and the variables associated to edges not in the graph get value ´-1´.

The property of graphs on k vertices to be Hamiltonian is described by the following Boolean function f_n on n variables. Every assigenment of values to the variables corresponds to a graph G, and the value of f_n is 1 if and only if the graph G contains a Hamiltonian cycle.   

To prove that NP \ne P just prove that

f_n cannot be described by a Boolean circuit of size s(n) which is bounded above by a polynomial in n.

Is it really the famous P \ne NP problem, you may ask? Well, what we have stated here is a little bit stronger. So if you prove that the Boolean functions representing the graph property “To contain a Hamiltonian cycle” cannot be described by a polynomial size circuit you will prove that NP \ne P and you will have a little change to spare! 

(The assertion that there is no polynomial time algorithm for deciding if a graph with n vertices is Hamiltonian is equivalent to the NP \ne P problem. In the setting of circuits, we talk about the size of the circuit as a substitute to the notion of running time of an algorithm.)

4. A little more on 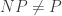NP \ne P. What is NP?

The previous paragraph tells you a formulation of the problem. So you can go ahead and solve it and not worry too much about this paragraph. But the previous paragraph does not tell a few important aspects of the problems and I will mention one aspect now. NP stands for “non-deterministically polynomial” (and not for “not-polynomial” as I thought in my early youth). What does it mean?

The Wikipedea explanation is “a problem is NP as long as a given solution can be verified as correct in polynomial time”. In the world of circuits we have the following description: 

Suppose you want to express the property that a graph has a Hamiltonian cycle in the following way:

You have a Boolean circuit with n+m variables. The n variables correspond to the edges of the complete graph as before. The m variables are new variables y_1,y_2,\dots, y_m and we assume that m is bounded from above by a polynomial function of n. Now we want to describe the property “The graph G is Hamiltonian” by a polynomial size circuit in these n+m variables as follows: If we start with a Hamiltonian graph, we can find an assignment to the variables y_1,y_2,\dots, y_m such that the output of the circuit will be 1. If we start with a non-Hamiltonian graph for every assignment of values to the variables y_1,y_2, \dots, y_m the output of the circuit will be -1.  

Now come the crucial observation: We can do it! We can find a circuit with this property. As before, we let x_1,x_2,\dots, x_n be variables representing the edges of the complete graph with the understanding that x_i=1 if and only if the ith edge is present in our graph G. , But now we take n more variables y_1,y_2,\dots,y_n again representing all possible edges of the complete graph. The y_is which equal to 1 are supposed to correspond to edges of a Hamiltonian cycle in our graph G. So now our circuit in the x_is and the y_is will represent the property that the graph H represented by the y_is is a Hamiltonian subgraph of the graph G represented by the x_is. This can easily be done. This is (more or less) what is meant by saying that the property “to be Hamiltonian” is in NP.

So to say that the graph property “G contains a Hamiltonian cycle” is in NP roughly means that it is possible to prove (or to verify) using a polynomial time algorithm or using a polynomial-size circuit that the graph has a Hamiltonian cycle. The proof consists of presenting a Hamiltonian cycle in the graph. (Again, the circuit notion and the polynomial-time notions are not exactly the same, but let´s ignore it.)

The property “The graph does not have a Hamiltonian cycle” is not known to be in NP and indeed is believed not to be in NP.

5. But what is so special about Hamiltonian cycles.  

The remarkable thing about the Hamiltonian cycle property is that it is a complete problem in NP. A polynomial time algorithm for deciding if a graph is Hamiltonian will give a polynomial algorithm for every problem in NP. (In other words, any problem in NP can be reduced to the problem of deciding if a graph has a Hamiltonian cycle.) There are many, many problems with the remarkable property that they are complete in NP, so there is nothing very special about the problem we have chosen.

6. Reductions

If somebody asks you to describe in one word what theoretical computer science is about, a good word to choose is “reductions”. The art of reductions, the science of reductions,  the practice and engineering of reductions, and  the philosophy of reductions.

7. More general circuits.

We can talk about various other circuits. We can have more sophisticated gates and not just Boolean gates. We can let the variables be real numbers, or elements in some other field, and talk about algebraic gates and algebraic circuits, etc.

8. Asymptotically speaking

The notions we have described are asymptotic. We consider a problem (like the graph property of containing a Hamiltonian cycle) and we study its computational complexity when the number of variables goes to infinity.

B. Bounded depth circuits  

Bounded depth circuits are circuits where the number of levels (the depth) is bounded by a constant. We try to understand the computational power of circuits where r  is bounded, the number of variables n goes to infinity, and the number of overall gates is polynomial in n.  Much can be said about the computational power of bounded depth circuits. Beyond this class things are much harder.

Bounded depth circuits are also fascinating mathematical objects.  —to be continued—

This entry was posted in Computer Science and Optimization. Bookmark the permalink.

7 Responses to A Little More on Boolean Functions and Bounded Depth Circuits

  1. aravind says:
    February 25, 2009 at 4:40 pm

    Hi Gil,

    I look forward to your take on Rossman’s proof. (He has a shorter, informal version of the proof on his homepage which I think I understand.)
    Thanks.

    Reply
  2. Gil says:
    February 25, 2009 at 9:18 pm

    Dear Aravind, I will look at the homepage. I dont promise to explain Rossman’s proof (would you?) but I will explain that I was surprised to learn (and this may also refer to an old reasult by Paul Beam that I did not know) that the Hastad switching lemma is capable to distinguish between polynomial size bounded depth circuits and quasi polynomial size bounded (even larger) depth circuits. (This may have been clear to experts but I did not know of it and I still don’t know it.)

    Reply
  3. Gil Kalai says:
    March 3, 2009 at 9:54 pm

    (Two remarks after talking with Avi)

    I tried to give in the post a very clear and simple mathematical statement which describes the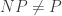 NP \ne P problem. (Or in fact a “slightly” stronger statement.) If you want to think about problems which are not as strong as 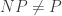NP \ne P but still very very very hard, you can replace “Boolean circuits” by the simpler and familiar notion of “a formula”: Proving that the property “The graph contains no Hamiltonian cycle” cannot be described by a polynomial size Boolean formula in the variables is much beyond reach.

    Indeed, showing that certain functions that can be described by a quasi-polynomial circuits of small depth (even depth two) cannot be described by a polynomial-size bounded-depth circuits go back even to the work of Furst, Saxe, and Sipser. I am not aware of a simple property of a Boolean function that manifests such a separation.

    Reply
  4. Gil Kalai says:
    March 7, 2009 at 11:30 pm

    Some further remarks about the connection between algorithms complexity and circuit complexity can be found here: http://rjlipton.wordpress.com/2009/02/12/is-np-too-big-or-p-too-small/

    Reply

  5. Pingback: Noise Stability and Threshold Circuits « Combinatorics and more

  6. Pingback: Analysis of Boolean functions – week 2 | Combinatorics and more

  7. Pingback: Cody Murray and Ryan Williams’ new ACC breakthrough: Updates from Oded Goldreich’s Choices | Combinatorics and more

Leave a comment