The purpose of this post is to start the polymath10 project. It is one of the nine projects (project 3d) proposed by Tim Gowers in his post “possible future polymath projects”. The plan is to attack Erdos-Rado delta system conjecture also known as the sunflower conjecture. We will start the research thread here. Mimicking a feature of polymath1 I will propose a detailed approach in the next post. Here, I will remind you of the conjecture and some basic known results, mention a few observation and ingredients of my point of view, and leave the floor to you comments.
The Erdos-Rado Delta-system Theorem and Conjecture
A sunflower (a.k.a. Delta-system) of size is a family of sets
such that every element that belongs to more than one of the sets belongs to all of them. A basic and simple result of Erdos and Rado asserts that
Erdos-Rado Delta-syatem theorem: There is a function so that every family
of
-sets with more than
members contains a sunflower of size
.
(We denote by the smallest integer that suffices for the assertion of the theorem to be true.) The simple proof giving
can be found here.
One of the most famous open problems in extremal combinatorics is:
The Erdos-Rado conjecture: Prove that .
Here, is a constant depending on
. It may be also the case that we can take
for some absolute constant C. The conjecture is already most interesting for
. And getting progress for
will already be great.
At least for the delta system conjecture is true. Every two sets form a Delta-system of size two. So
. Can we find more difficult proofs and for weaker statements? The case
will play a role in the context of more general questions.
The best known upper bounds
An excellent review paper is Extremal problem on Δ-systems by Alexandr Kostochka. After an early paper by L. Abbott, D. Hanson, and N. Sauer imroving both the upper and lower bounds, Joel Spencer proved an upper bound of for every fixed
. Spencer also proved an upper bound
for
. (The exponent was improved further to 1/2 by Furedi and Kahn.) A remarkable result by Sasha Kostochka from 1996 is the best upper bound known today.
Sasha Kostochka
A summary of my proposed approach:
I. A more general problem
Given a family of sets and a set
, the star of
is the subfamily of those sets in
containing
, and the link of
is obtained from the star of
by deleting the elements of
from every set in the star. (We use the terms link and star because we do want to consider eventually hypergraphs as geometric/topological objects.)
We can restate the delta system problem as follows: f(k,r) is the maximum size of a family of k-sets such that the link of every set A does not contain r pairwise disjoint sets.
What can we say about families of k-sets from {1,2,…,n} such that that the link of every set A of size at most m-1 does not contain r pairwise disjoint sets? In particular, what is f(k,r,m;n) the maximum number of sets in such a family. We can ask
Question 1: Understand the function f(k,r,m;n).
Question 2: Is it true that , where
is a constant depending on r, perhaps even linear in r.
My proposal is to approach the Delta-system problem via these questions. We note that Question 1 includes the Erdos-Ko-Rado theorem:
(r=2, m=1) Erdös-Ko-Rado Theorem: An intersecting of k-subsets of , when
contains at most
sets.
Here, a family of sets is “intersecting” if every two sets in the family has non empty intersection. The situation for and general
was raised by Erdos-Ko-Rado (who proposed a conjecture for a certain special case), Frankl proposed a general conjecture that was settled by Alswede-Khachatrian. This was a remarkable breakthrough. The case of general r and m=1 is again a famous question of Erdos. The conjecture is that when
,
This is a classic result by Erdos and Gallai (1959) for graphs (k=2), and very recently it was proved for r=3 for large values of
, in the paper On Erdos’ extremal problem on matchings in hypergraphs by Tomasz Luczak, and Katarzyna Mieczkowska, and for all values of
by Peter Frankl.
We want much weaker results (suggested by Problem 2) than those given (or conjectured) by Erdos-Ko-Rado theory, but strong enough to apply to the Delta system conjecture.
II. moving to the multipartite case
A family of -sets is balanced (or
-colored) if it is possible to color the elements with
colors so that every set in the family is colorful.
Reduction (folklore): It is enough to prove Erdos-Rado Delta-system conjecture for the balanced case.
Proof: Divide the elements into d color classes at random and take only colorful sets. The expected size of the surviving colorful sets is .
III: Enters homology
A family of
-sets is acyclic (with Z2 coefficient) if it contains no
-cycle. A
-cycle
is a family of
-sets such that every set of size
is included in an even number of
-sets in
.
Theorem 1: An acyclic family of k-subsets of [n], contains at most sets.
I suppose many people ask themselves:
Question 3: Are there some connections between the property “intersecting” and the property “acyclic?”
Unfortunately, but not surprisingly intersecting families are not always acyclic. And acyclic families are not always intersecting.(The condition from EKR theorem also disappeared in the result about acyclic families.)
Lets ignore for a minute that being acyclic and being intersecting are not related and ask.
Question 4: Is there some “acyclicity” condition related to (or analogous to) the property of not having 3 pairwise disjoint sets? r pairwise disjoint sets?
We know a few things about it.
Question 5: What can we say about families which are acyclic and so are all links for every set A of size at most m-1?
Here under some additional conditions there are quite a lot we can say in a direction of bounds asked for in Question 2.
(We note that one place where a connection between homology and Erdos-Ko-Rado theory was explored successfully is in the paper Homological approaches to two problems on finite sets by Rita Csákány and Jeff Kahn.)
IV) Coloring to the rescue!
Relating acyclicity and being intersecting is not easy in spite of the similar upper bound. We can ask now if for balanced families, there are some connections between the property “intersecting” and the property “acyclic?”
Question 6: Let be a balanced intersecting family of
-sets, is
acyclic?
The answer is yes. Eran Nevo pointed out a simple inductive argument which also extends in various directions. If you have a balanced k-dimensional cycle (mod Z/Z2) then by induction the link of a vertex v (which is also a cycle) has two disjoint sets R and R‘ and taking one of those sets with v and the other set with yet another vertex w yield a disjoint pair. (Each set of size k-1 in a cycle must be included in more than one sets of size k; in fact this is the only fact we are using.)
On technical matters: The project will run over this blog and Karim Adiprasito will join me in organizing it. (Perhaps to make the mathematical formulas appearing better we will move to another appearance.)



Hi Gil, I cannot see some of the equations as it requires me to “log in” to the blog (which I think I am). In any case, great choice for the next polymath project!
Dear Shachar, thanks! I fixed it (I hope)
I hope to leave a more sensible comment soon, but for now let me just point out a small typo at the beginning of the section entitled The Best Known Upper Bounds. At one point you write f(d,r) when I think you mean to write f(k,r).
I’ve just looked up what the middle part of a sunflower, the part with all the seeds, is called, and apparently it is the capitulum. That seems a bit pretentious to use as a mathematical term, but fortunately it is also known as the head. So in this comment if we have sets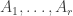 that all contain a set
that all contain a set  and are disjoint outside
and are disjoint outside  , then I’ll call
, then I’ll call  the head of the sunflower and the sets
the head of the sunflower and the sets  the petals. Probably this is standard terminology (certainly I think that is what people commonly mean by petals in this context).
the petals. Probably this is standard terminology (certainly I think that is what people commonly mean by petals in this context).
Your question 2 can then be rephrased as follows. (It’s not necessarily an improvement, but for some reason I find it easier to hold in my head.) How large a collection of -sets can you choose inside a set of size
-sets can you choose inside a set of size  if there is no sunflower with
if there is no sunflower with  petals and a head of size less than
petals and a head of size less than  ? The maximum number is (unless I’m out by 1 in one of the parameters) the number
? The maximum number is (unless I’m out by 1 in one of the parameters) the number  .
.
Suppose we had a complete understanding of that question. How would it feed back into the original conjecture? A trivial observation, implicit in what you write, is that for fixed with
with  ,
,  tends to infinity with
tends to infinity with  . That is because we can take all sets that contain some fixed set of size
. That is because we can take all sets that contain some fixed set of size  , which of course is why you suggest a bound of the form
, which of course is why you suggest a bound of the form  .
.
It looks to me as though what one would want is some kind of "inverse statement", which would say that if you have a system with lots of sets but no sunflower with petals and a head of size less than
petals and a head of size less than  , then in some sense the example must look a bit like the simple one of all sets containing a given
, then in some sense the example must look a bit like the simple one of all sets containing a given  -set, which then makes it much easier to find a sunflower, because there will be some set with a large link, which makes an inductive argument reasonably efficient. But maybe I am missing something: if one could get the right bound for
-set, which then makes it much easier to find a sunflower, because there will be some set with a large link, which makes an inductive argument reasonably efficient. But maybe I am missing something: if one could get the right bound for  to within a constant without saying anything about systems that get close to the bound, is that enough to solve the original conjecture?
to within a constant without saying anything about systems that get close to the bound, is that enough to solve the original conjecture?
Dear Tim, I think that Erdos-Ko-Rado theory is largely the quest of inverse theorems of this kind, and sometimes they hold on the noise if n is large with respect to k. What makes it easier for us is that we dont want to understand matters on the nose, but what makes it harder is that the crucial regime would be when n is not very large compared to the other parameters (but more than linear in k, of course).
Here’s another question that might be interesting. Suppose we decide that we would like to find a sunflower with a head of size less than . Of course, there is no guarantee that we will succeed. But we would like to be able to say something strong if we fail. One simple thing we could ask is the following. (No doubt it has been asked many times by people who have thought about the problem — indeed, perhaps this is how the best known bounds are proved — but I am not familiar with the literature.) What is the smallest number
. Of course, there is no guarantee that we will succeed. But we would like to be able to say something strong if we fail. One simple thing we could ask is the following. (No doubt it has been asked many times by people who have thought about the problem — indeed, perhaps this is how the best known bounds are proved — but I am not familiar with the literature.) What is the smallest number  of sets needed to guarantee that there is either a sunflower with
of sets needed to guarantee that there is either a sunflower with  petals and a head of size less than
petals and a head of size less than  or a set of size
or a set of size  that is contained in at least
that is contained in at least  of the sets? The case
of the sets? The case 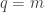 is an obvious one to look at, but
is an obvious one to look at, but 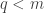 could be interesting too.
could be interesting too.
two little things: We run a “polymath” seminar here in Jerusalem, and I will try to summarize ideas we come up with here. I will also help Gil “run” this polymath to some extent, whatever that implies (I do not know what I have gotten myself into)
second, the first of some possible approaches, based on Stanley–Reisner theory: The sunflower problems are questions about 0-th Betti numbers in simplicial complexes generated by cardinality k simplices, and links of subsets. I would propose that it might be simpler to make statements about total Betti numbers first, i.e. (perhaps weighted) sums of Betti numbers of the complex and its links, over all subcomplexes induced by facets (=maximal simplices=k-sets).
To see the merit this approach might have is to notice that if we sum over the subcomplexes induced by vertexsets, then it is possible to relate such sums to problems in commutative algebra, which should be more attackable.
Now, we are dealing with a “dual” problem that emphasizes the role of the maximal simplices.
One could try to dualize the complex; this is a little tricky and usually works best if the complex is close to being Cohen–Macaulay (i.e. the homology is concentrated in the top dimension in every link). We might be able to use this to our advantage, however: If the Betti numbers of the total complex are large already, we are fine. If not, the complex is “close” to acyclicity, we modify the complex by killing some few homology generators and dualize to use algebraic approaches.
Note that Stanley–Reisner rings are just models for intersection theory; this is therefore also related to analytic approaches (like Fourier-analytic methods) on simplicial complexes.
Dear Karim, this is indeed a nice but perhaps very drastic strengthening of the conditions. We can start by asking the analogue of Erdos-Ko-Rado: : How large can a collection of k sets from {1,2,…,n} so that the simplicial complex spanned by every subset of them has total betti number less than 2 (or r)? all sets containing one element is an example. (Or one element from a set of size r-1 for general r.) Possibly this is best possible without any restriction on n.
I made no change to the conditions. Also, while your example has small Betti numbers, the link does not. Summing over Betti numbers might be more stable under algebraic shiftings
A small remark: it seems that it is assumed that families are without redundancy (otherwise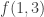 would be 4 while the given upper bound is 2), but I guess it makes little difference.
would be 4 while the given upper bound is 2), but I guess it makes little difference.
I wonder what are the known lower bounds and the example realizing them? Is there any insight to gain looking at them?
Dear Benoît, For r=3 the best lower bound is roughly . You get easily
. You get easily 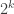 by considering all k-sets from {1,2,…,2k} not containing both j and k+j. See also this mathoverflow problem http://mathoverflow.net/questions/163689/what-is-the-best-lower-bound-for-3-sunflowers
by considering all k-sets from {1,2,…,2k} not containing both j and k+j. See also this mathoverflow problem http://mathoverflow.net/questions/163689/what-is-the-best-lower-bound-for-3-sunflowers
I whipped up a quick wiki page for this project at http://michaelnielsen.org/polymath1/index.php?title=The_Erdos-Rado_sunflower_lemma
Of course it could do with many further additions (e.g. to the bibliography).
Some typos in the post: in the statement of the Erdos-Rado theorem, “syatem” should be “system”, A few paragraphs afterwards, “iswill” should be “will”. After Question 2, “Eado” should be “Rado”.
⭐ ❗ 💡 great choice of problem. sunflowers show up in complexity theory lower bounds (razborovs nevinlinna prize winning research, reformulated, see also lower bounds on monotone circuits by Rossman) and am interested in that angle. would like to suggest that this problem can be attacked (to some degree) empircally by writing code to find sunflowers for small “sizes” and look at trends in that area. the questionable area is whether it would take too much CPU to look at even “small” sunflowers and that maybe trends for “small” sunflowers dont hold for larger ones, but these are all (pessimistic) assumptions.
heres a question that showed up on cstheory SE The state of art for sunflower system.
plz comment on my blog (click on name icon) or drop by cstheory salon chat if anyone would like to pursue this further.
Dear Vzn, right the Delta system theorem is useful in some proofs for lower bounds and also it is quite useful in extremal combinatorics. I dont think the conjecture will make a difference for the TCS applications.
One thing that could perhaps be crowdsourced fairly easily is to collect upper and lower bounds on f(k,r) for small values of k and r (as was done in Polymath1). It may be that the structure of the extremising examples may give some clues. Presumably there are already some results in these directions?
Dear Terry, many thanks for setting the wiki! (typos fixed).
At some points it will be useful to get a feeling for the ideas involved in the current upper and lower bounds.
I think there is some information in the literature on small value of k and r. There is some product technique available for lower bounds and some very small example with 10 sets of size 3 accounts for the best known lower bounds.
It will be useful to think about the balanced (aka multipartite; colored) case. Namely when you can color the ground set by k colors and every set in the family contains exactly one element from every color. There the best example known for r=3 is of size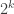 and for general value of r,
and for general value of r,  . (Just take k color clases with r-1 elements in each.) I am not aware of a better lower bound for the balanced case.
. (Just take k color clases with r-1 elements in each.) I am not aware of a better lower bound for the balanced case.
Naive question: if we look only at intersecting collections of k-subsets (i.e. we impose a condition much stronger than “no headless sunflowers,” do we have stronger bounds on how large this collection must be before it contains a 3-sunflower?
I’m not sure I quite understand your question here. If we know, for example, that there is some element that belongs to all the sets, then the problem reduces from estimating f(k,r) to estimating f(k-1,r). That is of course a stronger bound, so perhaps that is indeed what you are getting at. Would the following be a reasonable attempt at a more precise version of your question: is it the case that if you insist that your family of sets is an intersecting family, then you can’t do much better than f(k-1,r)?
Hmm, that seems rather interesting, so perhaps I do understand your question after all …
Dear Jordan, As far as I remember (but very vaguely) looking at intersecting collections is indeed a trick to get some improvement on the original upper bound (for all collections). (I don’t remember the details and the reason it worked was mysterious.) Now I usually (and also in the post above) use the term “intersecting family” for the case that every two sets have an element in common. I dont remember how it is used to improve the upper bound. But I will try to ask.
Can we do better by demanding minimum sizes on the intersections in the intersecting collections?
For example, any 3-sunflower-free collection of k-sets where each pairwise intersection has minimum size (k-1) must have at most (k+1) elements.
Any 3-sunflower-free collection of k-sets where each pairwise intersection has minimum size (k-2) must have at most 5/8 k^2 + O(k) elements. [It may be possible to do considerably better than this bound, I’m not certain.]
Working our way downwards will only get us to intersections of k-sets of size ~2k/3, unless we come up with some more clever arguments — but we could look for such arguments.
Dear Craig, This is a nice idea but I am not aware that it is helpful.
This has certainly been asked before (for example in the comments of my mathoverflow question linked to above). I could not find anything non-trivial about this version. Note that the “easy” bound is improved to $k!$ in this version by the same proof that you can find e.g. here: https://gilkalai.wordpress.com/2008/09/28/extremal-combinatorics-iii-some-basic-theorems/.
is improved to $k!$ in this version by the same proof that you can find e.g. here: https://gilkalai.wordpress.com/2008/09/28/extremal-combinatorics-iii-some-basic-theorems/.
Dear Pálvölgyi, I dont think you get k! because the property of being intersecting is not preserved when you move to links. Also an upper bound k! for the intersecting case gives you an upper (k+1)! for the general case since for any collection without delta system of size r you get an intersecting family by adding a new element to your ground set and then adding it to all the sets.
This last “cheap” argument of moving to intersecting families suggests it might be not be useful at all. But surprisingly it is useful to think about the problem for intersecting families and this allow to improve for r=3, the bound to
bound to  . (Noga Alon observed this argument as a student and it was observed earlier too, perhaps by Abbot.)
. (Noga Alon observed this argument as a student and it was observed earlier too, perhaps by Abbot.)
The simple argument for the case when every pair intersects: Let f(k) be the maximum number of k-sets in a family with no 3-delta system in which every two sets intersect. Then f(2)=3. For k>2 fix a set A of the family and classify all others according to their intersection with A, note that for every B, C with the same intersection with A, B-A and C-A intersect, as otherwise A,B,C form a delta system. This gives
giving something like what’s above
Indeed and thanks for the improved argument. ps. My first name is Dömötör.
GK: oops sorry, I think I knew that, and also that in Hungarian one puts the last name first; but in difficult decisions, especially after careful thinking, I often make the Z/2Z-mistake, namely of choosing the wrong alternative.
I would like to advertise a (somewhat) well-known special case of the sunflower conjecture, in case some people don’t know it.
Let be an abelian group, where a good example is
be an abelian group, where a good example is  . Let
. Let  . The question is: what is the minimal
. The question is: what is the minimal  that guarantees
that guarantees 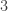 disjoint subsets of the elements, each having the same sum. The conjecture is
disjoint subsets of the elements, each having the same sum. The conjecture is 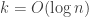 . If it is false, then Coppersmith and Winograd showed that one can multiply two
. If it is false, then Coppersmith and Winograd showed that one can multiply two 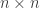 matrices in essentially quadratic time. If true, this would be a huge algorithmic breakthrough.
matrices in essentially quadratic time. If true, this would be a huge algorithmic breakthrough.
This question is indeed a special case of the sunflower conjecture, as was observed by Alon, Shpilka and Umans. For any potential sum let
let ![F=\{S\subseteq [k]:\sum_{i\in S}g_i=s\}](https://s0.wp.com/latex.php?latex=F%3D%5C%7BS%5Csubseteq+%5Bk%5D%3A%5Csum_%7Bi%5Cin+S%7Dg_i%3Ds%5C%7D&bg=ffffff&fg=333333&s=0&c=20201002) . The most popular sum has
. The most popular sum has  . If the sunflower conjecture is true, then for a large enough
. If the sunflower conjecture is true, then for a large enough 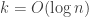 we will have that
we will have that  contains a
contains a 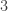 -sunflower; its petals form the
-sunflower; its petals form the
required disjoint subsets.
The Erdos-Rado bound gives that is sufficient. With some optimization, this can be slightly improved to
is sufficient. With some optimization, this can be slightly improved to 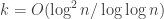 . As far as I know, nothing better is known.
. As far as I know, nothing better is known.
That’s very interesting! How do you do the optimization to get the extra log log?.
Let . There are
. There are 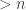 subsets of size
subsets of size  , hence there must be two with the same sum. Removing common elements, we get two disjoint subsets, lets call them
, hence there must be two with the same sum. Removing common elements, we get two disjoint subsets, lets call them 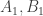 . We can remove them and repeat this process
. We can remove them and repeat this process  times to obtain disjoint subsets
times to obtain disjoint subsets  with
with  with the same sum. Now there must be two disjoint subsets of
with the same sum. Now there must be two disjoint subsets of  with the same sum, say
with the same sum, say 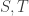 . Then the following 4 subsets have the same sum:
. Then the following 4 subsets have the same sum:  .
.
In a 2005 paper (I do not know how to link it) H. Cohn, R. Kleinberg, B. Szegedy and C. Umans formulate a group theoretic conjecture that also leads to esentially quadratic matrix multiplication. A natural question would be whether these conjectures are equivalent.
I agree. I think that in general that type of group theoretic conjectures are of the “Ramsey-type” variety, similar in spirit to the sunflower conjecture; understanding this connection explicitly can be very valuable. Unfortunately, they never made the full version publicly available, so many details remain vague…
I was thinking whether some topology can help to find three disjoint equivoluminous subsets. The only theorem I know that does such things is the Z3-version of Borsuk-Ulam and its simplest form is the Zp-Tucker lemma. I’m sure that there are people here who know this much better, but let me try to formulate a version that I hope to be true and hopefully someone can prove it (though most probably it won’t be…)
Let F be a map from the ordered triples (A,B,C), where these are not-all-empty three disjoint subsets of Zn, to some appropriately chosen small finite group G, that I would like to have an element w, that behaves like the third root of unity; if we combine it with F, then F(A,B,C)=wF(A,B,C). Then the conclusion of the lemma would be (if G is small enough) that there are A<D, B<E, C<F such that F(A,B,C)=F(D,E,F). Now to apply the lemma to our case, we could choose . Then the conclusion gives that
. Then the conclusion gives that  , and if w really behaves like the third root of unity, then this would imply that we have three disjoint equivoluminous subsets.
, and if w really behaves like the third root of unity, then this would imply that we have three disjoint equivoluminous subsets.
That’s very interesting. I suppose also Tverberg’s theorem come to mind. These kind of questions came up (even partially motivated) some old work by Alon, Friedland and me. We considered . One problem that came up (in analogy to Tverberg’s theorem) was: how many vectors guarantee three (non empty) disjoint subsets whose sums are the same. A weaker statement that we observed and found various applications was that
. One problem that came up (in analogy to Tverberg’s theorem) was: how many vectors guarantee three (non empty) disjoint subsets whose sums are the same. A weaker statement that we observed and found various applications was that 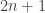 elements guarantee a non empty subset that sum up to zero. (This is weaker since you can take the union of the three sets.) Our result gives that a graph with n vertices and 2n+1 edges contains a non empty subgraph all whose degreed are divisible by 3, and, in particular, if all degress are at most five it contains a 3-regular subgraph. The stronger question will give three edge disjoint subgraphs so that the degree of every vertex modulo 3 is the same for all three. For degrees at most five (if applies) the conclusion will give 3-regular subgraph of type I (3-edge colorable.)
elements guarantee a non empty subset that sum up to zero. (This is weaker since you can take the union of the three sets.) Our result gives that a graph with n vertices and 2n+1 edges contains a non empty subgraph all whose degreed are divisible by 3, and, in particular, if all degress are at most five it contains a 3-regular subgraph. The stronger question will give three edge disjoint subgraphs so that the degree of every vertex modulo 3 is the same for all three. For degrees at most five (if applies) the conclusion will give 3-regular subgraph of type I (3-edge colorable.)
Funnily enough, when Shachar, Omid, Kaveh and I were working on this, we briefly discussed the prospects for a topological argument, but didn’t manage to find one. I do think it is a very interesting direction though.
Actually it is interesting to compare what various statement would give for graphs and hypergraphs. Say you have a hypergraph on n vertices with e edges. If e>2n then by a polynomial argument (essentially Warning-Chevallay) you get a nonempty subhypergraph with all vertices have degree divisible by 3. From Tverberg’s theorem you can find in the hypergraph three edge-disjoint parts with the same support (namely a vertex belongs to an edge in one iff it belongs to an edge in all three.) The question about three sets with the same sum modulo three is equivalent to a Tverberg like partition with the additional property that the degrees modulo 3 are the same in the three parts. (So its a common strengthening)
You can ask similar things for incidences between k sets and k-1 sets.
If you have a k-uniform hypergraph with more than edges
edges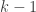 in 0(mod 3) edges. You can also find (**) (Tverberg) three edge disjoint subhypergraphs so that every set of size $latex(k-1)$ either belong to an edge in all three or in none. Again I dont know how many edges guarantee (***) three parts with the same degree modulo 3. Both these conditions imple a subhypergraph so that (****) every set of k-1 edges belong to non or at least three edges. For (****) the precise necessary number of edges is slightly less
in 0(mod 3) edges. You can also find (**) (Tverberg) three edge disjoint subhypergraphs so that every set of size $latex(k-1)$ either belong to an edge in all three or in none. Again I dont know how many edges guarantee (***) three parts with the same degree modulo 3. Both these conditions imple a subhypergraph so that (****) every set of k-1 edges belong to non or at least three edges. For (****) the precise necessary number of edges is slightly less  .
.
you can find (Chevallay) (*) a nonempty sub-hypergraph with every set of size
This requires the type of homological arguments I talk about (or something equivalent).
Anyway vaguely speaking Tverberg’s theorem seems also relevant.
If A,B,C are subsets of where
where  , it seems that Borsuk-Ulam type arguments only work when the group G (as described above) has size
, it seems that Borsuk-Ulam type arguments only work when the group G (as described above) has size  . However, for the three disjoint equivoluminous subset problem, we need G which is exponentially larger. So: can we hope for Borsuk-Ulam type arguments to work in such a regime?
. However, for the three disjoint equivoluminous subset problem, we need G which is exponentially larger. So: can we hope for Borsuk-Ulam type arguments to work in such a regime?
By the way, let me introduce a weaker variant which might be easier (I don’t know of any improved bounds for it, though). If . What is the minimal size of S that guarantees the existence of two disjoint subsets A,B of it such that
. What is the minimal size of S that guarantees the existence of two disjoint subsets A,B of it such that  ?
?
Indeed it seems that we would need , not sure how one could overcome this.
, not sure how one could overcome this.
About sum(A)=2sum(B), I think there is a chance that this problem is just as hard as the original; in the necklace splitting problem there is no other proof for the 1:2 ratio with two thieves than using the proof for 3 thieves.
I don’t know if this helps in any way, but since Gil mentioned his result on 3-regular subgraphs, I would like to mention this: vectors in
vectors in 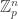 , then it can be shown that there are at least
, then it can be shown that there are at least  distinct subsets of these vectors that sum up to zero. This follows from something known as Warning’s Second Theorem with Resricted Variables, http://arxiv.org/abs/1404.7793. For our case, we have
distinct subsets of these vectors that sum up to zero. This follows from something known as Warning’s Second Theorem with Resricted Variables, http://arxiv.org/abs/1404.7793. For our case, we have  non-empty subsets that sum up to
non-empty subsets that sum up to  , where
, where  is the given number of vectors in
is the given number of vectors in  .
.
if you are given
Dear Anurag, This is very interesting. As the proof of Chevallay-Warning theorem is very useful in various combinatorial contexts I wonder if the methods og Warning second theorem can also be useful.
Dear Gil,
Indeed, this generalization of Warning’s second theorem is useful in other combinatorial contexts. Clark-Forrow-Schmitt have discussed some applications to davenport constants, EGZ type theorems, set systems with no union of cardinality 0 modulo m, in their paper. Later on, Pete Clark generalized this further and mentioned some more applications, including your subgraph result with Alon and Friedland, in “Fattening up Warning’s Second Theorem” (http://arxiv.org/abs/1506.06743). Of course, there might be many more applications. The basic principle here is that the existence of combinatorial objects corresponding to common zeros of a system of polynomials can sometimes be converted to explicit lower bounds on the number of objects that exist.
On a related note, the 1993 result of Alon and Furedi that Clark-Forrow-Schmitt use to prove their restricted variable generalization of Warning’s theorem has even more combinatorial applications of its own (Reed-Muller type codes, Schwartz-Zippel lemma, Blocking Sets, Partial Covers, etc.) as is discussed my work with Clark, Potukuchi and Schmitt: “On Zeros of a Polynomial in a Finite Grid” (http://arxiv.org/abs/1508.06020).
For the balanced case there is such a nice looking conjecture, , so this version has the most chance to have some simple proof. Take the r=3 case and denote the color classes by
, so this version has the most chance to have some simple proof. Take the r=3 case and denote the color classes by  for some hypergraph
for some hypergraph 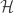 . We can try an inductive proof by getting rid of
. We can try an inductive proof by getting rid of 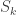 . So denote the (k-1)-uniform hypergraph that is the restriction of
. So denote the (k-1)-uniform hypergraph that is the restriction of 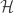 to
to  by
by  . It is possible that we get some edges twice, but not thrice, as that would mean a sunflower. So if
. It is possible that we get some edges twice, but not thrice, as that would mean a sunflower. So if 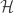 had more than
had more than 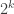 edges, then
edges, then  has more than
has more than  edges, and thus contains a 3-sunflower by induction. Denote these three sets by A, B, C. If at least two of A, B and C have two extension to an edge of
edges, and thus contains a 3-sunflower by induction. Denote these three sets by A, B, C. If at least two of A, B and C have two extension to an edge of 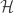 , then a simple case analysis shows that we also have a 3-sunflower in
, then a simple case analysis shows that we also have a 3-sunflower in 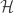 . If at most two of A, B and C have two extension to an edge of
. If at most two of A, B and C have two extension to an edge of 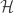 , then we can deduce that
, then we can deduce that  has more than
has more than 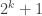 edges and maybe use this somehow, possibly with a stronger induction hypothesis.
edges and maybe use this somehow, possibly with a stronger induction hypothesis.
Dear Dömötör, right, this is a very appealing conjecture (but maybe it is already known to be false)
Hyperoptimistic conjecture (r=3): The maximum size of a balanced collection of k-sets without a sunflower of size 3 is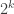 .
.
Hyperoptimistic conjecture (general case): The maximum size of a balanced collection of k-sets without a sunflower of size r is .
.
A collection of k-sets is balanced (aka multipartite; colorful) if we can divide the ground set to k parts so that every set in the collection contain one element from each part.
(We did have some hyperoptimistic conjectures (still open) in polymath1 and perhaps a few others. Also balanced collections of sets and monomials played special role in polymath3.)
For the balanced case, let’s try this example: consider k=3 and let |V_1|=|V_2|=|V_3|=3, a 3-set is denoted by ijk if we take the i-th element from V_1, j-th element from V_2 and k-th element from V_3. For example, the 2^k construction can be regarded as the family of all the binary sequences of length k.
Now we can look at the following 9 3-sets:
000, 001, 010, 011, 100, 101, 112, 122, 212
I briefly checked this and I believe there is no sunflower of size 3, while it gives 9>8 subsets. Maybe there is a way to generalize it, I will think more about it and report back.
Yeah, Hao’s construction seems correct, then so much about the hyperoptimistic conjecture…
Hao, what happens if you add any other 3-set to your system? Do you get sunflowers?
Just to check, should that last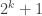 be
be  ?
?
Yeah, thx. Wish there was a way to edit, like on mathoverflow.
GK: I will try to edit the math on a routine basis, and will edit if asked other things.
I agree, but at least with WordPress the owner of the blog can edit comments, which is useful with Polymath projects (especially when the maths doesn’t compile properly).
I’d like to pursue Jordan’s thought a little bit — or what I take to be his thought. For simplicity I’ll look at the case k=3.
Given a set system, it is natural to ask whether we can somehow gain by deciding in advance what we think the size of the head of the sunflower should be. That is, we try to identify some parameter of the system that measures in what way it is “spread out” or “concentrated” and then use the value of that parameter to get a better bound when we are searching for a sunflower with a head of a particular size.
For example, suppose we cannot find r disjoint sets in the collection. In the simple proof we take the union of a maximal disjoint family and use nothing more than the fact that every other set intersects it. But a family of sets of size 3 that contains no r disjoint sets has much stronger properties than merely containing one maximal disjoint subfamily of size less than r, so we are throwing away a lot of information here. What can be said about such families? Can we prove some kind of lemma with a regularity flavour that would allow us to conclude that every family of 3-sets either contains r disjoint sets or a subfamily that is “well intersecting” in some sense to be formulated? (I think the best thing to aim for would be a property that is significantly weaker than saying that any two sets intersect, but strong enough to improve bounds in proofs.)
Let me call such a family 1-rich. (I don’t know what 1-rich means, but it is something like that we now guarantee that pairs of sets that intersect in at least one element “appear almost everywhere”.) Now we would like to argue that inside a 1-rich family, either we can find a sunflower with a head of size 1 and r petals, or we can find a subfamily that is 2-rich, and so on. And the hope would be to get better bounds this way.
Again, there is a high probability that these remarks are either (i) nonsense or (ii) a standard approach that has been used to prove some of the existing improvements to the easy bound.
It is probably not what we want, but still I’m curious to know what is known about the following Ramsey-type question. Suppose you have a collection of sets of size 3 and you would like to find either a subfamily of size r consisting of disjoint sets or an intersecting subfamily of size m. How many sets do you need?
When I say Ramsey-type question, it is of course precisely a Ramsey question where you colour pairs of sets according to whether they intersect or not. The hope would be that because the sets have size 3, the complexity of the resulting graph cannot be too great, and therefore the bounds one obtains should be much better than for a general graph.
The simple argument gives a bound that could be regarded as what one would like to beat. If there are no r disjoint sets, then there is a set of size at most 3(r-1) that intersects all the sets in the system, so there is an intersecting family of size at least n/3(r-1), so we get an upper bound of 3(r-1)m.
One can also get a lower bound of (r-1)(m-1) just by taking r-1 disjoint intersecting families of size m-1. So it looks as though this Ramseyish question is not helpful.
And I realize now that I didn’t mean to ask it this way. I meant to take r=3 not k=3.
So here’s what I should have asked. Suppose you have a family of sets of size k and you would like either three disjoint sets or an intersecting subfamily of size m. How many sets do you need? The simple argument gives a bound proportional to mk. Can one do better? Can one do as well as 100m? (I haven’t thought about this, so there is probably a very simple counterexample to that last hyperoptimistic conjecture.)
A very small remark is that when k=2 one can improve on the trivial argument by a factor of 2. The trivial argument I have in mind is that we pick a maximal disjoint collection of sets and take its union, and then use pigeonhole to get a family of sets that intersect in one point. That gives a bound of 4m or so. But if we have two disjoint sets A and B in the collection, then we can argue as follows. The sets disjoint from A form an intersecting family (since if two of them are disjoint then together with A we get three disjoint sets) and the sets disjoint from B form an intersecting family. But there are at most 4 sets that intersect both A and B, so the total number of sets needed to guarantee an intersecting family is at most 2m+5. (That’s the sets A and B and then 2m+3 more sets, at least 2m-1 of which are disjoint from at least one of A and B, after which pigeonhole gives us an intersecting family of size m.)
This is extremely weak evidence that maybe one can do quite a bit better than mk in general.
Is decomposing the family to subfamilies depending on what they intersect the union of maximal independent sets useful?
For example, the case and $m$ large enough: Suppose that
and $m$ large enough: Suppose that  is a family of 3-sets without three independent sets and without an intersecting subfamily of size
is a family of 3-sets without three independent sets and without an intersecting subfamily of size  .
.
Let be the union of two disjoint sets in
be the union of two disjoint sets in  . For
. For 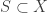 , let
, let  . Suppose that
. Suppose that  .
.
Noticing that the sets disjoint from form an intersecting family and the sets disjoint from
form an intersecting family and the sets disjoint from  form an intersecting family, we have
form an intersecting family, we have  .
.
Also, if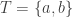 is the set achieving
is the set achieving  , then
, then  ,
,  , and
, and  is intersecting. This implies that
is intersecting. This implies that  .
.
If the above works, then we should have an upper bound of , a bit better than the simple pigeonhole bound of
, a bit better than the simple pigeonhole bound of 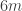 .
.
Here are some suggestions regarding shifting (aka compression).
A collection F of k-subsets from [n]={1,2,…,n} is shifted (or compressed) if whenever a set S is in the collection and R is obtained by S by lowering the value of an element, then R is also in the family.
A shifting process is a method to move from an arbitrary family to a shifted one with the same cardinality.
Let me make a notation: P(r,m) is the following property of families of k-sets: Not having a sunflower with r petals and head of size at most m-1. Our aim is to find upper bounds for families of k-subsets of {1,2,…,n} with property P(r,m). We also write P(r) for P(r,k-1) which is the property of containing no sunflower of size r at all.
A very basic facts from Erdos-Ko-Rado theory is that P(2,m) and P(r,1) are preserved under shifting. But not having a sunflower is not preserved under shifting. (As far as I remember the problem for shifted families is easy.)
It is still possible that not having a sunflower for the family is translated to a weaker statement for the family obtained from it by shifting.
Conjecture: If F is a family of k-subsets of {1,2,…,n} with property P(r,m) then for the shifting of F, every set has at least m elements in the set {1,2,…,m+(r-1)k}.
Perhaps the first case to consider is:
Question: What can be said for shifting families with property P(3,2).
The conjecture is that every set in the shifted family will at least two elements from {1,2,…,2k+2}
We can also ask similar questions for balanced families. Here we need to define what do we mean by a shifted family, and what balanced shifting process we use. (We can also apply ordinary shifting that will destroy balanceness). In view of the hyperoptimistic conjecture, and the fact that the example will be shifted under every reasonable definition, it may be possible that for balanced complexes the property P(r,m) is simply preserved under shifting.
Conjecture (version of the hyperoptimistic conjecture): For balanced complexes the property P(r,m) is simply preserved under balanced shifting.
I will try to justify a weaker conjecture that still suffices for the delta system conjecture.
Conjecture: ordinary shifting of balanced families with property P(r,m) leads to a shifted family so that every set has at least m elements {1,2,…,(r-1)k}.
Question: What can be said about shifting (or some sort of balanced shifting) for balanced families with the property P(3,2)?
GK: Edited, Nov 5. Completely off topic: There is a startling announcements that if verified will represent off-scale scientific breakthrough. Laci Babai announced a quasipolynomial algorithm for graph isomorphisms, see here, here and here. Lipton and Regan blog discusses this breakthrough and bring a remarkable 2013 paper by Babai and John Wilmes with a quasi polynomial time algorithm for Steiner systems isomorphism.
Competing terms: We have a few competing terms for the same notion delta systems or sunflowers, shifted or compressed? and a couple others. A poll is called upon (choose among the competing terms)
About “head” and “capitulum”::
wikipedia calls it the “kernel”:
https://en.wikipedia.org/wiki/Sunflower_%28mathematics%29
Stasys Jukna’s book, Extermal Combinatorics,
http://www.thi.informatik.uni-frankfurt.de/~jukna/EC_Book_2nd/draft.pdf
which has a very nice chapter on the sun flower lemma, calls it the “core”.
Dear Christian, thanks for the comment. We had clear choices of “sunflower” “shifting”, “head”, and “r pairwise disjoint sets”. (But we neither offered core or kernel). Let’s also stay with “balance”. By now I think we can use more than one competing term with no confusion.
I don’t think that shifting on sunflower-free balanced sets remains such, if I understand correctly the suggestion. Consider the following example with k=2,r=3 and color sets {1,2,3} and {4,5,6}: {{2,4},{2,5},{3,6}}. It does not contain a 3-sunflower but if we shift the elements in the 1st color set we get {{1,4},{1,5},{1,6}} which is a sunflower.
Thanks Gil for this initiative!
Just a small remark: (1) implies (2) (typo: r instead of 3 in (2) GK:corrected ) in Gil’s:
(1) Conjecture (version of the hyperoptimistic conjecture): For balanced complexes the property P(r,m) is simply preserved under balanced shifting.
(2) Hyperoptimistic conjecture (general case): The maximum size of a balanced collection of k-sets without a sunflower of size r is (r-1)^k.
Indeed, if |F|>(r-1)^k then there is a color i and k-set S where the vertex in S with color i is not of the least r-1 vertices of color i. So F has a sunflower with head having the minimal vertex of any color different from i, and each of the r petals (size 1 each) have a different vertex of the minimal r vertices of color i.
Of course (1) can be tested on examples, also by computer, and we plan to try some tests soon.
Hi Gil, thanks for the project. I’ve been trying to follow some threads here.
How does that P(2,m) and P(r,1) are preserved under shifting follow Erdos-Ko-Rado theory? I must be missing something here.
Dear Shen-Fu, one of the basic facts about shifting families of sets is that the following properties are preserved:
1) The family is intersecting (every two sets in the family have nonempty intersection)
2) Every two sets in the family has at least m elements in common
3) from every m sets in the family at least two ihave nonempty intersection.
(This is mentioned in this post https://gilkalai.wordpress.com/2008/10/06/extremal-combinatorics-iv-shifting/ and the reduction to shifted families is crucial for the extremal results for families satidfying these properties.)
This is also true for (exterior) algebraic shifting (See http://www.ma.huji.ac.il/~kalai/japan.pdf .)
What I meant by “follow Erdos-Ko-Rado theory” is more precisely “proved as part of the study of Erdos-Ko-Rado type theorems”.
I see. Thanks for the clarification. Yes it is not hard to deduct these from definition.
To summarize the comments in my mono-thread above, there are a few related questions for which I would be interested to know what is known.
1. How large a family of k-sets do you need before either three of them are disjoint or m of them form an intersecting family?
2. How does the answer to 1 change if you ask not just for a pairwise intersecting family but for a family of sets with nonempty intersection?
3. How does the answer to 1 change if you add the assumption that no two of the sets intersect in more than one element?
Here’s a fanciful idea. Recall first that if you have a whole lot of dense subsets of a finite set, then the method of dependent random selection can be used to select a large fraction of them so that almost all intersections have approximately the same size. (The rough idea is that you choose a few elements at random and then choose all the sets that contain those elements. This makes it much more likely that you will choose a given pair of sets if they have a large intersection, so you can end up with nearly all pairs of sets intersecting in the “essentially largest” possible amount.)
Suppose we could find some clever method of doing something similar for a collection of sets of size k. Suppose, for instance, that we could ensure, after passing to a reasonably large subfamily, that all pairs intersect in exactly j. Then for r=3 we could reason as follows. As usual, let A and B be a maximal disjoint family. (If we can’t find two disjoint sets, then the argument is similar but easier.) By pigeonhole, WLOG at least half the other sets intersect A. Since they must intersect in a set of size , by pigeonhole again, a fraction at least
, by pigeonhole again, a fraction at least 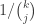 of those intersections must be the same, and we get a sunflower because if all intersections have size
of those intersections must be the same, and we get a sunflower because if all intersections have size  then there can be no further intersection outside A. The fraction we’ve dropped down to is now only exponential because
then there can be no further intersection outside A. The fraction we’ve dropped down to is now only exponential because 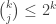 .
.
More generally, it seems that if we can ensure some degree of uniformity in the sizes of the intersections, it should be a big help. So maybe it would be interesting to ask a general question about -uniform hypergraphs: are there ways of passing to subfamilies where the sizes of the intersections become much more uniform?
-uniform hypergraphs: are there ways of passing to subfamilies where the sizes of the intersections become much more uniform?
One way one could try to do this is via Gil’s “many differential operators” idea; essentially, the support of a k-1-cycle with respect to m differential operators has to have degree at least m+1 in the (k-1)-subsets. On the other hand, any set that is not in any such cycle must be connected in degrees < m+1.
Let me expand on this since Tim’s proposal is rather nice: there is a slight downside to the approach via boundary (not differential, sorry) operators: Lets say we take C the subcomplex of those k-sets supported in some (k-1)-cycle, then we only get a lower bound (of m+1) on the average degree of (k-1)-sets in C (and not an upper bound).
At the same time, about the complement D of C we cannot say much except that in some (k-1)-set of each k-set, the degree is smaller than m+1, and not much about the other degrees. However, one could then pass to links and try to iterate.
I can’t work out what, from Gil’s contributions above, is what you are referring to when you talk about his “many differential operators” idea. Could you give me a pointer?
Sorry — I was in the middle of writing my comment when you posted yours.
This is a very nice idea and so is the Ramsey flavour one from the previous one. Families of sets (from an n element set) with all pairwise intersections of the same size are very sparse they can have at most n elements and also if you allow only s different intersection sizes, you can have at most sets and there are various results (a few make crucial usage on the delta system theorem) which gives even stronger upper bounds in terms of the allowed intersection sizes. So for this plan to work it needs to be quite delicate. Maybe “approximately the same size” and the later “exactly j” in the plan above should be thought of as a condition that the intersection sizes are distributed similar to that of a random collection of some sort. Actually I dont know what the dependent random selection method actually gives. It could be useful to elaborate on that. Anyway, since the “every pairwise intersection is of size j” is so unrealistic I find it difficult to see how the conclusion from it extends. But maybe the same conclusion can be derived from something much weaker.
sets and there are various results (a few make crucial usage on the delta system theorem) which gives even stronger upper bounds in terms of the allowed intersection sizes. So for this plan to work it needs to be quite delicate. Maybe “approximately the same size” and the later “exactly j” in the plan above should be thought of as a condition that the intersection sizes are distributed similar to that of a random collection of some sort. Actually I dont know what the dependent random selection method actually gives. It could be useful to elaborate on that. Anyway, since the “every pairwise intersection is of size j” is so unrealistic I find it difficult to see how the conclusion from it extends. But maybe the same conclusion can be derived from something much weaker.
What Karim referred to is an algebraic rather than probabilistic method to obtain a subfamily which may behave nice in terms of distribution of intersections. I don’t see precisely how this may work and we did not discuss yet many differential/boundary operators. But we can keep it in mind.
I will explain the “many boundary operators” machinery in the next post.
Can you give a reference (to finding a “large fraction” such that every intersection is of approximately the same size).
Tim Gowers, Omid Hatami, Kaave Hosseini and myself thought a while back on the problem I mentioned earlier, of finding three disjoint subsets with equal sums. We didn’t make much progress, but we had a few observations that might be useful.
Let and
and 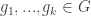 . The goal of finding 3 disjoint subsets with equal sums can be equivalently phrased as follows: find a nontrivial solution to
. The goal of finding 3 disjoint subsets with equal sums can be equivalently phrased as follows: find a nontrivial solution to 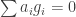 where
where 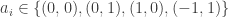 .
.
Note that the easy problem of finding 2 disjoint subsets with equal sum (which holds whenever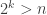 by pigeonhole) corresponds in the notation above to
by pigeonhole) corresponds in the notation above to  .
.
So, here is an intermediate question: what is the smallest k for which there is a nontrivial solution with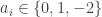 . I don’t know of any better bounds for this problem than for the full problem.
. I don’t know of any better bounds for this problem than for the full problem.
Regarding the line of thought about shifting: The boldest conjecture would be that the P(r,m) condition is preserved under balanced shifting for balanced families. As Eran pointed out this would imply the hyperoptimistic conjecture. We can try to play with it.
So we have color classes and in each class the elements are ordered. We call a family of sets shifted if it is closed under replacing an element by a smaller element. One kind of shifting is to repeatedly choose to elements a and b in the same color class such that a<b and replace b by a for all sets that
(1) contain b and not b
(2) making the switch does not lead to a set already in the family.
Starting from a family F we get a new family Shift[a,b](F). We need to show that P(r,m) for F implies P(r,m) for Shift[a,b](F).
This seems too good to be true. But it can be useful to think about it for a while.
Since this is not the ordinary version of shifting it will also be useful to check if the balanced shifting of an intersecting balanced set is intersecting…
I thought that Shachar already gave a counterexample to this in https://gilkalai.wordpress.com/2015/11/03/polymath10-the-erdos-rado-delta-system-conjecture/#comment-22249
Oops, yes I missed Shachar’s comment. Right and its very simple. Actually the outcome of the shifting depends on the order you perform it in a very drastic way. Still we can ask if whenever we have a balanced family without a sunflower we can find some balanced shifting step keeping this property.
I think you can modify his example in the following way: k=2,r=3 and color sets {1,2,3} and {4,5,6}: {{1,4},{1,5},{2,6},{3,6}}. This does not contain a 3-sunflower but after any shift it does.
Right. I guess our most hyperoptimistic hopes regarding the hyperoptimistic conjecture cannot work. Actually we need some shifting procedure that will take somehow every collection of four edges into { 1 4} {1 5} {2 4} {2 5}.
After some discussion explaining the “total Betti number” to Gil, I think I should formulate some questions more clearly here. Let me first formulate two questions, and then give a more general argument for this approach in terms of higher laplacians, higher connectivity (as studied by Lubotzky and others) and an interesting duality that might be more attackable using homological or algebraic approaches.
First, via classical homology and cuts:
I consider any pure hypergraph of k-sets, and will think about it as a (k-1)-dimensional simplicial complex.
Question 1: What is the number of disjoint facets that can be found in a pure simplicial complex with total Betti vector b? What are the extremal examples?
Now, we can iterate this over the links, and if we find a large disjoint set in some link, we are done.
Question 2: If the Betti numbers are small in every link, what can the complex be?
Here I would imagine some approach via Hodge theory would help; if the complex has no reduced homology; then I would image we should be able to use higher laplacians to show that we can efficiently cut the complex into different components.
As mentioned, I think this is a symptom of a principle that can be formulated as follows: If the set family is highly connected, then every “cut” must be complicated and large, and in this cut we find a sunflower by induction.
If the complex is very sparsely connected, it is easy to cut the complex into parts, and be done with it.
Can you please share this explanation on the betti numbers here as well? I have to admit that I don’t really know what these are…
I think it will be useful to have a look at the 1972 paper by Abott, Hanson, and Sauer which improved both upper and lower bound of Erdos and Rado, At the 1977 paper by Spencer, and the 1996 paper by Kostochka both giving substantial improvement, for the upper bound. (Unfortunately I dont have a link for Spencer’s paper but I will try getting it.)
I have a more precise version of the “fanciful idea” from earlier. I think I can prove a lemma that says something along the lines of that there exists a reasonably large subsystem where most of the intersections are of the same size. I haven’t checked the argument carefully, so it may be wrong, but here is a sketch.
First, let us define the energy of a system of -sets to be the average size of the intersection of two sets selected independently at random (with replacement). I call this the energy because it is the (suitably normalized)
-sets to be the average size of the intersection of two sets selected independently at random (with replacement). I call this the energy because it is the (suitably normalized) 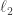 norm of the sum of the characteristic functions of the sets.
norm of the sum of the characteristic functions of the sets.
Suppose the energy is less than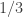 . (For simplicity I’m going to look just at the case where we are looking for sunflowers with three petals, but I’m not relying on that in a big way.) Then if I pick three sets
. (For simplicity I’m going to look just at the case where we are looking for sunflowers with three petals, but I’m not relying on that in a big way.) Then if I pick three sets  at random from the system I get that the expectation of
at random from the system I get that the expectation of 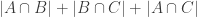 is less than 1, so there exist three disjoint sets.
is less than 1, so there exist three disjoint sets.
Therefore, the energy lies somewhere between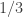 and
and  .
.
Now suppose that the energy lies between and
and 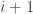 . (I’ll assume that
. (I’ll assume that  — the case of energy lower than 1 will need a similar but not identical argument.) I shall try to find a family that consists of at least 1% of the sets such that the energy increases by a factor of at least
— the case of energy lower than 1 will need a similar but not identical argument.) I shall try to find a family that consists of at least 1% of the sets such that the energy increases by a factor of at least  . (The numbers here are of course completely arbitrarily chosen.) If I can’t, then I have a seemingly quite strong property: that the average intersection size is around
. (The numbers here are of course completely arbitrarily chosen.) If I can’t, then I have a seemingly quite strong property: that the average intersection size is around  , but I can’t find a subsystem for which the average intersection size is even slightly bigger. That also feels like a kind of quasirandomness property that ought to be useful.
, but I can’t find a subsystem for which the average intersection size is even slightly bigger. That also feels like a kind of quasirandomness property that ought to be useful.
If I can find such a family, then I pass to it and iterate. There are at most iterations, so by the end I have dropped down to a family of at least
iterations, so by the end I have dropped down to a family of at least  times the original number of sets, and now I have a quasirandomness property.
times the original number of sets, and now I have a quasirandomness property.
I don’t have any feel for whether the quasirandomness property is actually helpful, but at this stage I’m just trying to justify my hunch that something vaguely along the lines of “we can get most intersections to be of roughly the same size” might be true.
Maybe I should spell out why the property I talked about in my previous comment is a quasirandomness property. Suppose you have a system A of k-sets. (NB, A is a collection of k-sets and not an individual k-set. I just don’t feel like typing the whole time.) Now partition A into B and C. If |B|=r and |C|=s, and if we write E for energy, then we get
the whole time.) Now partition A into B and C. If |B|=r and |C|=s, and if we write E for energy, then we get

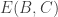 is the mutual energy, that is, the average size of the intersection of a random set in B with a random set in C.
is the mutual energy, that is, the average size of the intersection of a random set in B with a random set in C.
where
If B and C are reasonably large, and if it is impossible to increase the energy by much if we pass to a large subsystem, then and
and 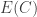 can’t be much bigger than
can’t be much bigger than 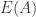 , from which it follows that all of
, from which it follows that all of  ,
, 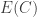 and
and 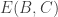 are approximately equal to
are approximately equal to 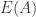 . But then, writing
. But then, writing 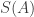 for the sum of the characteristic functions of the sets in
for the sum of the characteristic functions of the sets in  , and similarly for
, and similarly for  and
and  , we get that
, we get that  , from which it follows that
, from which it follows that  and
and 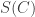 are approximately proportional to each other, and hence also approximately proportional to
are approximately proportional to each other, and hence also approximately proportional to 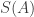 . So we have the following quasirandomness property: the sum of the characteristic functions of the sets belonging to any largish subcollection of
. So we have the following quasirandomness property: the sum of the characteristic functions of the sets belonging to any largish subcollection of  must be approximately proportional to the sum of the characteristic functions of all the sets in
must be approximately proportional to the sum of the characteristic functions of all the sets in  .
.
I will continue this discussion in a subcomment.
I claim that the behaviour I have just described is similar to the behaviour of a random system. To describe the random system it will be convenient to go for the multipartite model. Suppose, then, that we have sets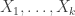 and a probability distribution on each one. To choose a random k-set, I choose a random element from each
and a probability distribution on each one. To choose a random k-set, I choose a random element from each 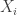 independently for each
independently for each  according to the given probability distributions. I then do that
according to the given probability distributions. I then do that  times, again independently, to create a system
times, again independently, to create a system  of
of  k-sets.
k-sets.
I don’t have a proof at the moment, but I think that for suitable ranges of various parameters, a system created this way will have the property that if you choose a large subcollection of sets from , the sums of its characteristic functions will be close (in a suitably normalized
, the sums of its characteristic functions will be close (in a suitably normalized 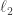 sense) to the appropriate multiple of the same thing for
sense) to the appropriate multiple of the same thing for  , which will just be
, which will just be  times the probability distribution on
times the probability distribution on 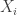 inside each
inside each 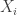 .
.
So what I hope is that we can pass to a system of sets that looks random in a useful sense.
If that is correct, then there are some obvious questions that I think should be easy to answer and fairly helpful. One is to see whether the following (informal) statement is true: given arbitrary sets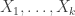 and arbitrary probability distributions
and arbitrary probability distributions  on them, if you choose your set system
on them, if you choose your set system  by picking
by picking  independent random sets from the product distribution, then you get a sunflower of size 3 when
independent random sets from the product distribution, then you get a sunflower of size 3 when 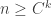 .
.
One could start with the simplifying assumption that the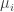 are uniform, so the only parameters to be chosen are the sizes of the
are uniform, so the only parameters to be chosen are the sizes of the 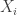 (which could be chosen to be equal if one wanted to simplify yet further).
(which could be chosen to be equal if one wanted to simplify yet further).
For this problem it is probably convenient to allow sets to occur in with multiplicity greater than 1 and to allow sunflowers with heads of size
with multiplicity greater than 1 and to allow sunflowers with heads of size  and petals of size 0.
and petals of size 0.
If random systems of this kind cannot give good examples, the hope would be to prove the (harder!) statement that neither can quasirandom systems that resemble the random systems.
The random case is indeed easy to analyze. For each distribution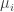 which has an element with probability
which has an element with probability  (say) lets condition on this element being chosen. This would only reduce probabilities by at most
(say) lets condition on this element being chosen. This would only reduce probabilities by at most  . So, lets assume from now on that the largest probability is
. So, lets assume from now on that the largest probability is  in each remaining
in each remaining 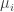 . Sample a set A; then, sample a second set B, conditioned on being disjoint from A; then, sample a set C, conditioned on being disjoint from A,B. The probability in each case of success is
. Sample a set A; then, sample a second set B, conditioned on being disjoint from A; then, sample a set C, conditioned on being disjoint from A,B. The probability in each case of success is  . So, with high probability after
. So, with high probability after  samples we will find the desired sets.
samples we will find the desired sets.
Thanks for that. Although it uses facts about random systems that are way stronger than one could extract from the quasirandomness notion above, it is still quite encouraging that that argument exists. Maybe to try to make it more in the spirit of a quasirandomness argument one should estimate the number of sunflowers there must be, given the distributions.
Pingback: Gil Kalai starts Polymath10 | Gowers's Weblog
Let me give a little explanation on looking at families of sets as geometric objects, homology groups and betti numbers. This is relevant to my approach that I will describe in detail next time, and also to Karim’s ideas. For my “plan” all we need is homology groups over a field which are vector spaces, and betti numbers are just the dimensions of homology groups.
Staring with a family F we will consider the collection of sets obtained by adding all subsets of sets in F. This is a simplicial complex, K, and we can regard it as a geometric object if we replace every set of size i by a simplex of dimension i-1. This is the motivation to call sets in K of cardinality (i+1) by the name i-faces. The definition of homology groups only depends on the combinatorial data. For simplicity we assume that all sets in F (and hence in the associated simplicial complex) are subsets of {1,2,…,n}. We choose a field A. Next we define for i>0 the vector space of i-dimensional chains as a vector space generated by i-faces of K. We also define a boundary map
as a vector space generated by i-faces of K. We also define a boundary map  for every i. The kernel of
for every i. The kernel of 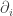 is the space of i-cycles denoted by
is the space of i-cycles denoted by  ; the image of
; the image of  is the space of i-boundaries, denoted by
is the space of i-boundaries, denoted by 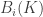 . The crucial property is that applying boundary twice gives you zero, and this allows to define homology groups
. The crucial property is that applying boundary twice gives you zero, and this allows to define homology groups  . The betti numbers are defined as
. The betti numbers are defined as  .
.
One can and should be skeptical that homology groups have anything to do with Erdos-Ko-Rado problems and the delta system conjecture. But I will try to give an appealing case that they might be relevant.
Indeed, Hao disproved the hyperoptimistic conjecture. This certainly support the view that some experimentation for small values of k and r can be instructive.
Here is a challenge for the readers: We made an analogy between “intersecting” and “acyclic”.
Building on this analogy
1) What could be the “homological” property analogous to “every two sets have at least m elements in common”?
2) What could be the “homological” property analogous to “not having r pairwise disjoints sets”?
Pingback: Polymath10 is now open | The polymath blog
I have a question that I think could well be answered with a simple counterexample.
Let be a system of
be a system of 
 -sets and suppose that the average intersection size of two sets in
-sets and suppose that the average intersection size of two sets in  is
is 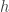 . Suppose also that at least
. Suppose also that at least 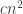 of the
of the 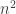 intersections are at least
intersections are at least  . Does it follow that there is a subsystem
. Does it follow that there is a subsystem  of
of  of size at least
of size at least 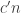 (with
(with 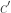 depending on
depending on  only) such that the average intersection size of two sets in
only) such that the average intersection size of two sets in  is at least
is at least  ?
?
If the answer is yes, then it enables us to pass to a system where almost all the intersections have the same size.
Here is an example that might be relevant. The sets correspond to lines in a projective space. But now, choose cn of the points at random and double them.
I don’t understand what you are saying here but would definitely like to. Would it be possible to define the example more formally?
(Maybe its nonsense). We start with the ordinary example when we have n points and n sets and the sets correspond to lines in a projective space so every set has $q+1$ elements and every two sets intersect in one element. Now we take
every set has $q+1$ elements and every two sets intersect in one element. Now we take 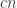 of the points and double them, namely add a clown to the point belonging to the same sets. Now some of the intersections are of size 2 rather than 1. In fact a fraction c of the intersections are now doubled. So this is the example. So now,
of the points and double them, namely add a clown to the point belonging to the same sets. Now some of the intersections are of size 2 rather than 1. In fact a fraction c of the intersections are now doubled. So this is the example. So now,  or so and for a fraction
or so and for a fraction  of pairs the intersection is 2. (It is not quite
of pairs the intersection is 2. (It is not quite  we can make it
we can make it  on the nose by tripling some points.) You want to find a subcollection of sets so the average intersection size is
on the nose by tripling some points.) You want to find a subcollection of sets so the average intersection size is  . It looks to me that this will not be possible but maybe I miss something.
. It looks to me that this will not be possible but maybe I miss something.
Just to check, when a set A contains a point x that has a double x’ added, what happens? We can’t just add x’ to the set A, since then A would have the wrong size. But we could create a set A’ = A – x + x’. But if we do that, then the intersections are still all of size at most 1.
Alternatively, maybe we do add the extra points to the sets (perhaps deleting sets that have more than one extra point added) and then add further extra points to all the other sets — a different point for each one.
That’s right. The expected size of a set will change from to
to  so I think we need to do something to make sure that all sets are of the same size. Maybe this does happen with small but positive probability and all other random behavior of the examples hold. (Actually it is sort of interesting if we can delete cn points leaving all sets of equal size.) And maybe we need to add some dummy all different points to all sets whose sizes are less than the maximum. Somehow it looks to me that this is dealable.
so I think we need to do something to make sure that all sets are of the same size. Maybe this does happen with small but positive probability and all other random behavior of the examples hold. (Actually it is sort of interesting if we can delete cn points leaving all sets of equal size.) And maybe we need to add some dummy all different points to all sets whose sizes are less than the maximum. Somehow it looks to me that this is dealable.
I agree that something like this seems to work. I’ll have a think about it and try to decide what morals can be drawn from it (assuming it really does work).
Another question that we can play with is the following. We saw that we can reduce the conjecture to the case of balanced families because the gap is only exponential. Are there others, perhaps more drastic, reductions of this kind?
This might be an obvious question, but to have a sunflower with three petals, is to find three sets $A,B,C$, so that $A \cap B \subseteq C$, and $C \cap (A \triangle B)=\emptyset$.
What happens if instead of both properties, just one of them is forbidden? For example, if we forbid three sets $A,B,C$ in our family, so that $C \cap (A \triangle B)=\emptyset$?
This time with latex code written properly:
This might be an obvious question, but to have a sunflower with three petals, is to find three sets , so that
, so that  , and
, and  .
.
What happens if instead of both properties, just one of them is forbidden? For example, if we forbid three sets in our family, so that
in our family, so that  ?
?
That’s a nice question! One could also ask to forbid something even weaker, namely three sets such that
such that 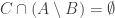 . To put it the other way, can we obtain an exponential upper bound for the number of
. To put it the other way, can we obtain an exponential upper bound for the number of  -sets you need in order to guarantee that there exist
-sets you need in order to guarantee that there exist  with
with 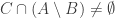 ?
?
Sorry, that last should be
should be  .
.
If we take sets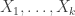 of size 2 and take the complete
of size 2 and take the complete  -partite
-partite  -uniform hypergraph with the
-uniform hypergraph with the 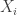 as the vertex sets (i.e., the standard lower bound for 3-sunflowers), it seems to be a lower bound for your question as well. That’s because if
as the vertex sets (i.e., the standard lower bound for 3-sunflowers), it seems to be a lower bound for your question as well. That’s because if  belongs to
belongs to 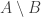 , then the other element of
, then the other element of 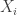 must belong to
must belong to  , so
, so  , which implies that every set intersects
, which implies that every set intersects  .
.
Actually, I think that bound is more or less tight. Let be a set in the system. If
be a set in the system. If 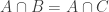 , then
, then  is disjoint from
is disjoint from  . So there can be at most
. So there can be at most 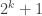 sets in the system.
sets in the system.
I think it’s exactly tight, since if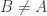 , then
, then  , getting rid of the
, getting rid of the 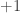 . Nice.
. Nice.
I’m thinking about what we forbid in terms of Venn diagrams. Here are the problems we discussed:
– In the sunflower question we forbid three regions in the Venn diagram to be empty, namely, those that are contained in exactly two out of the three sets.
-In the question you just solved, we forbid that at least two out of these three regions are empty.
-In the other variant you mentioned, we forbid that at least one of these three regions is empty. This last question is equivalent, by moving to the complement family, to the question studied here, where one forbids the union of two sets in the family to contain a third set in the family.
http://www.sciencedirect.com/science/article/pii/0097316582900048
Studying which Venn diagram configurations give an upper bound that depends only on the set size, k, and not on the size of the base set, seems interesting to me too. I’m not sure that I could follow which problem (“other variant you mentioned”) is equivalent to the problem you link to, but there the bound already depends on the size of the base set.
I’m trying to think (as I have already mentioned in comments above) what might possibly be achieved by regularization of the set system. Roughly speaking, by this I mean that a first step in a proof could be to pass to a subsystem that contains at least a proportion of the sets, such that we can understand the subsystem well because in some sense it “looks random”.
of the sets, such that we can understand the subsystem well because in some sense it “looks random”.
Experience with hypergraph regularity suggests that there should be some subtlety about this, however, and Gil’s example above reinforces that suggestion. I had wondered (expecting the answer no) whether one could pass to a subsystem where almost all intersections have roughly the same size. But for this I needed a lemma that said that if the intersections are not almost all roughly the same size, then one can pass to a subsystem containing a constant fraction of the sets such that the average intersection size goes up by at least some constant. Gil confirmed that this was indeed false. (We have not checked the example, but it certainly looks correct.)
I now want to try to understand more generally what counterexamples can look like, in the hope of formulating a more sophisticated conjecture — that is, a more sophisticated description of what a system must look like if you can’t pass to a constant fraction of the sets and increase the average intersection size by a positive constant. I’ll continue this discussion in some subsidiary comments.
This is a very interesting direction and in some sense the trick of moving to balanced families has some flavour of regularization. We can make a more drastic such move: we can color the original vertices by 100k colors and choose only randomly chosen set of k colors. This may have some regularization property but perhaps its too easy to be useful.
Here is a question I dont know the answer to.
Question: can color the ground set with 100k colors and by taking an exponentially small fraction of the sets make sure that every pair of vertices of the same color are far-apart?
What does “far apart” mean here?
This is negotiable. you can ask in terms of the dual distance between two vertices of the same color. (The dual graph is the graph whose vertices are sets and two vertices are adjacent if the two sets share k-1 elements). You can also ask in terms of the largest set A that have two vertices of the same color in its link.
So perhaps the simplest version is that two vertices of the same color are in dual distance at least c.
In these subsidiary comments, I want to try to define some nice counterexamples to go with Gil’s. The ultimate aim is to find some good property they have in common and find a plausible conjecture about what all counterexamples must look like (after one has passed to an appropriate subset to regularize).
The first possible counterexample is very simple, and close in spirit to Gil’s: pick random -subsets of a set of size
-subsets of a set of size 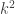 . The probability that two such subsets intersect is around
. The probability that two such subsets intersect is around  , and I think the intersection size will be roughly Poisson with mean 1. It doesn’t look to me as though one can do much to change this distribution by passing to 1% of these sets. (For example, we can’t do something simple like choosing all the sets that contain some particular element.)
, and I think the intersection size will be roughly Poisson with mean 1. It doesn’t look to me as though one can do much to change this distribution by passing to 1% of these sets. (For example, we can’t do something simple like choosing all the sets that contain some particular element.)
The second example I wanted to give is slightly more interesting. Let us choose a random graph with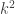 vertices and bounded average degree
vertices and bounded average degree 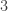 . Now choose random
. Now choose random  -sets by picking a vertex and taking a random walk from that vertex and letting the set be the first
-sets by picking a vertex and taking a random walk from that vertex and letting the set be the first  steps of the walk. (Discard any walks that visit the same point more than once.)
steps of the walk. (Discard any walks that visit the same point more than once.)
The resulting -sets should be very spread around, but also have the property that if two of them intersect at an interior point of both walks, which is what usually happens, then the intersection will usually be of size at least 2 (because the vertex typically has degree at most 3), and quite likely even greater than 2. But the average intersection will again be 1 I think.
-sets should be very spread around, but also have the property that if two of them intersect at an interior point of both walks, which is what usually happens, then the intersection will usually be of size at least 2 (because the vertex typically has degree at most 3), and quite likely even greater than 2. But the average intersection will again be 1 I think.
So in this case, it looks as though we have a substantial number of intersections of size 2 and a substantial number of size 0, and it doesn’t seem easy (unless I’m missing something) to change this by passing to a subsystem consisting of 1% of the sets.
Here’s one reason I want to try to understand this kind of example. It stems from a proof attempt that doesn’t seem to work. I’ll give the proof attempt in some detail, to try to make it seem vaguely plausible.
For each let
let 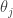 be the probability that the intersection of two random sets from the system is of size at least
be the probability that the intersection of two random sets from the system is of size at least  . If
. If  then we get a sunflower of size 3, so we may assume that
then we get a sunflower of size 3, so we may assume that 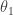 isn't tiny.
isn't tiny.
Now let us try to find such that
such that  . If we can't, then
. If we can't, then  . So if the number of sets is
. So if the number of sets is 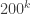 then we get lots of identical sets, which gives us lots of (somewhat degenerate) sunflowers. Alternatively, if we insist that all sets are distinct, we just get a contradiction.
then we get lots of identical sets, which gives us lots of (somewhat degenerate) sunflowers. Alternatively, if we insist that all sets are distinct, we just get a contradiction.
So we may assume that we have such a . Now choose a random
. Now choose a random  from the system. Then on average there will be at least a proportion
from the system. Then on average there will be at least a proportion  (or something like that) of the sets that intersect
(or something like that) of the sets that intersect  in at least
in at least  , and a fraction at least
, and a fraction at least 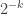 of these will have the same intersection with
of these will have the same intersection with  .
.
What I would like to be able to say at this point is that because not very many intersections have size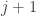 , within this collection of sets most of the parts outside
, within this collection of sets most of the parts outside  must be disjoint. But that fails because we've passed to a small set.
must be disjoint. But that fails because we've passed to a small set.
That still leaves the possibility that it could be true on average, but this still fails because it could be that once we know that a whole collection of sets all contain some set of size , the correlations in the system make it much more likely that they will have larger intersections.
, the correlations in the system make it much more likely that they will have larger intersections.
It might be worth trying to disprove the sunflower conjecture by creating a set system of this kind, where once sets start to intersect they are more likely to continue to do so. That is what makes me interested in the strange example with the paths in a random graph, which has that quality in a weak way.
A couple of observations:
1. suppose we can find a subfamily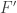 , so that the intersection of any two sets in
, so that the intersection of any two sets in 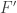 is exactly
is exactly  . Then the size of
. Then the size of 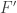 is at most
is at most  . Indeed, assume otherwise. Take any set
. Indeed, assume otherwise. Take any set 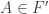 , and look at all the intersections
, and look at all the intersections 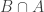 for all $\latex B \in F’$. Then by the pigeon hole principle, we can find
for all $\latex B \in F’$. Then by the pigeon hole principle, we can find 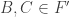 , so that
, so that  . But then we have also that
. But then we have also that  , since we know that the intersection sizes are all the same for pairs of sets in
, since we know that the intersection sizes are all the same for pairs of sets in  , and we get a sunflower.
, and we get a sunflower.
2. Suppose the average intersection size in our family is linear in
is linear in  . Then we can find a subfamily which is a star $\latex F’ \in F$ with head size linear in
. Then we can find a subfamily which is a star $\latex F’ \in F$ with head size linear in  , say
, say  latex |F’|>2^{-k}|F|$. Now the link of $\cap F’$ is a sunflower-free family for
latex |F’|>2^{-k}|F|$. Now the link of $\cap F’$ is a sunflower-free family for  latex 2^k$, so we could use induction. That is, we got
latex 2^k$, so we could use induction. That is, we got 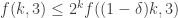 .
.
typo corrections (I’ll get used to this wordpress latex eventually).
A couple of observations:
1. suppose we can find a subfamily , so that the intersection of any two sets in
, so that the intersection of any two sets in 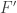 is exactly
is exactly  . Then the size of
. Then the size of 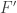 is at most
is at most 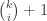 . Indeed, assume otherwise. Take any set
. Indeed, assume otherwise. Take any set 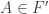 , and look at all the intersections
, and look at all the intersections 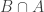 for all
for all 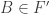 . Then by the pigeon hole principle, we can find
. Then by the pigeon hole principle, we can find 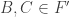 , so that
, so that  . But then we have also that
. But then we have also that  , since we know that the intersection sizes are all the same for pairs of sets in
, since we know that the intersection sizes are all the same for pairs of sets in 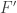 , and we get a sunflower.
, and we get a sunflower.
2. Suppose the average intersection size in our family is linear in
is linear in  . Then we can find a subfamily which is a star
. Then we can find a subfamily which is a star  with head size linear in
with head size linear in  , say
, say  and
and 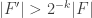 . Now the link of $\cap F’$ is a sunflower-free family for
. Now the link of $\cap F’$ is a sunflower-free family for 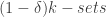 , and the size decreased only by a factor of
, and the size decreased only by a factor of 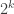 , so we could use induction. That is, we got
, so we could use induction. That is, we got 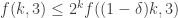 .
.
I’ve been thinking along somewhat similar lines, which is why I was interested in families for which almost all the intersections are the same size — or even roughly the same size.
I think that with remarks 1 and 2 one can begin to build up a picture of what a counterexample would have to look like. It would need the following properties.
(i) The average intersection size is very small (but not so small that you can easily find a sunflower consisting of disjoint sets).
(ii) Once you know that a collection of sets all have a common point, then the average intersection size goes up significantly.
The idea here is that the simple pigeonhole argument should in some sense be “sharp”. (I put the inverted commas because it is known not to be exactly sharp, but I mean it in a much vaguer way.) So the set system then “thwarts” us as we try to pass to better families. Initially, say, the expected intersection size is around 1. So we then pick a whole lot of sets all containing some element x, in the hope that because average intersections are 1, the sets we now have should have a strong tendency to be disjoint. But in fact they don’t, because in this subcollection the average intersection size has gone up to 2 (including x).
The strange thing is that up to a point this is what we would expect for a purely random system of sets. If we choose random -sets from
-sets from  , then a typical intersection will have size 1, but if you pick a typical pair of sets that contain
, then a typical intersection will have size 1, but if you pick a typical pair of sets that contain  , then the remaining
, then the remaining 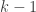 points in each set will also tend to intersect in about 1, and so on, at least for a little while.
points in each set will also tend to intersect in about 1, and so on, at least for a little while.
This doesn’t lead to a counterexample in an obvious way because it is too easy to find disjoint sets. But it does make me wonder whether we should try to find a set system that gives a very slightly greater than exponential bound.
Another plausible approach to find such families is to run a “Sunflower-free process” analogous to the triangle-free process or more generally the $H$-free process. We start by choosing any k-set and keep adding k-sets, one by one, uniformly at random out of those that do not form a sunflower with the sets already in our family and stop when we have reached a maximal sunflower free family. One would expect that, with high probability, the family you obtain this way has the property that passing to a large subfamily will not be useful in the sense that the sets will be anymore this disjoint. Understanding the process seems quite an interesting question of its own right, in particular if one can show that it is possible to get exponentially many sets in this way!
I very much agree with this — including about the question being interesting in its own right — and had had a similar thought myself.
I think it would even be interesting to try to make heuristic guesses about what should happen. There is of course an initial choice one needs to make about the size of the ground set. I think there are two natural candidates. One, if one is going for gold, so to speak, is to take a ground set of size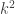 . But if one just wants a very slightly superexponential family, then it could make sense to go for a set of size
. But if one just wants a very slightly superexponential family, then it could make sense to go for a set of size  for some
for some  such that
such that  quite slowly. (One could e.g. take
quite slowly. (One could e.g. take  .)
.)
What is likely to happen when we do this? I’ll consider each option in turn and stop when I get stuck.
With the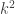 option, we’ll find that for any two random sets there’s a good chance that they are disjoint, so right from the start the sunflower-free process is very different from a purely random process. For instance, in a constant number of steps we will have two disjoint sets, and every further set we add will be constrained to intersect one of them. But that won’t be all. Let’s suppose, for example, that the first two sets
option, we’ll find that for any two random sets there’s a good chance that they are disjoint, so right from the start the sunflower-free process is very different from a purely random process. For instance, in a constant number of steps we will have two disjoint sets, and every further set we add will be constrained to intersect one of them. But that won’t be all. Let’s suppose, for example, that the first two sets  and
and  are disjoint (as they easily could be). Then it is still the case that two further sets have a good chance of being disjoint, since the fact that they both intersect
are disjoint (as they easily could be). Then it is still the case that two further sets have a good chance of being disjoint, since the fact that they both intersect 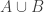 makes a rather small contribution to the probability that they intersect each other. Also, if a new set
makes a rather small contribution to the probability that they intersect each other. Also, if a new set  intersects
intersects  but not
but not  , then all further sets are constrained to intersect
, then all further sets are constrained to intersect  as well as
as well as 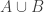 .
.
I’m already feeling a bit stuck, but in general when we’ve chosen a number of sets we’ll find that there are a whole lot of disjoint pairs. These will form a system of -sets, and all further sets will have to be transversals for this system. We also know that this system forms an intersecting family. In fact, it forms a 2-intersecting family. At this point things start to get a bit hazy for me: if we have a fairly random 2-intersecting family, how easy or hard is it for a new
-sets, and all further sets will have to be transversals for this system. We also know that this system forms an intersecting family. In fact, it forms a 2-intersecting family. At this point things start to get a bit hazy for me: if we have a fairly random 2-intersecting family, how easy or hard is it for a new  -set to be a transversal for the family? Given that the family is fairly random, one might expect it to be quite spread out, so that no point is contained in too many of the sets, in which case it would be quite hard. But if it is too hard, then how would the sets be a 2-intersecting family?
-set to be a transversal for the family? Given that the family is fairly random, one might expect it to be quite spread out, so that no point is contained in too many of the sets, in which case it would be quite hard. But if it is too hard, then how would the sets be a 2-intersecting family?
I don’t really know what to say here. In the other case, the probability of two sets intersecting is very high, so the sunflowers that are likely to cause trouble will probably have quite big heads. Indeed, if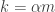 , then I would guess that the normal size of a head of the first sunflower that causes a set to be rejected would be of roughly size
, then I would guess that the normal size of a head of the first sunflower that causes a set to be rejected would be of roughly size  .
.
One other remark before I finish this comment is that if I get time, I am very tempted to write a quick program to implement this process for various values of and
and  to get a feel for how many sets it ends up producing, though if it does what we want and gives us exponentially many or maybe even more, then it won’t be possible to make
to get a feel for how many sets it ends up producing, though if it does what we want and gives us exponentially many or maybe even more, then it won’t be possible to make  very big.
very big.
Pingback: Polymath10, Post 2: Homological Approach | Combinatorics and more
First: thank you for writing all this!
Second: perhaps I’m missing something but it seems that the notion of an ‘intersecting’ family is never defined, in spite of the large role it plays in the text. Can I safely assume that it means that the family does not contain a pair of disjoint members, or is something more fancy going on?
(The first appearance of an intersecting family is in the Erdös-Ko-Rado Theorem (assuming that the word ‘family’ accidentally disappeared from that theorem but should be there) and the context surrounding it leaves the impression that you might be interested in a weaker condition where the family is already intersecting when for some number $r$ there are no r-member subfamilies all whose members are disjoint. On the other hand there is the ‘r = 2’ in the Erdös-Ko-Rado theorem that suggests perhaps just the naive definition of intersecting is intended.)
Dear Vincent, A family of sets is “intersecting” if every two sets in the family has non empty intersection. (I will add this explanation to the text.)
I am wondering what are the best bounds known / that we can get on the following special case. Consider a balanced family (e.g. there are k color sets, and each set contains exactly one element from each color set). Assume furthermore that each color set has size m. What is the maximal size of a 3-sunflower-free family? how does it scale with m? two interesting special cases to consider: m=O(1) and m=poly(k).
These are good questions. In the non balanced case there was a lot of study on the case that we are talking about subsets oh {1,2,…,n} (allowing sets of different sizes or considering sets of size n/2). The is referred to as the weak delta system question. See Kostochka’s surveys. For the balanced case I don’t know if it was studied.
Hi, I am not a professional mathematician and I do not know LaTex, and I’m a little nervous about asking. But I am trying to get a feel for the problem statement.
Is there perhaps a relation between the PolyMath 10 problem and the card-game Spot-it? Spot-it is a card-game wherein there are 55 cards, each card has about 8 different symbols (bulls-eye’s, ghosts, anchors, clocks, etc.) Under a simple construction I believe related to the Ray-Chaudhuri–Wilson theorem, any two cards have exactly one common symbol. The game, as it were, is to identify as quickly as possible the common element. My 7 year old can often catch it before me.
There are plenty of collections of 3 cards that have one (and only one) common symbol.
Is constructing a small Spot-it deck in a sense a dual of the Erdos-Ko-Rado theorem?
Thank you very much, and looks like a nice project.
Dear Mark, The mathematical construction behind the game you described seem closer to combinatorial designs than to Erdos-Ko-Rado theory but it is still related topics. Here is a related link http://math.stackexchange.com/questions/36798/what-is-the-math-behind-the-game-spot-it
Dear Gil, thank you very much for the nice link! I understand a lot better now.
Thanks Gil for organising this interesting blog. Thinking about what might be learnt from small cases:-
If k=2, then the key configuration for maximising the number of sets is effectively just two ‘complete’ families of 2-sets each on its own r letters. Is it known what the key configurations are for k=3, …?
It is not correct that the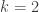 case can be solved in that way. For example if you take all 2-sets on four numbers/letters then two disjoint subsets can already be found, so two the complete families have flowers with an empty head and four petals.
case can be solved in that way. For example if you take all 2-sets on four numbers/letters then two disjoint subsets can already be found, so two the complete families have flowers with an empty head and four petals.
This is what I know about the small cases.
 is one set of k elemeents
is one set of k elemeents
 Take two sets of size three with empty intersection and take all the subsets of size two from both. This gives the 6 sets required.
Take two sets of size three with empty intersection and take all the subsets of size two from both. This gives the 6 sets required.
 There are several distinct solutions involving 6, 7 or 8 elements
There are several distinct solutions involving 6, 7 or 8 elements
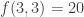 Take a dodecahedron and label the 12 faces with numbers from 1 to 6 such that opposite faces have the same number. Form a set for each vertex of the dodecahedron consisting of the three numbers on the faces meeting at the vertex. This gives ten distinct sets. The other ten sets repeat the same pattern but with 6 different numbers.
Take a dodecahedron and label the 12 faces with numbers from 1 to 6 such that opposite faces have the same number. Form a set for each vertex of the dodecahedron consisting of the three numbers on the faces meeting at the vertex. This gives ten distinct sets. The other ten sets repeat the same pattern but with 6 different numbers.
I don’t know any other exact results
For small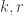 the problem gets too hard too quickly to shed much light. I suggest that it might be useful to consider a generalisation in which the maximum number of petals is a given function of the size of the head. This means that instead of one number
the problem gets too hard too quickly to shed much light. I suggest that it might be useful to consider a generalisation in which the maximum number of petals is a given function of the size of the head. This means that instead of one number  there are now
there are now 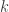 numbers
numbers  . The problem then is to find the maximum number of k-sets such that there is no sunflower with a head of size
. The problem then is to find the maximum number of k-sets such that there is no sunflower with a head of size  and
and  petals for any
petals for any 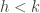 . There are cases that may be tractable and still helpful with understanding the problems when most of the
. There are cases that may be tractable and still helpful with understanding the problems when most of the  are equal to 2, while a few are equal to 3.
are equal to 2, while a few are equal to 3.
This can be investigated for small numbers either by hand or by computer. When searching for maximal collections of k-sets, you can use the fact that any possible set you would add to a maximal collection would have to form a disallowed sunflower. This allows you to search for maximal sets using sudoku-like rules to build up possible collections.
Pingback: Polymath 10 Post 3: How are we doing? | Combinatorics and more
Pingback: attack on/ of the sunflowers! | Turing Machine
I have stupid questions on the function , which are mostly caused by not having an overview over all the comments.
, which are mostly caused by not having an overview over all the comments.
Question 1: There are some simple inequalities such as ,
, 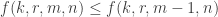 ,
,  and
and  . Of course one can improve these inequalities without much effort. Did, by any chance, someone already do this and wrote it down in one of the comments/somewhere else?
. Of course one can improve these inequalities without much effort. Did, by any chance, someone already do this and wrote it down in one of the comments/somewhere else?
Question 2: If we have a largest example for , for which
, for which 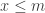 can we then guarantee the existence of a sunflower
can we then guarantee the existence of a sunflower  with
with  ? I am sure that
? I am sure that 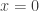 , because otherwise the problem is much easier.
, because otherwise the problem is much easier.
I did not think too much about this. I just think that they are already answered somewhere.
The one simple formula should be of course something like , not
, not  .
.
Q1: I don’t think anyone made such a collection yet, I wonder if there are interesting inequalities where on both sides you have only “one f”.
Q2: This (also) seems to have some typo.
Q1: thanks.
Q2: It should always be . I just want to know if we can guarantee the existence of specific link-sizes. Makes computer searchers a bit faster.
. I just want to know if we can guarantee the existence of specific link-sizes. Makes computer searchers a bit faster.
So is Q2 whether there are r-1 disjoint sets in a maximal family? If so, then yes, otherwise you could add a new set that’s disjoint from the whole family.
It sounds like a good idea to collect things that make computer searches faster.
I meant all sunflowers with kernel/head/link size 1, 2, ,3, …, k-1? I suppose that there all must exist in the largest examples, but besides link size 0 it is not obvious to me. For EKR sets for different structures you can sometimes make nice arguments that all/many relations occur in the largest example.
Pingback: Polymath10-post 4: Back to the drawing board? | Combinatorics and more
Pingback: A title – to be defined
I want to create a site where it’s a one stop shop for stories and articles on a particular subject….as long as I give credit to the author or source will I be ok, I will not steal original content, but rather gather it…is this legal?.
Pingback: Polymath10 conclusion | Combinatorics and more
Pingback: Hardness of Approximating Vertex Cover, Polytope-Integrality-Gap, the Alswede-Kachaterian theorem, and More. | Combinatorics and more
Pingback: Amazing: Ryan Alweiss, Shachar Lovett, Kewen Wu, Jiapeng Zhang made dramatic progress on the Sunflower Conjecture | Combinatorics and more
Pingback: Proposals for polymath projects – Math Solution
Pingback: Greatest Hits 2015-2022, Part I | Combinatorics and more