Update (April 2016) : Here is a link to a new post on my May 2016 Notices AMS paper.
Here are links to a videotaped lecture in two parts entitled “why quantum computers cannot work” recorded at the Simons Institute for the Theory of Computing on December 2013 and two additional videos: a short talk on topological quantum computers and a twelve minute overview. Here are the links: Overview, Part I, Part II, Topological QC. (Update, Nov 14: BosonSampling.)
Why Quantum Computers Cannot Work:
Overview and Vision.
Why Quantum Computers Cannot Work I:
From the “Trivial Flow” to Smoothed Lindblad Evolutions
Why Quantum Computers Cannot Work II:
Debate, Reasons to Disbelieve, and Experimentation
Why Topological Quantum Computers Cannot Work
The Geometry of Spacetime is Enabled by the Failure of Quantum Fault-Tolerance
Left: Nick Read; Right The front page of Nick’s 1990 famous paper with Greg Moore on nonabelions, and below his email to me from March 2005 on topological quantum computation. (click for full view.)
Left: the argument regarding topological QC demonstrated via Harris’ famous cartoon. While not strictly needed I expect the argument to extend from qubits to gates as well. Right: a recent discussion with Nick over Shtetl Optimized (click for full view). Update: We are actually not in an agreement as it seems from the above discussion (see the discussion below).
Update (Nov’ 2014): A fifth video, this time in front of a live audience
Complexity and Sensitivity of Noisy BosonSampling
Update: A subsequent post by Steve Flammia, Quantum computers can work in principle over The Quantum Pontiff. (July:) See also this post: Quantum future” just beyond our grasp.
And a lecture at the Technion from 2015 in Hebrew!
Added later (April 18): Let me quote from what Steve wrote about the videos: The surprising part is the superior production value relative to your typical videotaped lecture (at least for the first overview video). Producing the videos was an interesting and demanding experience and I was certainly happy to read Steve’s description of the production value. (Of course, the main purpose of Steve’s post was to express his disagreement with the content of the videos. See either the post or Co-‘s comment below.)
Also there are two earlier versions of my lecture (in 1-hour format) that were videotaped. The first was taken by Jesus De Loera in Davis. Very interesting shooting-angle and interesting comments by Greg Kuperberg, Bruno Nachtergaele and other participants. The second was taken in Seattle in a UW-PIMS colloquium lecture. Again interesting questions by several participants including James Lee and John Sidles.
(July:) The Simons Institite (almost identical) versions of the movies are now linked from the web-page of my November 15 lecture at SI.
(Added nov 2014): The only difference from the HUJI version is that there are no opening slides and that for the closing slides I used two pictures of my department’s administrative staff.
The administrative crew of the Einstein Institite of Mathematics (click to enlarge)
I thought of it as a nice opportunity to thank our great administrative staff whose part is crucial in the academic endeavor, and this is a good opportunity to thank the staff in my second academic home – Yale University, in the Simons Institute, in many other places.
Alistair Sinclair and the Simons Institure friendly and helpful staff (click for full size)
Following Saharon Shelah: How to watch these videos
(Added Nov 2014)
Saharon Shelah explained in an introduction to one of his books, that instructions on “how to read this book” are actually instruction on “how to not read this book”. If you want to read the book you start on page 1 and read through to the last page. Instructions for “how to read this book” rather tell you how to jump to a place that interests you.
So, in a similar spirit, here are direct links to the different parts of the videos.
Why quantum computers cannot work: Video I:
A brief description of the lecture 0:00-7:50 (Click here to the start)
Part I: Quantum computers 7:50 -12:48 (Click here to start)
Part II Noise, quantum fault tolerance, the quantum fault tolerance barrier, and the “trivial flaw.” Noise, quantum fault tolerance 12:48-16:40; The quantum fault tolerance barrier 16:40; The “trivial flaw” 19:11-27:40.
Part III My conjectures 27:10
(Two qubits behavior; error synchronization; encoded single qubits; Shor/Sure separators and rate.)
Part IV: Smoothed Lindblad evolutions 40:31
(The definition of smoothed Lindblad evolutions, The work with Kuperberg, Response to some concerns, The internal clock of the evolution; physical mechanism)
Ending – Dorit Aharonov’s comment and my response 57:50 .
Why quantum computers cannot work – Video II:
Part V: Conceptual points from the debate 0:00 ;why are classical computers possible? 4:23, locality 7:49, classical simulation of quantum physics 9:19, (typo: “you see it in complexity” should be “you see it in cryptography”) Does no QC means breakdown of QM? 11:41 The story about Kelvin dating the earth 11:53; to which ares of physics impossibility of quantum fault tolerance are relevant 16:38 .
Short Part VI: Quantum computation without quantum fault-tolerance 18:22
Part VII: Reasons to disbelieve, experiments and summary 27:53
Seven reasons for disbelief; Can you hear the shape of a quantum computer?; Can you reverse or permute the arrow of time? noise and symmetry.
Experimentation 34:40: Martinis and other’s attempts at stable qubits based on surface codes, sub-gaussian fluctuations for error-rates in interacting systems.
Summary 39:46
Pictures from the debate 40:21 (including a few unrelated pictures like a forgotten picture of Avi Wigderson and Oded Goldreich).
Entertaining/educating parts of the debate 49:33 (Including Scott’s famous $100,000 challenge; Aram’s 3-SAT and 2-SAT analogy, a heart breaking eulogy for Conjecture C ; Jesus and the camel, Making formal distinctions, Aram 3-SAT/2-SAT analogy revisited)
Answers to questions 59:51
If it is up to me will I choose QC to exist? Do I build my work on the assumption that QC are impossible? Is the title of the lecture too strong? If there is a physical principle of “no quantum fault tolerance” how come it was not observed before?
Thanks; Ending presentation.
Why quantum computers cannot work – Overview Video:
Introduction (0:00); From the debate (2:41); The trivial flaw; Gil’s alternative; Reasons to disbelieve (4:03) ; Experimentation (6:41); Insights to physics and conclusion(8:37)
Why topological quantum computers cannot work
Introduction (0:00) ; The simulation argument (1:34); Other case for which the simulatuin argument applies (4:37); Quantum fault tolerance and geometry (5:52); The vicious circle for quantum computations and new phases of matters (7:20); Directions for further research (11:32) ; philosophical ending (13:17)
Combinatorics and more 
For beginners like me who need help with some of the vocabulary used here, such as “anyon,” you can look at:
http://www.quantiki.org/wiki/Anyons
or
http://en.wikipedia.org/wiki/Anyon
Thanks, Joe! Anyons are indeed fascinating objects related to deep mathematics. For the connection to quantum computing see, for example, this review paper by Chetan Nayak, Steven H. Simon, Ady Stern, Michael Freedman, and Sankar Das Sarma.
My fourth video describes an argument for why we cannot expect that anyonic qubits will be more stable then ordinary qubits. I think that this argument extends to anyonic gates as well. It would be interesting to consider in detail proposed implementations like those in the review paper above.
This argument does not say anything about the fascinating question whether nonabelions are realistic. But the second part of the fourth video may be related to this question. There is some hope that we one can show that nonabelions (of low entropy) requires for their creation quantum fault-tolerance. Another thing that I am interested to know is to what extent the noise-sensitivity argument for Bosonic (and fermionic) states from the second long video (part VI) can be extended to anyons. The difficulty is that we do not have analogs of “decomposible” states like in the case of exterior and symmetric algebras.
Gil, I have posted the following appreciation of your (wonderful) lectures to the Quantum Pontiff weblog of Dave Bacon, Charlie Bennett, Steve Flammia, and Aram Harrow. There is plenty of room for *ALL* of you to be right (as it sems to me). Good!
————–
It All Turns on Naturality (Part I of II)
Steve, please let me make the case (to students especially) that rational grounds exist to to disagree utterly with all six of the above statements.
Moreover, please let me assert (more broadly) that it is neither necessary, nor feasible, nor even desirable, that everyone think alike in regard to any of these six statements.
And finally — and most difficult of all — please let me make this case without personalization, sardonicism, rancor, or cherry-picking.
Because we’re talking about ideas, not individuals, right?
Warmup A recommended four-part counter-sardonic warmup is, first, to listen to the Van Cliburn Foundation’s playlist “2013 Cliburn Competition Competitors” (queue up all 30 videos, and reflect upon the sobering statistical realities of excelling as an artist/mathematician/scientist/engineer on a planet of 10^10 people). Second, listen to Wendell Berry’s 2012 Jefferson Lecture “It All Turns on Affection” (reflecting soberly upon the “marketplace of ideas”). Third, (re)read Clay Shirky’s much-discussed “The End of Higher Education’s Golden Age” (reflecting soberly upon how “Golden Ages” are created).
Fourth, and most important, (re)read Arthur Jaffe and Frank Quinn’s sardonic and sometimes-personal “‘Theoretical Mathematics’: Toward a Cultural Synthesis of Mathematics and Theoretical Physics” (arXiv:math/9307227), and Bill Thurston’s straightforwardly impersonal response “On Proof and Progress in Mathematics” (arXiv:math/9404236) (reflecting soberly that all of the Jaffe/Quinn/Thurston issues are in-play in the context of modern complexity theory and/or quantum computing).
These great works (Bill Thurston’s especially) set the stage for us to appreciate the concluding remarks of Gil’s video lecture (minute 13:16 of “Why Topological Quantum Computers Cannot Work”)
In a Nutshell Gil Kalai brings the generous & vital spirit of Bill Thurston to discourse regarding quantum computing and complexity theory … and for this service we can all be grateful to Gil!
—–
Part II (to follow) From an engineering perspective, the formal elements of Gil’s “Smoothed Lindbladian” models already are widely and successfully applied … and these applications will be the subject of Part II.
For Part II of “It All Turns on Naturality” — which surveys concrete realizations in varietal dynamical systems of the Kalai Conjectures — see (briefly) the above Quantum Pontiff comments or at greater length our Soldier Healing Seminar’s “Green Sheet” notes for 2013.
Please let me express (again) my profound appreciation and sincere thanks — without regard differences of opinion, and especially on behalf of medical researchers — to all who have participated so creatively in the Kalai/Harrow discourse.
This thanks is extended particularly to Aram Harrow, Gil Kalai, Steve Flammia, Dave Bacon, John Preskill, Scott Aaronson, Dick Liption, Ken Regan, and anyone else whose name(s) should have occurred to me. Thank you all!
As a supplement to Part II, there is now a brief historical survey Alexander Grothendieck’s enigmatic-yet-celebrated question (celebrated among mathematicians and historians anyway) “What is a meter?“
Gil,
Thanks for this unexpected publicity!
I’d like to clarify/follow up on my earlier remarks about topological quantum computation (TQC) with nonabelian anyons. The concern was that, while it seems we both agree that time evolution of well-separated anyons should be inherently robust against on-going errors (because coupling to the environment is through local operators only), the initialization step for the anyons would involve them not being well-separated for a short time, and during that time they would be potentially vulnerable to errors. Then time evolution of such faulty initial states would of course give poor results. Then it may seem that TQC would not have intrinsic fault tolerance, and would be no better in principle than ordinary QC methods using qubits and gates. I’ll admit to worrying over this briefly.
But there are also methods for preparing the initial state of nonabelions that are themselves protected against errors in principle. Usually, these involve measurements. Suppose for example
that we use the popular model, and so a pair of nonabelions has two states which I will call 0 and 1. For computation we want all pairs to be 0 initially. After creating pairs of these anyons, we make the members of each pair well-separated, so now we agree that, whatever their state is (a superposition of 0 and 1), it is robust against errors. Then we make a measurement on each pair, with result 0 or 1 for each. This can be done by passing further nonabelions around a pair, far away, and using interferometry, and is again robust against errors (indeed, the measurement can be done repeatedly as a check.) This projects each pair to either 0 or 1. Then even if there is some chance that during preparation of a pair we get 1 instead of 0 with some frequency, we can use more pairs than we need for computation, and discard the ones in the 1 state so that we have enough 0s for our computation. This can be done with error as small as you wish and only polynomial time overhead. (Thanks to Steve Simon for help with this argument; Steve is one of the authors of the review cited by Gil above, where more information about these kinds of measurements can be obtained.)
So you see that there is much more here that you will need to explain away in order to refute the mere possibility of TQC!
Nick
Dear Nick,
Many thanks for your comment. It is great to host you on my blog, and in accordance with my policy that every bit of reputation gained on my blog (e.g. by participation of famous people) will be wasted here too, your comment means that, like in similar cases, I will have to share the readers with an entertaining yet embarrassing story (like this one or this one or this one or this one) or something like that.
I will think more about your comment before referring to details (and I think I owe answers to a few points you raised in Scott’s blog). Let me just mention now that my main objective is not to refute the mere possibility of QC or TQC, but to offer the absence of quantum fault-tolerance as a powerful tool to explain our (quantum) reality.
“… my main objective is not to refute the mere possibility of QC or TQC, but to offer the absence of quantum fault-tolerance as a powerful tool to explain our (quantum) reality.” Is it likely that nature has an absence of quantum fault-tolerance if and only if Bell’s theorem is false? Who might be some of the main physicists who believe that Bell’s theorem is false? Have there been any collaborations between students of Gerard ‘t Hooft and students of Gil Kalai?
Nick,
“So you see that there is much more here that you will need to explain away in order to refute the mere possibility of TQC!”
This is what I wrote in the last post of our debate on this matter:
So, as you can see from this quote, I agree that there is much more to be explained. I may have some reservations regarding what “you” should mean. The way I see it it should mainly apply to the TQC people themselves – they should be the chief skeptics of the endeavor.
My argument, in general is this: you look on the one side at the experimental process you propose for creating your anyonic qubits and performing gates on them (this corresponds to “experimental miracles occur” in the pair of pictures above) and you also look at a (noisy) quantum computer that simulate your experimental process.
If you can achieve noiseless computation on the experimental side then you should be able to demonstrate it on the noisy computer side. If the evolution on the experimental side does not enact (the full complicated apparatus of) quantum fault-tolerance then you should be able to achieve noiseless quantum computation on the noisy computer side without the complicated process of quantum fault-tolerance as well.
This argument suggests that if you look at concrete proposed implementations of the Nayak et als paper you will discover that both the qubits involves mixtures of logical errors and the gates are imperfect so they involve mixture of the desired outcome with a cloud of logical errors. But, as I said in the debate, this is something yet to be elaborated for detailed specific implementations. Regarding Simons’ measurement-based “purifying” of anyonic qubits. This is a sort of simple form of (partial) quantum error-correction and I don’t see what is special about anyonic qubits in this proposal.
Gil
Gil,
Earlier you agreed that the evolution of well-separated nonabelions will not generate
errors (i.e. the gates are not imperfect), so you should be addressing the initialization question. The measurement-based purification is not error correction at all, but initialization. Of course it is used in other implementations (say with qubits). What is different here is that we use the phase picked up when a nonabelion passes around a pair
at some large distance, which you agreed is topologically protected. The phase is measured by interferometry and this can be made as reliable as one wishes, it seems.
As for your argument that it should be possible to simulate the whole thing on a noisy QC, and hence if the latter does not work, neither can the former: this seems still to be question begging (as both Scott and I said before). It is logically possible (that is, playing devil’s advocate) that the conventional noisy QC fails to work, and the TQC does work. If so it just shows that the TQC does a better job. (Then you should use the TQC in place of the other implementation when simulating a universal QC.) It’s also not clear why the success of the topological implementation (without any extra apparatus) means it must be possible to simulate it on a conventional QC without the need for error correction there either. The two are simply different. Of course, it is also possible that both work, and that you are wrong.
Obviously I’m not claiming that we (on the topological side) already know all about how to implement the concept in every detail; only that the original idea that initializing will necessarily be vulnerable to errors, and so will need additional fault tolerance/error correction, is not correct, at least not in the form in which it was envisioned.
Nick
Nick,
“It’s also not clear why the success of the topological implementation (without any extra apparatus) means it must be possible to simulate it on a conventional QC without the need for error correction there either.”
As I see it, indeed the essense of my argument (and all that is needed) is:
This looks correct to me and I will be happy to clarify it either on the abstract level or (but this will require more effort) by looking carefully at a specific implementation.
If (*) is correct then I expect that this implies that the computation with topological qubits and gates does not perform better than a computation with ordinary noisy qubits and gates without quantum fault-tolerance. (And, yes, this should apply to qubits and to gates.)
Gil
Dear Nick: Here is something that you wrote on Shtetl Optimized that I did not answer. In the heat of the discussion it was delayed, and your nonabelions took higher priority, so let me reply over here on this cozy blog. Of course, I amply talk about it the videos and in my debate with Aram but you are surely entitled to a personal answer and a fresh thought.
I did give several reasons to prefer my convoluted noise models over the possibility of quantum supremacy and quantum fault-tolerance. This is the beginning of “Part VII” of my talk in video 2 28:00-35:00. I also do not agree with the “not otherwise observed”- what we observe in nature is that approximations/noise respect internal structure and symmetries of the “signal” and this actually goes along with my point of view, and against the view of noise based on “computational basis.” I do agree with the “not otherwise expected” part. Right now Aram and I (talking with some colleagues) are trying to see what the standard Hamiltonian noise models tell us about the life-time and decay behavior of a single superconducting qubit. (Indeed Aram expects that Hamiltonian models like those of this paper by Preskill will give the correct picture, and I disagree.) I also did explain in several places why and how these “mysterious” correlated errors arise, and why they are less mysterious than it seems, e.g. Video 1 56:00 – untill the end.
As a matter of fact, not giving up the extended Church-Turing thesis was not on the top of my list (it is the last of seven items on my list) for my reasons to disbelive quantum computers. After so many years of hearing about quantum computing and post-classical computation and cryptography, I also felt a little blasé about it. So why not give up the extended Church-Turing thesis? Let me quote Seth Lloyd (as quoted in my overview):
What Seth says is absolutely correct and it is simply a more vivid way to say what giving up the extended Church-Turing hypothesis means.
Now, we do have non conventional weapons, but we cannot really expect a non conventional bomb with more power than a conventional bomb of the size of the entire universe, right? And we cannot hope for a machine with more horsepower than the number of horses that can be packed in the entire universe. When was the last time we witnessed human-made changes scaled like the accumulative impact of the entire universe? So, while not impossible, I do not think that giving up the extended Church-Turing thesis is something to be taken lightly. (In fact, I myself took it too lightly along the years.)
I can try answering this last objection of Gil’s. Let’s look at New London, CT and Orient Point, NY (on Long Island). Suppose you wanted to drive between them. Google Maps says that driving between them takes three hours and forty minutes, and the average speed is slightly faster than 50 miles an hour, probably somewhat unrealistic considering you have to drive by New York City. But there’s another way to get there! You could take the ferry. Since this only takes one hour and twenty minutes, it clearly goes 2.75 times as fast, so it must be going well over 130 miles per hour.
I’ve been on that ferry, and it sure didn’t seem we were going that fast.
I hope everybody reading this has seen the flaw in my reasoning.
But this is also the flaw in Gil Kalai’s reasoning—the difference between classical algorithms and quantum algorithms is that quantum algorithms take a different route to get to the answer—a route that is not accessible to classical computers. You don’t expect all classical algorithms to take the same number of steps to the solution—the number field sieve factors numbers much faster than trial division. Why do you believe that quantum algorithms, which take a different route, cannot solve some problems faster than classical problems?
Dear Peter,
Thanks, as always, for your comment.
Of course, we agree that a different route can lead to more power. In my comment, I gave the example of nuclear weapons where we gain five or six orders of magnitude compared to conventional explosives and you gave an example where we gain a factor of 2.75 by taking a ferry. My remark was that proposing a different route which makes a difference whose magnitude is correctly described by Seth in terms of the size of the entire universe, is more dramatic and hence less plausible and, while not impossible, should not be taken lightly at all.
We also share the belief that quantum algorithms can solve problems much faster than classical algorithms, but I expect that a realistic noise modeling does not support the abstract model of quantum algorithms. On the physics side the way I see it is as follows: there is an important concept of locality which is crucial in describing our quantum reality and comes on top of the very basic framework of QM. The crucial question regarding QC is how to model errors and approximations. The ordinary models impose locality on the errors and thus allow fantastic non local states to be achieved for the computation. My proposal is to have a noise model where locality emerges from the model itself both for the nature of errors and for the nature of the computational outcomes.
On a lighter note, I had a quantum-related experience similar to your Google-Maps story. I tried to invite Michel Devoret in person to QSTART and checked with Google Maps how to reach the address of his office from my office at Yale. Looking at the map itself I then realized that our offices are essentially in the same building which gave a different route with substantial speed-up compared to the Google Maps suggestion.
I admire greatly Michel and Rob Schoelkopf’s amazing progress on superconducting qubits (and other things) but I regard it implausible that their efforts will lead to a new route,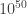
more powerful, for sampling permanents of a 50 x 100 matrix or for factoring 2000-digits integers. It is much more likely, in my opinion, that their work will be part of a new route for better understanding some aspects of quantum physics.
For the largest numbers factored on a conventional computer, the speed-up from trial division to number field sieve is already on the order of the computational power of the entire universe. So if you judge the quantum algorithm speed-up by algorithmic standards, it’s not that big. On the other hand, if you judge it by order-of-magnitude improvement of our control of physical phenomena, it’s enormous.
Dear Gil,
Your idea with limited horsepower sounds reasonable for me, but how it is related with fault tolerance? Let’s consider a thought experiment: someone has working quantum computer, but after factoring test the results are encoding using standard method with addition of random numbers. So nobody may use results (without knowledge of the random numbers), but we may not say that addition of the noise reduces power of the quantum computer itself.
Why the fault tolerance problems may not be considered as a similar example then Nature is working with huge horsepower, but we simply may not use or control that? So, I could suppose, that fault tolerance and limited horsepower idea (aka ECT?) are two different problems.
Dear Alexander, Your porposal: that nature works in much higher “horsepowers” that we simply cannot “use” or “control” (or even cannot give direct evidence to) seems implausible to me (but not impossible).
Gil, Sorry if I was unclear, but I wrote about different thing: it is not clear for me, how failure of quantum computing due to noise may restore ECT. It is even not proposal, I supposed that my thought experiment raised such suggestion in a status of some “lemma”.
Let me explain idea of my thought experiment better:
I have a system quantum computer + noise and so it not less power than quantum computer alone. So if quantum computer disprove ECT some *additional* effect may not restore that because for modeling of such system we must (1) model quantum computer (2) model the noise. I only need to add, that it is rather some intensification of ECT adapted for “horsepower” idea, because some weak (“dishonest”) version of ECT may accept in such a case model with noise without modeling previous process with claim that it is not possible to distinguish result without knowledge about noise. But such “dishonest” ECT may not work with horsepower idea, because in such a case for estimation of the horsepower you may model all processes.
Physically speaking, Hilbertism’s appreciation of TQC is substantially grounded in the (postulated) invariant reproducibility and unbounded accuracy of the quantum metrology triangle (QMT, a.k.a.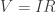
, with 
, 
, and 
measured independently), and in particular, on the topologically robust quantum coherence that is associated to both the measurement of 
(via the inverse AC Josephson Effect) and the measurement of 
(via the integer Quantum Hall Effect (IQHE) ).
There are at least three grounds for humility in regard to whether the QMT’s success (to date) assures the future success of TQC:
• Reflection I Our present understanding of noise mechanisms generally in QMTs, and particularly in the IQHE, is very far from comprehensive (e.g, per the Weiss and von Klitzing work cited below).
• Reflection II It is not presently known whether an entirely satisfactory simulation of QMTs in general (and IQHE measurement processes in particular), might perhaps achievable with PTIME computational resources, within the restricted domain of varietal dynamics (regarded as a formal model of the Kalai Postulates, and compatibly, a restriction of Hilbertism to Dirac-Maxwell dynamics).
• Reflection III Strenuous experimental efforts to observe nonabelian anyon dynamics have not succeeded to date, even for the simplest systems (i.e., one or two anyons, although to be sure, some tantalizing hints *are* seen).
——————
In light of these reflections, here is an engineer’s appreciation of the Kalai/Harrow debate (which henceforth is depersonalized by calling it the “Hilbertism/Arnol’dism” debate):
Hilbertism asserts “Quantum computing has left the Extended Church-Turing Thesis hanging by a fingernail”; and so we can confidently foresee that TQT (or similar advances in quantum computing) will “force Gil Kalai to admit that he was wrong.”
Arnol’dism asserts La marée étale (“the slack tide”) of 20th century Hilbert-space dynamics has already given way to a 21st century marée montante (“flood tide”) of varietal dynamics; first QMTs, and then TQTs — and eventually (we may hope) all of computational dynamics — are destined to be immersed in the rising tide of our ever-deepening mathematical understanding.
Note The name “Arnol’dism” is proposed, first, to honor Vladimir Arnol’d’s creative lifetime achievements, that spanned multiple domains of mathematics, physics, engineering (and even “Pushkinistics”), and second, to honor Arnol’d’s maxim “It is not shameful to be a mathematician but it is shameful to be only a mathematician.”
Arnol’d’s maxim directs our reflections toward …
Grothendieck’s Wager Supposing that decades from now (or even centuries from now) Hilbertism is proven to be entirely correct (e.g., by the experimental demonstration large-scale fully-programmable FTQCs), such that Arnol’dism is entirely discredited, then nonetheless it is rational to ardently embrace Arnol’dism’s marée montante — at least during the next few decades fo the 21st century — on the pragmatic grounds that an ever-hotter planet, with ten billion hominids upon it, can scarcely afford to deprecate the ever-improving Arnol’dian simulation technologies upon which the 21st century already relies to supply its marée montante of absolute requirements for food, clothing, shelter, and medical advances.
To say nothing of the already-urgent and ever-mounting need to create family-supporting jobs that supply these needs.
Conclusion Even if Hilbertism is true, our generation of mathematicians, engineers, and scientists is well-advised to embrace Arnol’dism wholeheartedly, so that la marée montante of our mathematical understanding — and in consequence la marée montante of our PTIME simulation capabilities — rises as high as feasible, and as fast as feasible, for as long as feasible.
Dear John, thanks for your comments. Overall I think that while it is useful to pose an alternative for the perception that QCs are possible it is premature to try to convince believers to change their mind and, in any case, there are experimental efforts that may shed light on the matter in the next years. Scott’s quote (2) refers to BosonSampling which is interesting but something of an offshoot of main QC anyway. For BosonSampling I do think that noise sensitivity gives a clear explanation for why realistic BosonSampling leads to a flat distribution (and is thus computationally trivial) and hence experimentally the observed distribution will have no correlation with the distribution expected by permanents when the number of bosons grows. Because of the strong noise-sensitivity effect I expect that this will be shown for a handful of bosons. So, on this matter I do expect Scott (and others believers in the possibility to use BosonSampling to support “quantum supremacy”) to change their minds in the months to come.
Update: (March 27) What we expect now (see this comment) is that the noisy distribution will not be flat but still bounded away from the expected distribution even when the noise is small.
I often explain it in terms of the difference between two multiplication algorithms.
One is the first one that kids learn (17 x 11 = 17 + 17 + … + 17), and the other is the O(n^2) one we learn a little later.
I agree that the failure of the ECT thesis is a little surprising. But I think it is _less_ surprising than Bell inequalities, the Aharonov-Bohm effect, the uncertainty principle and tunneling. These basic features of quantum mechanics are pretty uncontroversial. But once you accept that they are the building blocks of our world, fast factoring algorithms seem less outrageous.
See Leonid Levin’s comments here: https://groups.google.com/forum/m/#!msg/sci.physics.research/GE5cz3xefCc/e0eh34MZGdwJ
He nails it.
Prof. Kalai: ‘t Hooft claims that the one testable prediction of his theory of superstring determinism is that quantum computers won’t work well enough to be useful. Do you agree that ‘t Hooft’s theory really does make this prediction? Also I have attempted to convince string theorists of the following claim: The main problem with string theory is that string theorists fail to realize that Milgrom is the Kepler of contemporary cosmology. If Milgrom’s acceleration law is wrong, then what is the explanation for the flyby anomaly?
Does the Fernández-Rañada-Milgrom Effect Explain the Flyby Anomaly?
Is it likely that a quantum theory of gravity would imply that quantum computers won’t work?
Gil:
As I understand your “why topological quantum computers cannot work”, your argument is that topological quantum computers could be simulated in the gate model, and we know the gate model cannot work, so topological quantum computers cannot work.
It seems that this misses the point: anyons are a physical phenomenon, and you should address how the failure of quantum topological computation is reflected by the physical phenomenon of anyons. What does this mean for materials containing non-abelion anyons. It seems there are several possibilities. Some of these (I’m not giving an exhaustive list) are:
• anyons cannot actually exist.
• anyons do exist, but cannot have the properties (predicted by Chern-Simons theory) that they require for universal computation.
• anyons do exist, but interact with each other even when they are very far apart, and thus do not sustain quantum computation.
• anyons do exist, but any material that permits anyons must permit spontaneous pair creation of anyons at a rate incompatible with its use for quantum computation.
• anyons do exist, and they behave exactly as predicted by the physics theories except when you try to use them for quantum computation, and then mysterious errors arise which make the quantum computation fail.
The progress on creating anyonic materials is proceeding at a rate that within a decade or so I expect people may be able to control these materials reasonably well. If you want physicists to believe you have a real theory, you should predict exactly which of these possibilities is the way in which topological quantum computation will fail.
Hi Peter,
Not quite, but let me rephrase my argument using your wording:
I would word it as follows:
.. topological quantum computers could be simulated in the gate model, and we know that the gate model cannot work without the quantum fault-tolerance apparatus, so topological quantum computers cannot work.”
The argument is more specific than that: we have a picture on what will happen for a quantum computer with the qubit/gate architecture when quantum fault-tolerance is not applied and errors accumulate. For example, when you create a quantum error-correcting code there will be a substantial amount of logical errors.
Now, suppose that (1) you have a quantum computer which does not apply quantum fault-tolerance, (2) you have a quantum algorithm that creates a surface code, and (3) you succeed to lower the qubit/gate noise so that the target state will be close enough to the intended state. Then the state you will achieve is a mixed-cloud of codewords around the intended codeword (in addition to some errors in the computational basis.)
So what I say is that the experimental process to create an anyonic qubit will behave just like a quantum algorithm that you run on such a quantum computer.
Again, the crucial point is not that this qubit/gate computer cannot work, but that (without quantum fault-tolerance) when such a qubit/gate computer does work we can tell what will be the nature of quantum states it gives.
Lets see if we can agree on this point and then I will be happy to think about the further points that you have raised.
Hi Gil,
The quantum state of any material which allows anyons is already a quantum error-correcting code, so there’s no reason we shouldn’t be able to use the gate model without fault-tolerance to simulate this. I suppose initializing the quantum state of the anyons might be a problem, but Nick has already explained how to do that.
Hi Peter, Just before we move to “the material that allows anyons”, is my argument above clearer?
“The quantum state of any material which allows anyons is already a quantum error-correcting code,”
I am not sure what precisely you mean by the “material which allows anyons.” .
In any case, for me when you talk about “a quantum error-correcting code” the main question is how does a non-zero entropy element in this “quantum error-correcting code” behave.
Do we have:
A) a mixture of codewords or
B) a delta function in the Hilbert space of codewords
(both perhaps + some “local noise”)
“I suppose initializing the quantum state of the anyons might be a problem, but Nick has already explained how to do that.”
The argument that I outlined above suggests that in any way you go about it in your laboratory you will get noisy quantum error correcting codes of type A (and not of type B). This does not apply just to “initialization” but also to any intermediate state. So it will apply also to an attempt to experimentally implement Nick’s suggestion.
Hi Gil,
The two options you are giving me are completely inadequate to choose between.
Of course, we will always get a mixture of codewords. The question is, can we reduce this mixture so it occupies an exponentially small volume with polynomial overhead? That’s the point of quantum error correction.
Peter, I should have made myself clearer (this is something I repeat again and again in my lectures). When I say “mixture” I mean that there will be a substantial mixture of logical errors. My entire point is that you cannot substantially improve the quality of “logical qubits” compared to the “physical qubits” this is what you cannot do with a noisy quantum computer without the quantum fault tolerance apparatus and this is what I expect you cannot do also in “ordinary” experimental processes that do not involve quantum fault-tolerance.
[Again, if the logical errors are negligible for me it is option B.]
Hi Gil,
For topological quantum computation, the idea is that you can improve the ratio of logical qubits to physical qubits by (1) doing a better job of initialization and (2) by keeping the anyons further apart.
The reason that this doesn’t introduce any paradoxes when you simulate it in the quantum gate model is that Hamiltonians that give rise to anyons have quantum fault-tolerant codes hidden inside of them.
This request for clarification — asked of a first-rank physicist by a first-rank mathematician — calls to mind Vladimir Arnol’d’s lament “Every mathematician knows that it is impossible to understand any elementary course in thermodynamics.”
Similarly, from a mathematician’s point-of-view — and equivalently, from a computational simulationist’s point-of-view — what is “impossible to understand” about anyonic dynamics is *NOT* the topologically protected dynamical phases that are associated to braided trajectories of anyons, but rather, the mechanisms by which coarse-grained anyonic dynamics (by postulate) arises from fine-grained Maxwell-Dirac dynamics, and is (postulated to be) robust in respect to the renormalization dynamics associated to edges, sensors, defects, and vacuua.
Survey articles like Elliot Lieb’s “Quantum Mechanics, the Stability of Matter and Quantum Electrodynamics” (2004, arXiv:math-ph/0401004) can assist mathematicians toward an appreciation that
These considerations remind us that the restriction of quantum dynamics to QED flows can be problematical for mathematicians and experimentalists alike.
In particular, QED dynamics compels us accept renormalization effects and long-range large-
gauge interactions — as manifest in flux tubes & image charges, for example — that can be severely problematic for quantum computation (as the experience of recent years has taught us). On the other hand, these same QED effects act generically to ease the task of PTIME simulation. Evidently the QED-restricted gauge-invariant long-range quantum dynamics that Nature imposes upon us has very special properties, that can either hurt us or help us, depending upon how we exploit them.
The wonderful articles of the Royal Society’s recent theme issue “The New SI Based on Fundamental Constants” (Phil. Trans. R. Soc. A, October 28, 2011; 369 (1953)) can be read, with a mathematical eye, as the physics embodiment of André Weil’s paean (written to his sister, the philosopher Simone Weil)
Similarly, the Royal Society’s various “New SI” articles show us that in regard to abelian anyonic dynamics
A great open question is: Can God similarly carry the day in regard to nonabelian anyon dynamics, against a devil who restricts human technologies (and human physiologies) to QED dynamical flows? For example, are topologically protected QED-restricted nonabelian anyonic quantum memories feasible, both in principle and in practice?
No one knows … and our present understanding is too feeble (as it seems to me) to foresee the answer with any great confidence.
One reasonable step toward resolving these questions — a step that is has not as yet been taken — is to mathematically naturalize the experimentally robust mises en pratique of present-day QED-restricted abelian metrology triangles, with a practical view toward similarly naturalizing the (hopefully robust?) mises en pratique of future QED-restricted nonabelian metrology triangles.
Conclusion There’s plenty of scope for Peter Shor and Gil Kalai to work together in advancing our present far-from-complete and far-from-natural understanding of anyonic dynamics, both abelian and nonabelian.
Needless to say, as a medical researcher I have a vested interested in ever-more-natural mathematical understanding of quantum dynamical systems, and ever-more-efficient simulation of them, and ever-more-robust mises en pratique for observing-and-controlling such systems. This is because we can confidently anticipate that the 21st century’s transformational advances in quantum information theory and quantum computing will be accompanied by transformational advances in medical technology and healing. So let’s keep advancing!
Gil,
How exactly do you get around my argument for initializing the state of the nonabelions?
I thought you had agreed that the braiding of well-separated nonabelions gives unitary operations that are topologically protected against errors (up to overall phases, anyway). You seem to have changed your mind about that, and are relying on your hypothesis (*) in a reply above, which as far as I am concerned is a non-argument.
Nick
Dear Nick,
The crux of the matter is the argument or non-argument (*). It is commonly accepted that quantum experimental processes that you run in the laboratory can be simulated on a qubit/gate quantum computer. Namely, you can describe your process by local quantum operations on some microscopic components describing your experiment. The extra ingredient for (*) is that if your experimental process itself does not involve an apparatus of quantum fault-tolerance (on the microscopic level that you use for its simulation) then you can imitate it (by tuning also the level of noise to fit the experiment) on the noisy quantum computer as well.
This is it.I think it is a good argument. I realize that you regard it as a non-argument. If you can say anything more that enlighten me I will be quite happy and will gladly change my mind if required.
(Regarding our discussion – actually, in this case I did not change my mind. I thought that you agree that TQC qubits cannot be initialized based on (*) and I parenthetically remarked that you cannot run a [unitary] quantum computation on (logically)-noisy qubits *EVEN* if your gates are noiseless. (*) as good as it may or may not be, applies to creating highly stable qubits, initially or anytime later)
Hi Gil:
If your gates are noiseless but you start with moderately noisy qubits, but not ones in a completely mixed state, you can indeed do quantum computation. You can run a unitary quantum computation that refrigerates a portion of your qubits at the cost of making the rest very noisy. You can then run your computation on the cold section of your qubits.
So if you can do everything noise free except initialization, this shouldn’t be an obstacle to quantum computers.
Gil:
Re our discussion—I never agreed to anything based on your (*) argument or similar. I thought I had explained that you can indeed initialize the nonabelion “qubits” in a fault-tolerant manner. (I agreed, and agree, that if you have faulty initial qubits, then even noiseless gates won’t help you.)
As far as I am concerned, simulating your experiment on any kind of other quantum device is beside the point. The question is what you can do in the actual device at hand. There is very little point in simulating the computation done by my perfect topological gates in a faulty non-topological quantum circuit. If it doesn’t work in the simulation, that tells us nothing about the original topological device. That is why your argument has always appeared to be begging the question.
Of course, if by “simulate” you mean constructing the topological phase in another system (perhaps in terms of qubits), possibly with a different (but still short-range) Hamiltonian but with a ground state in the same phase, then such a set-up should be just as fault tolerant as the original. (Indeed, people discuss exactly this a lot nowadays, with reference to cold atoms in optical lattices.) But in this point of view, either realization is as good as the other, so again I don’t see what you have learned from the “simulation” that you could not in principle have seen in the original.
In a way the point here is that when we say the TQC is inherently fault tolerant, we are not kidding. We mean that notwithstanding the coupling of e.g. charged electrons to the electromagnetic environment as in the fractional QH effect—so our systems do already contain “noise”—the topological degrees of freedom are stable against decoherence, and fault-tolerant gate operations and initialization are possible, up to exponentially-small corrections.
Dear Nick, I suppose we simply disagree. Perhaps the only point of agreement is when you say “either realization is as good as the other” as indeed the same weakness with TQC applies to other attempts to implement stable qubits based on topological phase that shortcut the bottom-up tedious quantum fault-tolerance approaches. Such shortcuts involve some extra miracle which represents not-sufficiently-detailed modeling of the noisy processes. Your systems do contain “noise” but not the “whole noise” (which will leave you with “nothing but noise”).
Gil,
Please just tell us how errors can occur when we braid well-separated nonabelions adiabatically.
Nick
Nick, as you see from the top of this comment this question is on my mind and I will certainly try to come back to it (but probably not in real-time). In the meantime, here is one to you:
How low-quality should the anyonic qubits be to start with before your belief in noiseless braiding gates will shatter (and why). Or is it the case that the slightest sign of an
anyonic behavior that deviates from a maximal entropy state will suffice to manifest the wonderful noiseless braided gate phenomenon (and thus to apply your purification argument).
Hi Gil,
The refrigeration algorithm works as long as (1) the gates are noiseless and (2) the initial state is not completely mixed. You just need more qubits to start with to produce the same number of working qubits after cooling.
There’s a nice classical explanation for this. Suppose we start with n. Process them three bits at a time. Do a reversible computation that puts the majority of the three bits in the first bit, and encodes which bit is different in the remaining 2. If the bits started out i.i.d. with a bias toward 0, the entropy of the first bit has decreased, and the entropy of the other 2 has increased. Repeat, segregating the lower-entropy bits from the higher-entropy bits. Eventually, you will get nearly all your entropy in the last k bits, and have the first n−k bits nearly all 0.
Gil, I’ll take the last question first. We’re talking about initializing a set of “topological qubits” so that we have all 0’s. (I think Peter is talking about error-correction during the computation, a different question.) I’m not sure what entropy you mean. My previous discussion was for a state that was pure but in a superposition. If you want to start with a mixed state (density matrix), we can do that also. In fact, you can take the density matrix of maximum von Neumann entropy, which is the equal weight statistical mixture of all the basis states (bit strings). Then it is easy to see that measuring each topo qubit, we will find about 50% in the 0 state, with \sqrt{N} fluctuations (for N topo qubits). So if you want some number M of qubits in 0 state initially, you would need to start with a little more than 2M qubits in this case.
To “shatter my belief” in noiseless gates you would need to demonstrate that the braiding of two nonabelions does not produce the ideal unitary asymptotically, up to corrections (or error rates) that are exponentially small in a) separation, b) 1/speed of braid, and c) 1/temperature, in the limit as all these quantities go to infinity. If you have braiding obeying the latter properties, you can do both initialization and computation.
Nick
Hi Nick,
No, I’m talking about the same problem as you are: initialization. I’m just trying to explain a different way of doing it (computational refrigeration).
Peter, thanks, yes, I see now. I had basically overlooked one of your posts dated March 31.
Peter,
Perhaps for improving that ratio you should also have added (3) exchange the anyons more slowly.
Dear Nick and Peter, thanks for your many enlightening comments. I will relate to some of your points a bit later. Thanks also Craig, David and Aram.
Dear Nick and Peter,
1) Peter: “The progress on creating anyonic materials is proceeding at a rate that within a decade or so I expect people may be able to control these materials reasonably well.”
Certainly this is a project worth pursuing. When we talk about gates/qubits with full fledged quantum fault-tolerance the difficulties in controlling the system are modeled in the basic noise/errors models. (And the debate is about the modeling.) For proposals to shortcut the traditional qubit/gates or parts of it, the “ability to control” is not part of the modeling. This is why I consider such “shortcuts” proposals as depending more on some “hidden miracle.” Difficulties in the “ability to control” may reflect engineering issues as well as basic physical obstacles.
2) My simulation argument asserts that if you have such a shortcut you should be able to demonstrate the detailed/microscopic description of your experimental process on a noisy quantum computer without quantum fault-tolerance. This suggests that a detailed modeling on the proposed experimental process (even with ordinary modeling of noise) may be in conflict with the experimental hopes. But, of course, the argument does not replace the need for such a detailed modeling.
Here are Nick’s and Peter’s responses.
Nick: “As far as I am concerned, simulating your experiment on any kind of other quantum device is beside the point. The question is what you can do in the actual device at hand. There is very little point in simulating the computation done by my perfect topological gates in a faulty non-topological quantum circuit. If it doesn’t work in the simulation, that tells us nothing about the original topological device. That is why your argument has always appeared to be begging the question.”
Peter: “The reason that this doesn’t introduce any paradoxes when you simulate it in the quantum gate model is that Hamiltonians that give rise to anyons have quantum fault-tolerant codes hidden inside of them.”
I don’t agree with Nick that this is beside the point. What Peter says is not impossible but seems implausible. The simulation argument suggests that creating Hamiltonian with hidden quantum fault-tolerance already requires quantum fault-tolerance on some finer level. I cannot exclude the possibility of some natural hidden quantum fault-tolerance resource but it looks unlikely.
3) Nick: “To “shatter my belief” in noiseless gates you would need to demonstrate that the braiding of two nonabelions does not produce the ideal unitary asymptotically, up to corrections (or error rates) that are exponentially small in a) separation, b) 1/speed of braid, and c) 1/temperature, in the limit as all these quantities go to infinity. If you have braiding obeying the latter properties, you can do both initialization and computation.”
Nick, what you describe is more or less a “threshold-like theorem,” which I have no reasons to disagree with. The basic alternative to the threshold-theorem view of the quantum world is simply that the rate of noise scales up for complicated quantum evolutions. Also here, the alternative is simply that you cannot achieve the requirements that you listed for noiseless braid-based gates. (Reminder: for me noiseless= exponentially small noise.)
4) Initialization: A demonstration of (almost) noiseless qubit at a presecibed superposition would mean crossing the “fault-tolerance barrier,” and thus the failure of my conjectures. The nice refrigiration argument of Nick and Steve indeed asserts that with noiseless gates and noiseless measurements you can start with anyonic qubit with arbitrary small deviation from the maximal entropy state and refrigirate it to a qubit at a (almost) pure presecribed state. If you are seriously not kidding about this, Nick, I think it is up to you to look here skeptically and examine if for realistic implementations we have a case of unrealistic assumptions begging an unrealistic conclusion.
5) It is certainly an exciting possibility that nonabelions cannot be constructed at all but it goes beyond the assertion that anyonic qubits cannot be better than other types of qubits. (This question is related to the second part of my talk in the TQC video.) Impossibility of “deep” quantum computation (or even if deep quantum processes are not witnessed in, say, condensed matter physics,) would imply strong conservation laws for topological phases and may support such a possibility.
I cannot help but feel that this line “the rate of noise scales up for complicated quantum evolutions” is attempting to present an alternative as simple when it is really anything but. How does the system know its evolution is complicated? What does complicated mean? Calling this alternative “basic” seems to me crazy when still no one can write down a local Hamiltonian that generates it.
Dear Aram,
I cannot help but feel that this line “the rate of noise scales up for complicated quantum evolutions” is attempting to present an alternative as simple when it is really anything but.
Aram, the bottom line is simple, fortunately there is more to be said.
How does the system know its evolution is complicated?
This question reflects what I refer to as the “trivial flaw.” The question takes for granted a reality with quantum computers and a causality structure of universal quantum devices. In our present reality a system is built to carry out an evolution (or a class of evolutions), the errors and risks depend on the quantum device, and the device depends on the evolution.
What does complicated mean?
This is, of course, a good question and the answer is more involved than the very simple bottom line that you quoted. For systems attempting to implement qubits/gates quantum computers “complicated” can be thought of as “very entangled” in certain technical terms that can be found in my papers.
Calling this alternative “basic” seems to me crazy when still no one can write down a local Hamiltonian that generates it.
This represents another “blind spot” in your perception, Aram. You expect an explicit description in term of local Hamiltonians and I expect (and largely propose) implicit description in terms of conditions connecting the evolution and the noise. (Or, in other words, implicit conditions for the noisy perturbations of unitary evolutions.)
Ultimately, for noisy quantum systems that obeys my implicit conditions the noise can be described in terms of local Hamiltonians and there will be severe locality conditions also on the evolution itself. But note that my implicit conditions extend even to cases where “locality” has no meaning.
Implicit mathematical descriptions in terms of conditions or equations are very basic in mathematical modeling. (This last issue is similar to those I had with Scott Aaronson on the matter of “Navier-Stokes computers”, see this remark and this one.)
If you are interested and have some time, watch the videotaped lectures!
I guess we’ve been over some of this ground before, but controllable systems are usually capable of both complicated & simple evolutions. Do such systems experience unusually correlated noise for both types, or only in the complicated case? Either answer seems to lead to paradox.
It is true that I have a blind spot in that I am unable to understand your noise models apart from their conclusions (QCs don’t work). But are there any physicists who understand your noise models? Even ones who may agree with your conclusions, like Alicki, presumably get there in different ways.
Maybe what I am missing is that the conclusion “QC don’t work” is in fact the only premise? And the rest of your work is trying to explore the consequences of that?
“Maybe what I am missing is that the conclusion “QC don’t work” is in fact the only premise? And the rest of your work is trying to explore the consequences of that?” Dear Aram, to a large extent this is correct – see Video I 0:05-1:05 and Video II 1:01:50-1:03:44.My purpose is to offer an explanation for why quantum computers cannot work and drawing consequences from failure (or just absence) of quantum fault-tolerance is a large part of what I am doing. (When it comes to methods to shortcut fully or partially quantum fault-tolerance, there are stronger arguments for why they will not work.)
So if “quantum computers cannot work” is the premise of your theory, does your theory lead to any concrete predictions besides “quantum computers cannot work”? If it doesn’t, then I can’t help thinking that there really isn’t much substance to it.
The Kalai postulates, as formally modeled by varietal dynamics have led to concrete experiments, a concrete PhD thesis (coming this summer), concrete patent applications, and (most recently, and most gratifyingly) a concrete tenure-track faculty appointment for Joe Garbini and my graduate student Rio Picone … with no post-doc required.
These are four concrete reasons why we “varietal engineers” have evolved considerable (and increasing) respect for the Kalai Postulates.
John, I agree that varietal dynamics are a powerful and useful simulation tool, but I have to point out that they are not what Gil is proposing. One thing that Gil is clear about is that he wants his conjectures to be compatible with the (conventional) Schrodinger equation.
Aram, for us engineers there is no operational difference between:
• Varietal dynamics that “blows up” to QED field theory, versus
• QED field theory that “pulls back” to varietal dynamics.
The former accepts a dynamical restriction, namely, “Quantum computing Hamiltonians are required to respect Maxwell-Dirac relativistic gauge invariance.” The latter accepts a geometric restriction, namely “The singularities of varietal state-spaces must be computationally and thermodynamically occult.”
It is entirely reasonable (as it seems to me) to suppose that the dynamical restriction is dual to the geometric restriction, i.e. they are the *same* restriction.
From this dual perspective, it is natural to regard the “M” in Ed Witten’s celebrated M-theory as standing for what the Green Sheet seminar notes call mises en pratique in engineering roles, as dual to la marée montante in math-and-physics roles.
Here we can scarcely go wrong (as it seems to me) by following Grothendieck’s advice to Ronnie Brown:
Following Grothendieck’s advice, it is natural to pullback Gil Kalai’s postulates onto concrete conjectures like:
One nice aspect of this conjecture is that it respects the spirit of the Kalai Postulates (and even formally models them) without tackling divisive articles of faith regarding “The Church of the Larger Hilbert Space.” Instead, this conjecture directs our attention toward innumerable wonderful articles, ranging from Weis and von Klitzing’s ultra-concrete “Metrology and microscopic picture of the integer quantum Hall effect” (2011) to Herwig Hauser’s ultra-abstract “The Hironaka theorem on resolution of singularities (or: a proof we always wanted to understand)” (2002).
The main advantage that pretty much any modern-day researcher possesses — relative to ultra-talented 20th century polymaths like (e.g.) Paul Dirac and John von Neumann — is that we can draw from a pool of math-and-physics literature that is wider and deeper than Dirac and von Neumann ever dreamed of. And so (as it seems to me) the more deeply we all draw from this pool, the more effectively Kalai/Harrow debate can fulfull its immense and even strategically and morally crucial potential.
Doh! The second paragraph of the above comment transposed “former” and “latter”.
The main point is evident (I hope): the Kalai Postulates can be concretely reduced to Standard Dynamical Conjecture(s), that offer a path toward — that dangerous article — a reasoned, respectful consensus shared by Kalaists and the Harrowites, accompanied by a vigorous flow of creative research and productive enterprises. One hopes so, anyway!
Hi Peter (and Aram and John)
Thanks, all, for the comments.
Peter, the premise of my theory is that quantum fault-tolerance is not possible. (And, in any case, that “the fault-tolerance barrier” between quantum systems with quantum fault-tolerance and quantum system without quantum fault-tolerance is an important “phase transition” that deserved to be studied.) So, for me, the crux of the matter is quantum fault-tolerance/quantum error-correction and not quantum computing. Certainly I am not shy at all to make concrete, non-concrete, and vague predictions based on this premise and to offer various connections, applications, and speculations based on it. I am a bit off-line these days due to our Passover holiday but I will try to gather some of these predictions and post them later. I certainly think that “no quantum-fault-tolerance” is by itself an important principle related to many important issues. (Of course, it is a fairly common skeptical view that attempts to build quantum computers will fail but we will not learn anything new from it. I disagree and refer to this point for a few minutes in Video II from 12:17.)
Three remarks for now:
1) Some of the substance of my point of view comes from very simple claims based on a very simple logic
Often people think that this claim represents some unlikely conspiracy because they make the mistake of taking for granted the causality structure imposed by quantum computers. (This leads to the question that Aram asked here in the thread “how does the system ‘knows’ that the evolution is complicated.”)
Often, people require that my conjectures should be supported by an explicit ” ‘microscopic’ model of noise,” while I find implicit mathematical conditions perfectly adequate.
These two claims represent very simple logic. Still, while they do not involve cuspidal representations or derived functors, to the best of my judgement, there is substance to these claims even if they were incorrect. (But they are both correct.) In any case, I find it interesting to discuss them.
2) If quantum fault-tolerance is impossible (or when quantum fault-tolerance is absent for whatever reason) then I would expect that efficient classical approximations are possible. I did not study specifically the connections between varietal dynamics that John (and Aram) discussed and my conjectures/point of view, but this can certainly be very interesting.
3) A slogan (and an analogy) which describe my point of view is that “the importance of quantum fault-tolerance to physics is similar to the importance of nondeterministic computation in the theory of computation – their importance is that they cannot be achieved.” As thought experiments 1) What would be your predictions based on a principle of “no quantum fault-tolerance?” 2) Consider a hypothetical scenario where for a few decades people were trying to find efficient algorithms for NP-complete problems believing that this is possible. What could be then the additional predictions coming from a point of view that this is simply impossible.
Hi Gil,
Let me try to explain what I mean when I say your theory doesn’t make any predictions.
It seems to me that anyons lead to fault-tolerant quantum computation easily enough that the impossibility of fault-tolerant quantum computation must mean that anyonic materials behave very differently from what quantum mechanics predicts.
However, your thinking seems to be that anyonic materials might work exactly the same as quantum mechanics predicts they will, except for the fact that, if anybody actually manages to control the anyons well enough to do quantum computation, the computation will fail for mysterious reasons.
So the only thing that you are predicting from the assumption of no fault-tolerant quantum computation is that quantum computation won’t work.
Hi Peter,
Thanks for the good comment. Your comment consists of a paragraph on your view and continues with a few sentences on my thinking. Let me respond in two stages. First let me rephrase what you wrote for the bosonic case (which I studied in more details), and then I will move back to anyons.
The bosonic analog
(A’) It seems to me that bosons lead easily enough to BosonSampling which demonstrates “quantum supremacy, ” so the impossibility of (computationally superior) BosonSampling must mean that bosonic materials behave very differently from what quantum mechanics predicts.
Yes, realistic (noisy) bosonic states behave very differently from what quantum mechanics predicts for noiseless bosonic states.
(B’) However, your thinking seems to be that bosonic materials might work exactly the same as quantum mechanics predicts they will, except for the fact that, if anybody actually manages to control the bosons well enough to demonstrate (superior) quantum computation, the computation will fail for mysterious reasons.
I will rephrase the “my thinking” part in a stronger and simpler way as follows:
(C’) Nobody (nature included) can control bosonic states “well enough” to demonstrate superior quantum computation.
For the bosonic case (more precisely for states based on random gaussian matrices) I am working out the situation with Guy Kindler and our work suggests the following more concrete predictions.
(P’1) [noise-sensitivity] Even for small amount of noise in the creation process of the bosonic state there will be a very large difference (in terms of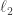
-norm) in the behavior of the ideal bosonic state and the noisy bosonic state.
(P’2) [small support] Realistic (noisy) bosonic states are supported by low degree Hermite-polynomials.
(P’2) means that for a fixed amount of noise the noisy versions have polynomial-time approximation.
Back to anyons
(A) “It seems to me that anyons lead to fault-tolerant quantum computation easily enough that the impossibility of fault-tolerant quantum computation must mean that anyonic materials behave very differently from what quantum mechanics predicts.”
Yes, like in the case of bosonic states small amount of noise in the process leading to “anyonic materials” will cause them to behave very differently than the ideal model. Both these behaviors are consistent with “what quantum mechanics predicts.”
(B) However, your thinking seems to be that anyonic materials might work exactly the same as quantum mechanics predicts they will, except for the fact that, if anybody actually manages to control the anyons well enough to do quantum computation, the computation will fail for mysterious reasons.
My thinking is that
(C) Nobody (nature included) can “control” the anyons well enough to demonstrate quantum-fault tolerance and do quantum computing.
((C) is both stronger and clearer than (B).)
Of course, you may ask, why don’t I have as concrete predictions for the anyonic case as I have for the bosonic case. I can make a few excuses: the mathematics and physics are deeper and more complicated. The implementation is more mysterious, for example, I am not sure what precisely you refer to as “anyonic materials.” Is it a hypothetical theoretical gadget, Peter, or do you refer really to some materials? Do you regard the implementation of surface code based on superconducting qubits an “anyonic material?” And finally, I simply did not study the anyonic case in detail.
We can expect to have predictions which are similar to (P’1) and (P’2) in the bosonic case, namely:
(P1) [Noise-sensitivity] Small amount of noise in the creation process of anyonic states leads to very large difference between the noisy states and the ideal states.
(P2) [Low-degree support] Realistic noisy anyonic states are supported by “low degree” representations and have polynomial-time approximations.
But unlike the bosonic state I do not have results supporting these predictions, and frankly I don’t understand the representation theory well enough to state (P2) in precise mathematical terms, so this is left to be explored.
As I said earlier, the simulation heuristic (which I regard as strong while not ironclad) applies both to anyonic and bosonic computation. (The application for anyons is stronger and more direct.) The simulation heuristics gives a clear prediction that anyonic-based qubits are noisy.
It is instructive and fun (and perhaps even practically useful) to consider restrictions of the above two statements, as follows:
The point is that it may not be neither computationally necessary, nor computationally feasible, nor even computationally desirable to embrace the goals that some crusaders advocate:
Rather, it may be preferable — in regard to advancing mathematics, science, engineering (and even medicine) — to instead progressively raise tide of RKC science to submerge the most lustrous crown jewels of quantum physics, that is: (1) abelian quantum metrology triangles of invariant reproducibility and unbounded precision, followed by (2) nonabelian metrology triangles, also of invariant reproducibility and unbounded precision.
Relative to the 2003-4 QIST Roadmap — which regrettably has neither been peer-assessed nor updated — the RKC/RKP dessein du marée montee is (as it seems to me) more mathematically natural, more experimentally verifiable, of greater engineering consequence, more stimulating of enterprise, more feasible in scope, more incremental in execution, more readily initiated, more objectively assessable, more respectful of urgent strategic and humanitarian requirements, more compatible with international agreements of long standing, and (most important of all) more inspirational to young researchers.
Needless to say, in this regard it is neither necessary, nor feasible, nor desirable that everyone think alike. Indeed the RKC/RKP dessein du marée montee already is well-underway, and is immersing quantum physics in a rising global appreciation that the Kalai Postulates, for at least the next few decades, may pragmatically be regarded as being effectively correct.
Grammatical Note The mavens of the French Language StackExchange aver that if the meaning to be conveyed is the English-language noun-phrase “a rising tide of mathematical understanding, regarded as a formalized research programme”, and the starting French-language phrase is Serre’s “méthode ‘marée montante'”, that concluded Serre’s celebrated (among mathematicians) correspondence with Grothendieck, then an appropriate French idiom is “dessein de la marée montante“.
In the language of Serre and Grothendieck, the QIST Roadmap can be appreciated as le dessein du marteau et du burin (“the programme of the hammer and chisel”), whereas RKC/RKP varietal dynamics can be appreciated as le dessein de la marée montante (“the programme of the rising varietal tide”),
Needless to say, in quantum information theory as in algebraic geometry, it’s reasonable to purse both approaches, as history shows us plainly, and common sense affirms, that each strengthens the other.
Hi Peter and John,
I have two additional remarks. First, Peter, it is not the case that my predictions (conjectures) come to play just when somebody tries to have quantum computing. In fact, I make an effort to offer predictions that can be tested well before we reach the stage of quantum computers, e.g., predictions for two (physical) qubits and for a single (encoded) qubit as well as predictions that apply to much more general quantum systems without even the tensor product structure. (There is an issue that I do not specify the constants and that some of the predictions are formulated in an asymptotic manner. I expect that the constants will be such that the predictions will come to play for quite small systems.) For anyons my prediction is simply that the mass gap allowing quantum computation cannot be approached. In the related attempts to create very stable qubits based on surface code, I mentioned various times that I expect that my conjectures will come into play in a substantial way already for the proposal for distance-3 codes involving 20 qubits or so. (This may be examined even via detailed simulations.) My prediction is that we cannot create up to small errors encoded qubits (where “qubit” refers to an encoded state with an arbitrary prescribed superposition).
As a matter of fact, some of my conjectures and, in particular, the issue of correlated errors for entangled qubits (which I am sure people are interested in, anyhow) can be tested already for the breakthrough experiments with just five qubits by Martinis at als reported in this paper: (Again, both for the real experimental level and the detailed simulation level). What is needed is to understand the probabilities of simultaneous k-qubits failures for sets of k-qubits k=2,3,4,5.) Of course, this is much more easily said than done, and we need to formalize what we want to test more precisely, but maybe it can be done already with the existing experimental apparatus. (I would expect a strong positive correlation which will lead to high probability for “synchronized errors.”)
Second, John, in connection with the varietal dynamics that you mentioned several times, and approximations based on low-dimensional algebraic varieties in a high dimensional Hilbert space, let me note that BosonSampling by itself is a process to reach a bosonic states which belong to a small algebraic variety of high dimensional Hilbert space. Namely, we consider the variety of decomposable degree n symmetric tensors with m variables (of dimension nm or so) inside the Hilbert space of all degree n symmetric tensors with m variables of dimension
. E.g., for n=10 and m=20 we consider the 200-dimensional algebraic variety (of decomposable symmetric tensors parametrized by 10 by 20 complex matrices) inside a 20,000,000 dimensional Hilbert space (symmetric tensors). (But for 3 bosons the dimension of the variety is only roughly half that of that of the Hilbert space.) The ability of our experimental process to “hit” closely this low-dimensional variety is already a reason for concern. The mere fact that we have a small-dimensional variety does not imply that polynomial-time approximations are possible. But it is possible that, in every such situation, small-degree polynomials in the the Tangent space to the variety allows already good approximation for realistic noisy quantum systems which are approximately supported in such a variety (or approach it).
Gil, that is an illuminating observation!
Indeed, the generic experience of simulationists is that the low-dimensional varietal submanifolds immerse in Hilbert-space as a space-filling “foam” that supports the flow of noisy/Lindblad trajectories — and thus their PTIME simulation as Carmichael unravelings — while rigorously respecting the various conservation laws, thermodynamic laws, and gauge invariances that are the “crown jewels” of 21st century quantum dynamics.
Quantum research threads that concretely are “flowing” in this dynamical/geometric direction include (for example) Hamiltonian lattice gauge theories; see for example Buyens, Haegeman, van Acoleyen, Verschelde, and Verstraete, “Matrix Product States for Gauge Field Theories” (arXiv:1312.6654) and Bañuls, Cichy, Cirac, Jansen, Saito, “Matrix Product States for Lattice Field Theories” (arXiv:1310.4118).
Can these algebraic/geometric/varietal simulation methods help to accelerate the experimental observation of nonabelian anyonic field-dynamics? Can these methods similarly be adapted to help optimize BosonSampling mises en pratique? Can these methods contribute to the rising tide of everyday technologies that press against quantum limits? Can the researchers of any young person, who is equipped with a laptop computer, an internet connection, and an inquiring mind, be lifted by this marée montante?
The evident answers to these questions are (as it seems to me and many, and by the evidence of the recent literature) yes, yes, yes, and yes.
Gil, in light of http://www.kurzweilai.net/a-record-quantum-entanglement-103-dimensions (see Zeilinger’s group’s paper that the article references), do you think that the errors would scale up with the entanglement of multiple modes of individual photons the same way you do with respect to individual qubits?
Dear Michael, thanks for the link. Indeed this is an impressive achievement. Also thanks for the excellent question. We can separate the question into two: The first: how will errors scale up for a single boson depending on the number of modes? The second: fixing the amount of errors for a single boson how will errors scale up with the number of bosons. I don’t have much to say on the first question except on noting that the answer may depend on the bosonic state (at least in our pre-quantum computer era). Gaussian states are of special interest, of course. I have a few things to say (and I have already even said a few conflicting things) on the second question and with Guy Kindler we are struggling to relate it to BKS-noise-sensitivity. For the second question I expect that errors scale up linearly with the number of bosons (or more precisely, that the threshold for doing something useful in terms of one-boson-error scales like 1 over the number of bosons).
The simulation heuristic that I discussed with Nick and Peter can tell us something in this case as well. For example, we can ask how errors scale up for a noisy quantum computer without fault-tolerance with noise tuned so that we can create a single Gaussian boson state with m modes with a fixed amout of noise, when we move to n-bosons states. This gives some challenge (less direct compared to anyonic qubits) for proponents of BosonSampling but, in this case, there are direct and explicit ways to go about it. (As I said, the simulation heuristic does not replace the need for detailed modelling.)
Thank you for that link, Michael.
From the viewpoint of varietal dynamics, the Zeilinger’s group’s work raises the geometrically/algebraically natural question: “What is the lowest-rank varietal manifold, immersed in Hilbert space, upon which pulled-back dynamical trajectories can Lindbladian/Carmichael unravel to yield the observed density matrix?”
As nearly as I can tell, this is not a question that the Zeilinger et al paper attempts to answer, for the very good reason, that (at present) no-one knows how to answer such questions (rigorously *or* empirically) .
And yet, a large (and rapidly increasing) body of practical quantum simulation experience — also compressed sampling experience, tensor network experience, quantum measurement triangle (QMT) experience, etc. — suggests that the required varietal rank ubiquitously is very much less than linear-projection arguments would suggest.
Why is this? No one knows.
Summary Computational simulations increasingly suggest that exponentially more dimensions are required of Hilbert dynamical spaces than of varietal dynamical spaces.
Corollary Varietal dynamical systems comprise (reasonably realistic, reasonably concrete) formal models for the Kalai postulates.
To make this algebraic/geometric point another way, if we ask ourselves “What might a Sure/Shor separator (in the sense of arXiv:quant-ph/0507242) look like concretely?“, one answer might be “A varietal dynamical simulation framework, requiring PTIME computational resources, that accurately reproduced the the entangled-photon dataset of Kren et al., and moreover accurately simulated too the (far more difficult to achieve) nine-decimal-place accuracy of next-generation quantum metrology triangles (QMTs).
Philosophers might debate whether a varietal dynamic simulation (with its restricted state-space) was a Sure/Shor separator sensu stricto, and yet such a dynamical framework would be — in the literal sense of a centuries-old engineering joke — “close enough for all practical purposes.” 🙂
These pragmatic varietal considerations are why we engineers are very accepting of the Kalai Postulates.
To make this algebraic/geometric point another way, if we ask ourselves “What might a Sure/Shor separator (in the sense of arXiv:quant-ph/0507242) look like concretely?“, one answer might be “A varietal dynamical simulation framework, requiring PTIME computational resources, that accurately reproduced the entangled-photon dataset of Kren et al. (arXiv:1306.0096), and moreover accurately simulated too the (far more difficult to achieve) nine-decimal-place accuracy of next-generation quantum metrology triangles (QMTs, arXiv:1204.6500).”
Philosophers might debate whether a varietal dynamic simulation (with its restricted state-space) was a Sure/Shor separator sensu stricto, and yet such a dynamical framework would be — in the literal sense of a centuries-old engineering joke — “close enough for all practical purposes.” 🙂
These pragmatic considerations are why we engineers are very accepting of the Kalai Postulates.
Hey Gil, this looks interesting: http://arxiv.org/abs/1404.3214
It is written: “Let me quote what Steve wrote about the videos: The surprising part is the superior production value relative to your typical videotaped lecture (at least for the first overview video). ”
However what Steve Flammia actually wrote about the videos was:
“The surprising part is the superior production value relative to your typical videotaped lecture (at least for the first overview video).
I think the high gloss on these videos has the potential to sway low-information bystanders into thinking that there really is a debate about whether quantum computing is possible in principle. So let me be clear.
There is no debate! The expert consensus on the evidence is that large-scale quantum computation is possible in principle.”
Readers of Gil Kalai’s Combinatorics and More may perhaps enjoy Jaeyoon Cho’s introduction remarks in his preprint “Entanglement area law in thermodynamically gapped spin systems” (arXiv:1404.7616, this week):
From the perspective that Cho’s preprint offers, Gil Kalai’s postulates can be viewed as (the beginnings of) an “area law” for correlated noise dynamics; similarly varietal dynamics concerns itself with the geometric and algebraic structures that are supported on Cho’s “measure-zero set” of Hilbert states.
Conclusion Gil’s lecture-title “Why Quantum Computers Cannot Work: The Movie!” is enjoyably provocative, and yet (as it seems to me) it is Jaeyoon Cho’s perspective that focuses our attention upon those aspects of Gil’s postulates that are the most mathematically and scientifically interesting (in the short run) and the most economically and strategically important (in the long run).
Alexander Vlasov raised an excellent point about noise, fault-tolerance, and the extended Church-Turing thesis (ECT). (In this comment, this one and the follow up just below it.) Let me rephrase what Alexander is saying:
We have a system consisting of a quantum computer + noise. This combined system is not less powerfull than the quantum computer alone. So if the quantum computer disprove ECT some *additional* effect may not restore ECT!
Alexander mentioned the analogy with horsepowers: If your car’s engine has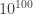
horsepowers but by some imperfection you only uses 100 horsepowers, it still has 
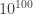horsepowers!
He offered the following analogy/thought-experiment: “Someone has working quantum computer, but after factoring test the results are encoding using standard method with addition of random numbers. So nobody may use results (without knowledge of the random numbers), but we may not say that addition of the noise reduces power of the quantum computer itself.”
This is a good food for thought!
I am not an expert in the topic so apologies if my question is naive. After watching the videos there is a point that bothers me regarding your response. You use the fact that the system is fixed to argue against various points raised (which gels like super determinism but that is a side issue), what bothers me is that you assume that the system being fixed allows an explaination for fantastic things to happen. Fixing the system and not being a general purpose computer may help explain why those fantastic events do not interfere with our understanding of physics, however it does not explain how they can happen computationally. Let me give an example: a classical system is deterministic, so it is not against the law of physics if an adversary flips a particular bit of memory during the computation to change the result. The shagreen being fixed the theoretical complexity to know which bit to flip is trivial. However, in practice if an adversary wants to find the bit to flip it can be very nontrivial. Of course you can say that this is an intuition coming from the trivial flaw and looking at the uniformity of these fantastic events with respect to the systems is misleading me to think this way. However to me this seems to border begging the question, i.e. you assume that everything we know from uniform setting and general propose compassion is misleading so there cannot be a general purpose computer. All of our intuitions about computation in practice comes from uniform setting and you seem to say none of them is valid.
Hi Reader, this is a very good question but let me try to rephrase it just to see that I understand you.
Your points are:
1) The claim that a special purpose device (or what you refer to as “the system being fixed”) allows certain “fantastic” forms of noise to be consistent with the laws of physics does not mean that such fantastic events actually happen!
2) I assume that everything we know for general-purpose computers is misleading. But the fact of the matter is that all of our intuitions about computation in practice come from uniform (= “general purpose” or “universal”) setting and I seem to say that none of them are valid.
Is it a fair description?
(I was away on a vacation and I still “owe” (perhaps mainly to myself) a few answers. So I will get to them a bit later.)
Yes, you said it much better than I did.
Let me quickly relate to the points raised by “Reader.” To the second point: it is indeed misleading to assume that everything we know about classical general-purpose computation extends to quantum general-purpose computation.
There are several things to be said regarding the first point. The modeling of noise I propose is not “fantastic.” It seems fantastic if either you take general-purpose quantum computers for granted, or if you take for granted hypothetical quantum evolutions that cannot be realized at all. It is certainly correct that some of my proposals are in conflict with people’s intuitions. For example, I propose that the rate of noise (or the chance of failure) scales up with the complexity of the quantum evolution. This is a fairly mundane and unsurprising proposal unless you take universal quantum computers for granted.
There is one thing I have never understood in your arguments. A classical computer has a bunch of internal switches (transistors, diodes, etc) and a bunch of external controls (switches, LEDs, etc). A quantum computer has a bunch of internal switches (e.g. always-on two-qubit interactions) and a bunch of external switches (e.g. classically-controllable laser pulses, photodetectors). Why do you describe quantum computers as special-purpose and classical computers as general-purpose? What would a special-purpose classical computer look like? A player piano? A computer with mostly ROM and very little RAM, like a CD player? The term “special purpose” seems important to your intuition, but I still do not understand it well enough to be able to re-explain it in my own terms.
Re what Aram wrote:
Aren’t all real classical computer special purpose (e.g. because of finiteness and physical limitations on memory, etc.)? There is no universal computer in reality, it is just a theoretical model, or are there? E.g. do you consider a MacBook a universal computer or a special purpose computer? Are we looking for a universal quantum computer or something like a quantum device that a universal quantum computer is a good model of its behaviour, the same way Turing machines are good models of MacBook computers?
Re 1: My trouble is that “fantastic” things do look really fantastic, and even if we talk about a fixed non-universal machine. OK, the machine is fixed, so _theoretically_ those things can be computed easily. The same way the halting problem for any fixed Turing machine is trivially computable. But this doesn’t mean actually taking place. I can give you a fixed machine and both of us can agree that the halting problem for this machine is decidable. However we may not be able to know whether it halts or not. That is the same issue I have with the fantastic things. They are in principle easy computationally, but I think in reality they have to computed somehow. Let’s say that the noise for your model is exponentially hard to compute classically if we give the description of the special purpose quantum machine as input. If we fix the machine then the noise can be much easier. However this easiness looks similar to ease of deciding the halting of a fixed Turing machine. In practice there are Turing machines that we can never decide if they halt or not. Same with the noise model. Yes, the description of the machine fixes the noise and makes it easy theoretically, as the description of a Turing machine fixes the answer to the question if it is halting. Why the noise for every special purpose machine can be computed easily in practice?
Re 2: My trouble is that I don’t see strong support for the claim that our intuition from classical computers do not apply to quantum computers. In other words, why do you think so? It is not just our intuition about theoretical general-purpose classical machines, it is also our intuition based on practical experience with special-purpose classical machines.
Thanks again and apologies if my questions have trivial answers or don’t make sense because of some basic misunderstanding or confusion.
Aram, perhaps the following terminology will be less confusing: a “quantum device” is a device capable of creating a certain quantum evolution (or a family of quantum evolutions); a quantum computer is a quantum device capable of achieving universal quantum computing.
(We can also relax a bit and refer to a quantum computer as a quantum device capable of achieving computationally-superior quantum computing even if not universal.)
I referred to a quantum device as “a special-purpose quantum device” and to quantum computers in the strict sense as “universal” or “general-purpose” quantum devices, but somehow this terminology confuses you.
I guess the terminology confuses me because the distinction does not seem fundamental, and does not seem to be located in the machine. If a laser has a knob which lets me control its power, then the machine is a “general-purpose” device, but if someone superglues the knob into a fixed position, then it is a “special-purpose” device? Trying to think about border cases rapidly leads me into more and more confusion over these categories.
Aram, I still don’t understand what confuses you. Maybe try to share some more “border cases”.
Aram, so let me try to break up the argument you refer to into small pieces and let me know where you do not agree or do not understand.
1) Quantum computers are hypothetical objects.
2) Quantum devices are not hypothetical: there are plenty of both natural and human-made quantum devices.
3) The behavior of noise for quantum devices may tell us, in principle, if quantum computers are at all possible.
4) For a quantum device it is possible that the noise will depend on the evolution carried by the device.
5) It is possible, in principle, that such a putative dependence over all quantum devices will be systematic.
6) For example, it is possible, in principle, that for all quantum devices the rate of noise will scale up for complicated evolutions. (For some definition of “complicated.”)
7) It is possible, in principle, that such a dependence will imply that quantum computers are impossible.
1. agree, especially if you add adjectives like “large-scale” and “stronger than classical”. I would say that small quantum computers exist.
2-3. agree
4. These terms, like “noise” and “evolution carried”, are imprecise, and without defining them more precisely it’s hard for me to answer. In particular, “noise” refers to unwanted evolution, but this is of course something not objectively defined. I think it will be hard to state this in an observer-independent way.
5-6. Again ill-defined, and here I am deeply skeptical anything will work. Note that these could be true for vacuous reasons, like defining “complicated” to mean “noisy.”
7. sure. 🙂
Dear Aram,
1) (Also relevant to your earlier comment, and reader’s last comment.) We can define a quantum computer as a quantum device capable of performing long computation on m qubits ( m fixed) with a universal collection of gates, and with negligible errors. With this definition (even for the minimal m=2) quantum computers are hypothetical, and it is widely believed that implementing quantum fault-tolerance (which is also hypothetical) is necessary for building them.
2) Your claims that noise is “subjective,” or “ill-defined,” or “not-fundamental,” are interesting, and, overall, I disagree with you. But it is mainly irrelevant here. The threshold theorem for quantum fault-tolerance is based on a certain modeling for noise, and I propose an alternative way for modeling noise.
3) Discussing quantum devices rather than quantum computers allows more flexibility in the way the noise may depend on the “intended” (or “approximated”) evolution. Both in the ordinary modeling of quantum noise and in my modeling we consider a noisy approximation (or perturbation) to a unitary (“intended” or “ideal”) evolution.
4) Of course, when we consider a specific suggestion on how the errors (or noise) depend on the “ideal evolution” we need to make sure that the dependence will be invariant for small changes of the “ideal” evolution itself. If you look at the specific conjectures presecribing my “detrimental noise” you can see that this is indeed the case.
This applies, for example, for the very specific conjecture asserting that when two qubits have large entanglement then the leak of information for them has substantial positive correlation, also for the conjecture that the rate of noise in a time-interval is lower-bounded by a measure of non-commutativity of the “ideal” evolution in that time-interval, and also for the smoothed-Lindblad-evolution description.
I think Aram’s question is: how does Nature know the “intended” evolution for a quantum device? Your framework seems to treat “intended evolution” differently than “noise”. In standard quantum mechanics, you don’t need to know the purpose that the device’s builders meant it to be used for in order to figure out how it evolves. Will the evolution your framework gives with a device has intended evolution U, and a small amount of noise be different from a device with intended evolution U’ and a small amount of noise? If U is nearly U’, the difference between them could be viewed as noise. How can Nature know which of these is the “intended evolution”?
Dear Peter,
You asked: “how does Nature know the “intended” evolution for a quantum device?”
There are two relevant levels for this question. The first refers to the conceptual framework and the second refers to the mathematical modeling. Let us restrict ourselves for simplicity to devices that implement a quantum circuit and start with the conceptual framework.
We can consider
(*) a quantum computer that has the flexibility to perform approximately any sequence of gates on a set of (say five) qubits.
(**) A quantum device that can perform approximately a certain specific sequence of gates on a set of (say five) qubits.
Probably to implement (**) can be easier than to implement (*). (Of course, this is not always the case, implementing (**) by first creating a quantum computer (*) and then using super-glue to cripple it as Aram suggested above will not make it easier.).
For (**) the nature of approximation your device achieve may depend on the device. And the device may be very specific to the evolution (or a limited set of evolutions) it is capable of performing. So for devices of type (**) the way the approximation depends on the evolution can be more general than for devices of type (*). And the specific relations for type (**) devices between the approximation and the evolution potentially deems type (*) devices to be impossible.
Talking about “the purpose that the device’s builders meant it to be used” is just confusing. You have to talk instead about “what the device is doing”.
The second level is the level of mathematical modeling. Talking about a noisy evolution as a certain perturbation of a unitary evolution is not new. The type of modeling I propose requires some limitations on what we refer to as “noise,” as well as some consistency tests that we need to pass. Most importantly, as I explained in a previous comment, the conditions on the noise should be invariant to small changes in the “intended” unitary evolution.
“Will the evolution your framework gives with a device has intended evolution U, and a small amount of noise be different from a device with intended evolution U’ and a small amount of noise? If U is nearly U’, the difference between them could be viewed as noise. How can Nature know which of these is the “intended evolution”?”
In my setting we consider unitary evolutions where the added noise is described by a POVM-measurement. (Moving from a unitary to another unitary is not viewed as “a noise,” but the noise can represent moving from a unitary evolution to a mixture of near-by unitary evolutions.) Nature does not need to know what is the “intended evolution” since the conditions on the noise are invariants to small changes of the intended evolutions and can sometimes be described without even referring to the intended evolution.
(The mathematical price we need to pay is that the noise is described by implicit mathematical conditions.)
P.S. I notice that one can still make the conceptual objection even more abstract by claiming that in nature we just have a huge unitary evolution with no devices and no objective meaning to “noise”. As I mentioned to Aram I don’t think this point of view is very useful/relevant in the specific context of the “threshold theorem/quantum fault-tolerance”. But we can nevertheless think about this very abstract point of view. Then we are simply interested in restrictions of the huge evolution to a few degrees of freedom (i.e. to a small-dimensional Hilbert spaces). For this abstraction, my conjectures propose a description of cases where we have “close to unitary” evolutions on a small-dimensional Hilbert space and they asserts that if we describe this “close to unitary” evolution as a POVM-perturbation of a unitary evolution, then this perturbation satisfies various conditions. (And it does not matter, which unitary evolution you choose for the description.)
Dear Gil,
You say
Do you actually have a proof of this statement (“it does not matter, which unitary evolution you choose for this description”), or do you just hope that your conjectures satisfy this invariance criterion?
Peter, yes. The way the conjectures are formulated make sure (or try hard to make sure) that a) they apply for a noisy evolution which well-approximate a unitary evolution, and b) they are stable under changing the “target” (or “intended”) unitary operation.
Here is the first version of my paper with Guy Kindler on BosonSampling and Noise sensitivity (also posted on my homepage and we will arxive it soon).
1) For a fixed amount of noise BosonSampling is in P. Moreover, noisy BosonSampling can be approximated by bounded-depth polynomial time computation.
2) To have robust experimental outcomes in the presence of noise one need to specify the noise with exponentially size input. So all we have is an exponential-time algorithm with an exponential size input. So this demystified the claim of “quantum supremacy.”
3) When the noise level is
or higher noise sensitivity makes it unlikely to expect robust outcomes at all.
What I am happy about the paper is that the Hermite-Fourier approach allows very concrete computation. I expect that our results kicks-in for small number of qubits (7-8) but this is something that is mainly left to experiments.
Dear Gil, I see the paper appears in arXiv? My congratulations!
My reasoning below is certainly not concerning BosionSampling and similar ideas there statistics is part of algorithm.
I also would like to point on Troyansky and Tishby [1996] work about problem with sensitivity (see reference 61 and short discussion in Scott’s work you are citing as [2]). I myself hear the presentation in 1996 and have a vague impression that it is very close to ideas of your work.
Dear Alexander, many thanks for your comment! I will certainly look carefully at the paper by Troyanski and Tishby. (Naftali Tishby is a colleague here at HUJI and a close friend since the mid 70s. We chatted briefly about BosonSampling and other physics “gadgets” potentially relevant to quantum computing some months ago.)
Dear Gil, I am glad that you know an author – I myself know about the interesting issue only due to rare proceedings of the conference. Frankly speaking, then I read first article about BosonSamping my initial impression was: “but how they avoid the problem mentioned by Troyanski and Tishby?” and I am still not completely understanding that even now.
Alexander Vlasov raised an excellent point about noise, fault-tolerance, and the extended Church-Turing thesis (ECT). (In this comment, this one and the follow up just below it.) Let me rephrase what Alexander is saying:
We have a system consisting of a quantum computer + noise. This combined system is not less powerful than the quantum computer alone. So if the quantum computer disprove ECT some *additional* effect may not restore ECT!
Alexander mentioned the analogy with horse-power: If your car’s engine has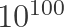
horsepower but by some imperfection you only uses 100 horse-power, it still has 
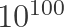horsepower!
One idea which seems implicit in Alexander’s thinking is that nature has superior quantum computational powers (quantum supremacy, for short) even if noise does not allow us to make use of these powers. I think that this point of view is not correct for the following reasons. (The BosonSampling previous comment and paper exemplify these points quite well.)
1) Quantum computers are hypothetical and general quantum evolutions that quantum computers can perform are also hypothetical.
The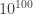
-horsepower car is only in our imagination.
2) Noise sensitivity means that realistic noisy quantum systems depend on exponential input size.
When you or nature implement a state which seemingly requires exponential time computation(in some parameter
, robust outcomes depends on exponentially many parameters in 
describing the noise.
3) It is unuseful and incorrect to think about mixed-state (say bosonic or anyonic states) evolutions as “really” representing some pure state evolution “known” to nature but unknown to us. (This is also related to Nick Read parenthetical comment displayed above. ) A main reason is that the expression of pure states and mixtures is not unique.
(Analogy: it is unuseful and probably incorrect to think that at any given moment there are two elephants in your office which, having opposite signs, cancel each other.)
In the car with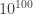
horse-powers example, this means that if your imperfect car has 100 horsepower it is physically impossible to distinguish between a description of an imperfect 
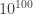horse-powered car and an imperfect 100 horsepower car and we should prefer the second explanation.
Of course the crucial hypothesis is
4) Realistic noisy quantum systems can be simulated in BPP.
Correct asymptotic modeling of realistic noisy quantum evolutions man-made or natural gives us an evolution that can be simulated efficiently on classical computers.
No, I did not make any claim about real computational power of Nature. I simply meant that idea about possibility restoration of ECT due to noise (found in your exchange elsewhere) seems wrong due to thought experiment I mentioned.
Dear Gil, I doubt, it could be accepted without additional explanations – I suppose, if we could see some car with 10^100 horse-power engine, we could very simply distinguish that from car with 100 horsepower after simple research – in some way we may distinguish ship with power plant and sailing ship even if they have the same speed and size, because we may see that the power plant is working and how the ship is using only tiny fraction of the power.
In the same way, if we are supposing usual model of quantum computer, we know that the model (“power plant”) may factor integers in principle and the model with noise is an analogue of slowly moving ship with power plant.
In such example your argumentation looks like idea, that the power plant is only illusion and, in fact, both ships are moving due to wind.
But such a case looks like you could suggest instead of usual model of quantum computation some model that may be simulated classically even without noise – then you indeed would say that due to noise we may not distinguish such models and to claim quantum supremacy.
Dear Peter,
You wrote: “So if ‘quantum computers cannot work’ is the premise of your theory, does your theory lead to any concrete predictions besides “quantum computers cannot work”? If it doesn’t, then I can’t help thinking that there really isn’t much substance to it.”
Ahh ok, as promised (mainly to myself) let me collect some predictions, insights and connections that I propose.
Two Meta Points
First, I agree that we should seek and explore concrete, wide and bold predictions related to the failure of quantum computers but there is an issue to be taken also with the claim that there isn’t much substance to the premise “quantum computers cannot work” taken on its own. (Of course, we are talking here about computationally superior or even universal quantum computers.) The many proposed avenues towards “quantum supremacy” give you a large front of predictions merely from the premise that “quantum computers cannot work” in a similar way to the many predictions and insights driven from “3-SAT is intractable”.
My expectation is that for many physical models and many proposals for quantum simulations, quantum fault tolerance and quantum computing, adding the premise “no quantum supremacy” or “no quantum fault-tolerance” will teach us a lot about the physics. (The extremely simple BosonSampling is a good example for that.)
The second point actually supports your claim that we need to go beyond “quantum computers are impossible.” Since universal quantum computers are hypothetical, some insights for why they might fail are counter-factual and to become interesting they should be extended to quantum systems without superior computing capabilities. As Greg Kuperberg puts it (in a different but related context):
Quantum devices that demonstrate superior quantum computing are like cars that plunge over a cliff. We need to understand and model how cars behave in ordinary circumstances before they plunge over the cliff.
For example, very natural explanations for failure of universal quantum computers are:
1) For any attempt to build a universal quantum computer the noise rate cannot be lowered below the threshold required by the threshold theorem.
2) For any attempt to build a universal quantum computer there will be some noise of arbitrary nature on the entire Hilbert space.
Both these explanations were suggested by people soon after the threshold theorem was discovered, and both may very well be correct and relevant, but to make them useful you need to extend them and explain the law for general noisy quantum systems which will imply that any attempt at a universal (or superior) quantum computer will demonstrate 1) and/or 2) . In other words, you need to understand the behavior of the car before it plunges over the cliff.
Predictions
Ok, now for predictions:
A) my basic hypothesis
1) Quantum speed-up requires quantum fault-tolerance
2) Quantum fault-tolerance is not possible.
3) The failure of quantum fault-tolerance and quantum speed-up can serve as a powerful conceptual and computational tool in physics.
A large part of my work can be described as trying to put these statements on formal grounds. The physics prediction that quantum fault-tolerance is not possible is detailed in the next points. (There are also fairly concrete related mathematical conjectures.)
The informal conjecture/prediction that quantum fault-tolerance is necessary for universal quantum computing is quite common. I expect that this is the case for any fixed number of qubits with a universal class of gates. There are several proposals to demonstrate some forms of quantum speed-up while avoiding quantum fault-tolerance and the clear prediction is that all these proposals will fail experimentally.
There is a refinement of A) which refers also to classical computation.
1′) Any form of computation (beyond “noisy bounded depth computation”) requires fault-tolerance.
2′) Every physically feasible mechanism for fault-tolerance is based on a repetition mechanism, which allows only classical computation.
B) Other important ingredient of my point of view are:
For general quantum systems, there are systematic relations between the noise and the quantum evolution. For realistic implementations of quantum circuits there are systematic relations between the target state and the noise.
For the ordinary models of noise for quantum computers, the noise depends on the evolution (in a certain limited way), and fault-tolerance allows the noise to be essentially independent from the target state.
2) Implicit conditions for modeling the noise rather than an explicit model.
For all the noise models below, both those describing the behavior of few qubits and those describing very general physical systems, the noise is described in terms of implicit (or “circular” if you wish) conditions and not explicitly as in common modeling in the context of fault tolerance (both in the CS threshold literature and the Hamiltonian noise models for threshold theorems).
Of course implicit conditions/definitions are common in mathematical modeling in physics.
C) The nature of errors for realistic implementation of noisy quantum circuits
The whole idea of my conjectures in this direction was to find ways to distinguish systems with fault-tolerance, ways that can be tested on a small number of qubits.
Here we consider a realization of quantum circuits: so we assume the qubit/gate model and we assume to start with that gate-errors are of general form and that errors on gated qubits (or qudits if you wish) are positively correlated.
1. Correlations:
1.1 Two-qubits behavior. Any implementation of quantum circuits is subject to noise for which errors for a pair of entangled qubits will have substantial positive correlation.
1.2 Error-synchronization. For complicated target states highly synchronized errors will occur.
1.3 Error-rate. For complicated evolutions (or for evolutions approximating complicated states) the error rate (in terms of qubits-errors) scales up with the number of qubits.
Error-synchronization can be mathematically derived from a (strong) form of the 2-qubit behavior. Error-synchronization implies the error-rate conclusion if we assume that the error rate is constant in terms of trace-distance: For correlated errors the natural measure of rate in terms of trace-distance becomes sharply different than the rate in terms of qubit-errors (which is relevant for quantum fault-tolerance). This gives a clear prediction that error-rate in terms of qubit errors for highly entangled states (we will see examples below) will scale up linearly with the number of qubits.
Of course, correlated errors as an obstacle to FTQC were considered very early. (John Preskill, Robert Alicki, John Baez, Leonid Levin (briefly), and others.) The idea that error-rate scales up can be found in various places. (E.g. I think that this is Preskill’s interpretation to some of Alicki’s conjectures.) The relation between correlation and scale up of noise-rate appears to be new.
The prediction here in brief is that every attempt to build a quantum circuit of general type will face noise with the property that the error-rate, in terms of qubit-errors, scales up linearly in the number of qubits, and the errors exhibit strong positive correlation. This prediction (also with its more precise mathematical forms) can be tested on plenty of experimental attempts towards quantum circuits as well as for other controlled and natural quantum systems.
2. Encoded qubits
Encoded qubits cannot be stable. (They cannot be substantially more stable than the raw qubits used for constructing them.)
(There is some similarity between this prediction and Dyakonov’s “Axiom 1,” from his recent skeptical paper.)
The constants. The constants in the above conjectures are important. I suppose that the realistic constants are such that they will come to play for small systems with few qubits. The mathematical formulation. The mathematical formulation of the above conjectures is also important and it can be found in my papers (with some modifications based on my discussion with Aram Harrow.)
D) predictions for attempts to create stable surface codes via superconducting qubits
There are several groups attempting to create stable encoded qubits based on surface codes applied to superconducting qubits. These attempts will bring my conjectures to test. For example, Martinis proposed to create, in the near future, stable qubits via surface codes based on roughly 20 “raw” qubits and, in a few years, encoded qubits based on distance-five surface codes, where each encoded qubit depends on about a hundred raw qubits. (There are even less immediate plans for extremely stable encoded qubits based on roughly 1000 “raw” qubits.) In a nutshell, my conjectures predict that very positively-correlated errors for individual raw qubits will emerge, leading also to error rate scaling up linearly with the number of qubits. In particular, the prediction is that all these attempts of creating much stabler logical qubits based on surface code will fail. My predictions should be strongly manifested even for the encoding based on 20 raw “qubits” and, in fact, even for a careful analysis of noise, for the already successful demonstration of encoded qubits based on 4 or 5 raw qubits. (E.g in this paper http://arxiv.org/abs/1402.4848 .)
E) The nature of errors for general noisy systems
Another part of my work is to try to express laws of “no quantum fault-tolerance” for the most general quantum systems.
1. Lower bound on the rate of noise in terms of a non-commuting parameter.
For a noisy quantum system a lower bound for the rate of noise in a time-interval is a measure of non-commutativity for the projections in the algebra of unitary operators in that interval.
The precise non-commutativity measure is still negotiable. When we consider implementations of noisy quantum circuits this is quite compatible with the standard assumption of constant rate per computer-cycle.
This lower bound came from discussions with Ronnie Kosloff and Michael Khasin. A somewhat similar picture, with some twist, is arising (completely independently) from symplectic geometry and quantization. There, the setting is as follows: We make a distinction between general POVM’s and von-Neumann observables which are special cases of POVM’s (called also projector valued POVM’s). The “unsharpness principle” asserts that noisy quantum evolutions must be “far” from those projector valued POVM’s. The amount of unsharpness is bounded below by some non-commutativity measure. In the symplectic setting it can be proved that non-commutativity provides a lower bound for unsharpness. (There is some difference from our setting as here we can talk about ideal unitary evolutions and do not talk about noise for systems approximating unitary evolutions. However, in the case of quantum computers the unsharpness principle directly applies e.g. when we restrict the analysis to a subset of qubits.) For more and references see this post.
2. smoothed Lindblad evolutions
Noisy quantum evolutions are subject to noise with a substantial correlation with smooth Lindblad evolution. Or in a slightly stronger form: are subject to noise with a substantial correlation with its own smoothing.
We discussed it extensively in a previous thread.
3. The internal clock of an evolution
It makes sense to base the smoothing on an intrinsic clock which depends on the evolution and to base this internal clock, as proposed in the first item, on a non-commutativity measure for time intervals. (Although the prediction above should apply with worse constants also for the “global” clock.)
4. The two types of noise.
When we have two interacting quantum systems A and B (where often A is the system and B is the environment) we necessarily have two types of noise. (Here “noise” refers to the law for how system A deviates from a unitary evolution on its own Hilbert space.) One type represents the intrinsic structure, symmetries and clock of B and the other type represents the intrinsic structure, symmetries and clock of A. For example for a Bose-Einstein state on a bunch of atoms, one type corresponds to independent noise for the individual atoms while the other type represents fluctuations of the collective BE state itself. (The second type is the one represented by my smoothed Lindblad.)
5. A mathematicsl conjecture – Noise described by smoothed Lindblad evolutions does not allow quantum fault-tolerance
(Mathematical) prediction on quantum fault tolerance: We discussed smoothed Lindblad evolutions at some length in a previous thread. (In fact the discussion in that thread and a related remark by Bruno Nachtergaele have led to item 3.)
Since quantum fault-tolerance is based on controlled non-unitary evolutions, extending the conjecture to this case requires additional effort. One way to go about it (which could be simpler) is to consider a mathematical model by Ben-Or Gottesman and Hassidim (this work came about from some questions posed by Robert Alicki in his 2005 Jerusalem visit).
The (mathematical) prediction for Ben-Or-Gottesman-Hassidim model
Here is the simplest version of a mathematical conjecture for “quantum computing without quantum fault tolerance can be reduced to classical computation.”
We start with a circuit which has a very simple noise as described in the paper of Ben-Or-Hassidim- Gottesman: BGH had three versions: one which allows log depth computation (going back to a paper of Dorit, Michael, Russel, and Noam,) one that allows poly-time depth and one that allows exponential depth. Interestingly, when you have a combination of these types of noise the combined effect is based on a best-case form of noise!
Now we make an additional assumption on the noisy evolution:
(It may be enough to require that the smoothed noisy evolution has positive, bounded away from zero correlation with the original evolution.)
Then the conjecture is:
Under the smoothing assumption (*), for all three versions of noise you cannot go beyond (noisy) bounded depth quantum computation.
The smoothing operation is described as follows:
we consider a quantum circuit that runs for T computer cycles, we let
denote the intended unitary operator for the t-th step, and we start with a noise operation 
for the t-step. (E.g., one of the three types of noise considered by Ben-Or, Gottesman and Hassidim.)
Then we consider the noise operator
Where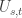
denotes the intended unitary operation between step s and step t. (t can be larger or smaller than s) K is a positive kernel defined on [-1,1].
A result by Greg Kuperberg and me implies that you really need the sum to go over “positive” and “negative” times.
I expect that it is also possible to develop a similar conjecture for the ordinary settings of the threshold theorem.
6. The noise systematically “depends” on future evolution
One clear emerging prediction is that for noisy quantum evolutions there is a systematic relation between the law for the noise at a time interval and the entire evolution (including the future evolution)!
It is not that the evolution in the future causes the behavior of the noise in the past but rather the noise in the past leads to constraints on feasible evolutions in the future (in the regime where the “car does not plunge over the cliff”.)
Such dependence can occur for classical systems. Without refueling capabilities, the risk of space missions in take-off strongly depends on the details of the full mission. (Such dependence can be eliminated with refueling capabilities). A principle [or even a temporary reality] of no quantum fault-tolerance implies that in the quantum setting such dependence cannot be eliminated.
F) Bounded depth approximations
Here the prediction is quite clear:
(Noisy) bounded depth polynomial size quantum computation is the limit for quantum states achievable by any implementation of quantum circuits (and more general realistic quantum evolution).
An even more detailed picture is the following:
a) Noisy bounded depth computation describes the computational power of every physical devices without fault-tolerance and
b) Every fault-tolerance mechanism in nature is based on a repetition mechanism. It allows only classical computation.
(Of course, once you have robust classical information you can apply, on top, other forms of classical fault-tolerance as well.)
Limits for cooling/refrigeration
One interesting aspect of this prediction (related also to several other things) is that when we consider certain classes of physical states (described, e.g., in terms of their symmetries) there is a limit to how close they can be to pure states. The reason is that when you fix this symmetry class, because of different representations of mixed states, for larger entropy the mixture can be represented by bounded depth circuits. The prediction is thus:
Within a symmetry class of quantum states (or for class defined in a different way) the bounded-depth requirement provides an absolute lower bound for cooling.
Obstruction for cooling/refrigeration in certain systems arising in quantum chemistry were observed by Ronnie Kosloff and collaborators.
Noisy bounded depth computation for certain classical systems.
The idea that noisy bounded depth computation represents the complexity class of systems without fault tolerance can be relevant to other related issues. For example one can conjecture that this is the limit of computations that can be described by 2D Navier-Stoke evolutions. It is an interesting question raised by Terry Tao what is the situation for 3D NS equation. (Tao conjectures that such systems support fault-tolerance, and hence classical computation).
The reason to refer to “noisy bounded depth computation” is that circuits with n bits input of bounded depth and polynomial size still allows to compute arbitrary functions on log n bits. So adding noise even on top of bounding the depth is required if we wish to have a notion independent from the scale. (But there may be other ways to go about it.)
Deriving a bounded-depth restriction for a class of physical systems or adding such a restriction will lead to additional interesting non-classical conserved quantities for such systems.
Anyonic systems
I also predict that the bounded-depth driven entropy lower bounds applied to anyonic systems will be higher, by a large margin, than what is needed for topological quantum computing. So this leads to the following prediction that we discussed at some length on this thread.
Stabe anyonic qubits, and stable anyonic states cannot be constructed.
(to be continued)
Predictions (cont)
G) Fluctuations in the rate of noise and forms of decay for systems with weak interactions
Another source of predictions comes from unrealistic properties of Hamiltonian models of noise which allow quantum fault-tolerance. There are several works where the noise is described in terms of Hamiltonians and is supposed to be physically realistic. (See this paper of John Preskill and references there for several earlier papers.) Those works gradually allow, on the one hand, more general correlations for the noise, and, on the other hand they are more restricted than the CS models where the noise can be adversarial. One nice mathematical feature of these works is that the ability to have quantum fault-tolerance depends on a single parameter, the norm of a certain operator which needs to be small enough. The physical prediction from “no quantum fault-tolerance” is very clear: For realistic interesting quantum systems the operator-norm relevant to quantum FT is unbounded. This prediction has bearing on important qualitative and quantitative issues regarding noisy quantum systems.
Robert Alicki also regards the small (or bounded) norm hypothesis in the Hamiltonian threshold literature as unrealistic.
1) The square-root N fluctuation
Fluctuations in the rate of noise for interacting N-elements systems (even in cases where interactions are weak and unintended) scale like N and not like √N .
The nice thing about Hamiltonian noise models is that there is a simple sufficient condition for quantum fault-tolerance, namely that a certain operator-norm is below some threshold.
One apparent consequence of this assumption on Hamiltonians noise model is that the rate of noise has a Gaussian behavior. When there are N qubits, the fluctuation in the number of errors after a unit time behaves like
and the probability of large deviation from this value is exponentially small. (Of course, this property, while sufficient, is not necessary for quantum fault-tolerance.)
My prediction is that for interacting physical systems, even when the interaction is undesirable and weak, the fluctuations in the error-rate will behave like the number of particles and not like the square-root.
2) Fluctuations for superconducting qubits
One nice place to test this (that I discussed with Aram Harrow, Nadav Katz and a few more people) is for physical implementations of very stable qubits, and in particular for superconducting qubits. Thinking about a superconducting qubit as being built from a large number of microscopic elements gives an opportunity to check the
hypothesis. (At least from a quick look at the relevant literature it looks like superconducting qubits do not obey the square-root rule.)
3) Exponential decay time
This prediction may also be related to tails for the decay time (or life time) for various physical entities. Statistical independence for a large number of components suggests an exponential decay, but, also here, there are good reasons to think that statistical independence will be violated in ways that makes a qualitative change. Also here superconducting qubits are good examples.
H) Noise sensitivity and other insights related to BosonSampling
Since I discuss it in an earlier comment and in a recent paper with Guy Kindler, (Here is a videotaped lecture about it) let me just briefly mention a few things.
A very clear prediction coming from the results of Guy and me is:
Robust experimental outcomes for systems of non-interacting bosons can be approximated by low-degree Hermite polynomials and this gives an effective tool for computations.
Two vast generalizations are:
1) In wide contexts, robust (or noise-stable) quantum physics experimental outcomes are computationally feasible and stability to noise can lead to effective computational tools.
Another way to say it is that robust experimental outcomes for quantum systems need to be stable under fluctuations of the description of the problem. Such stability may lead to effective and efficient computations.
This idea seems to be familiar in actual computations in quantum physics (and chemistry). While I am not aware of earlier attempts to connect noise-sensitivity with computational complexity, the general idea that robustness implies feasibility has several manifestations in the theory of computing (but is not universally true).
As non-interacting bosons represent a low dimensional algebraic variety inside much larger relevant Hilbert spaces. We can speculate what the analog for the Hermite-expansion might be:
2) For varietal quantum states (quantum states described by a low dimensional algebraic variety in a large Hilbert space), robust experimental outcomes for such states can be approximated by low degree polynomials on the tangent planes.
The BosonSampling proposal demystifies some beliefs regarding quantum computation. An example is the claim that quantum physics firmly predicts (superior) quantum computation. For BosonSampling there is no dispute that (without fault-tolerance) systems cannot be scaled up. The basic framework of quantum physics does not give a clear prediction if breakdown happens for 1000 bosons or for 8 bosons. Similarly, the basic framework of quantum physics does not give a clear prediction if realistically the level of noise for attempts to build quantum circuits is below the threshold or rather is unbounded, and scales up with the size of the system. It also does not tell what the involved constants are.
I) The ability of classical simulation
One prediction from the hypothesis of “no quantum computation speedup” or “no quantum fault-tolerance” is that computations in quantum physics can, in principle, be simulated on a digital computer. (Or technically speaking: they can be simulated by a probabilistic classical computer.)
There are of course several caveats coming with this prediction. First this prediction talks only about computational complexity obstacles for simulations. So if a physical system requires a simple polynomial-time computation but the input size of this program is intractable, then we still refer to it as a computation that can be simulated, in principle, by a digital computer. Second, we need to talk about simulations of robust processes – namely processes where we can get a firm experimental outcome (that can also be a firm stochastic outcome). Third, simulating a physical process requires having a model and knowing the relevant parameters. There could be obstacles (even in principle and even of computational-complexity nature) for finding the model or for finding its parameters. In classical computation, it is possible (and is the basis for cryptography) that a problem is computationally easy once certain parameters are known but without them it is intractable. And, of course, when we talk about computations in quantum physics we refer only to realistic quantum systems. There are plenty of theoretical models (in quantum physics as in other areas) that demonstrate computational intractability.
Even with all these caveats the prediction about classical simulability is powerful. There are quite a few examples of computations from quantum physics where apparently superior computational power is needed. We witness robust physical behavior of fairly complicated systems and we witness larger and larger computational power needed to allow predictions that fit experiment. We need to study these cases one by one. (As a matter of fact with Nadav Katz, Ronnie Kosloff and Dorit Aharonov we plan to look carefully at several examples.)
What about non-robust computation? After all nature “simulates itself” (or “computes its own evolution”) whether the results are robust or not. Why should we make a distinction between robust and non-robust processes? This is again a topic which the story of BosonSampling demonstrates nicely. For BosonSampling, getting close to a bosonic state described by a Gaussian matrix is very sensitive to noise, meaning that the outcome depends on exponentially many parameters (in terms of the number of bosons) which are needed to describe the noise. (Of course, for a large number of bosons it will simply not be possible, by us or by nature, to get close to a state described by a Gaussian matrix.)
Heavy atoms. One place to look for quantum systems that may require heavy computation is at computations for heavy atoms. Some physical parameters of large atoms are extremely robust and can be computed experimentally extremely accurately. While for the Hydrogen atom computations from first principles also famously give extremely accurate matching results, the situation for heavier atoms is different. Is this a case where QFT computations require superior computational power? (This was Feynman’s motivation for quantum computers.) Reasons to doubt that this is the case are: first we do not have an available model and computation based on it (even coming from QFT) for computing robust physical parameters of heavy atoms. And second there are some claimed effective methods allowing predictions of experimental outcomes for heavy atoms.
This humorous picture of the quantum landscape is from my QSTART short talk. Quantum computers are represented by a hypothetical tower of Babylon on the left. A premise or a principle of “no quantum fault-tolerance” (or no computational superior quantum computing) can be seen as a moderate earthquake, strong enough to remove this tower, that will have implications on the interface between quantum mechanics and thermodynamics, relativity, and even classical physics. It will require and enable enforcing the foundations of computations from quantum field theory (represented by a bridge).
J) Insights and predictions of general nature and relations to questions in the foundation of QM.
I predict that a principle of “no quantum fault-tolerance” will shed light on familiar issues and controversies in quantum physics and may enable to capturing some foundation uncharted territories into the scientific grounds. No-quantum-fault-tolerance (or no-quantum-superior-computation) will be related to other laws, conceptual issues, and computational methods, in quantum physics. It may also lead to justifications for routine yet unjustified or heuristic computations in quantum physics.
a) Internal structure and symmetry
Noisy quantum computers with quantum fault tolerance exhibit a picture of quantum systems which is quite different than what we witness in reality. The noise largely represents the “computational basis” and thus the very fine building blocks of the system, and does not represent the coarser structure and symmetry of the emerging states. In reality the very fine internal structures of a quantum system can be of small relevance. (We need to be thankful for this as it allowed studying coarser structures without understanding the fine structure, throughout the history of science .)
Every quantum system is subject to noise that respects its symmetry.
Here the prediction is e.g. that when you create a bosonic state the noise will be of bosonic type, and when you create a fermionic state the noise will be of fermionic type and will hardly reflect some fine internal structure. Moreover, I predict that this property can be mathematically derived from other conjectures like the one about smoothed Lindblad noise.
b) Locality as an emergent phenomenon
Locality means (on the combinatorial side) that quantum interactions are limited to very few particles (qubits) and (on the geometric side) that those involved particles are confined geometrically. Enforcing local rules on the nature of noise (approximations) allows highly non-local behavior for controlled systems via quantum fault-tolerance. I predict that the various conjectures on the nature of noise, will lead to “locality” emerging both for the law for the noise/approximation and for the law for the approximated evolution.
c) The emergence of Spacetime.
In various areas of physics, when the same physics can be demonstrated with systems of different geometries, this is important and people are quite happy about it. Once universal quantum computers are possible, any physics (more precisely any quantum evolution or quantum state) can essentially be demonstrated on an arbitrary geometry. Something similar can be said about time: with quantum fault-tolerance any physical evolution can be, in principle, time-reversed, and without “quantum fault-tolerance” this need not be the case. We can ambitiously propose the following slogan
Well, while space (of geometric nature) and time can be seen as predictions of “no quantum fault-tolerance,” both space and time were considered before 🙂 . The idea that time emerges from decoherence is certainly quite old and I saw it attributed to Seth Lloyd. The idea that the arrow of time emerges from thermodynamics is even older.
d) The information firewall black hole paradox.
The firewall black hole paradox is discussed, e.g., here and here. There are related exciting issues in the classical mathematical theory of gravitation, and moving to the quantum theory makes the discussion more hypothetical and philosophical but still very exciting. There is a recent attempt by Harlow and Hayden to solve the AMPS firewall paradox using computational complexity. This is quite problematic since the fact that something is not efficiently computable does not mean that we do not have the information needed for the computation. (Harlow and Hayden mention in their paper various explanations around this but those are not so convincing.) Since the issue is essentially about information and not about computation, we may try to assume that the computation power (for everybody, Alice Bob, Charlie…) is unlimited, and only information is limited. (Also in wider contexts, Nature should be understood in terms of information theory and not via computational complexity.)
When we take this approach we need to pay a price: we cannot talk about closed quantum systems. For those, everybody can (in principle) compute everything from the initial conditions, and if we allow this type of computation, the paradox (along with many other basic physical insights like “no signaling”) goes away. What we can do is to talk about open quantum systems, namely to assume to start with, that we consider unitary evolution on a large Hilbert space where we have access only to a smaller subspace. (So this is the setting of noisy quantum evolutions.) And the small Hilbert space will represent a good chunk of the physical situation outside and inside the black hole.
I expect that, with the standard assumptions on quantum noise, the black hole firewall paradox remains equally powerful (even with stronger informational foundations) for open quantum systems as well. (For example, we can send many Alices rather than one to overcome the noise, and we can take quantum computation for granted.)
However, conditioned on a no quantum fault-tolerance principle we have a chance to resolve the paradox . In particular, the hypothesis of positive correlations for information leaks for entangled subsystems seems relevant. If so, then in turn, we may gain insight on the quantitative aspects of this hypothesis. Note that my no-quantum-fault-tolerance conjectures are of information-theoretic nature and not of computational complexity nature.
In a series of recent papers (arXiv:1306.0533 , arXiv:1402.5674 , arXiv:1403.5695 ) Leonard Susskind (and collaborators) studied the paradox and posit that the paradox goes away by an appropriate understanding of the ER=EPR principle of Maldacena and Susskind. A crucial aspect in the argument is that Alice does not have “sufficient quantum-computational power,” but rather demonstrates “ordinary interaction with the environment.” Thus a crucial ingredient of Susskind’s endeavor is to find a mathematical distinction between “ordinary interaction with the environment” and “quantum computational power.” Such a mathematical distinction is, of course, at the heart of my work. But instead of making a distinction that will apply just to poor Alice, perhaps the simplest principle to consider is simply that “quantum computational power” beyond classical computation is universally impossible.
e) Various other things: A principle of no quantum fault-tolerance may be related to various questions in the foundations of QM and related controversies. Here is a partial list: The measurement problem; quantum analog of Onsanger principle; the time-energy uncertainty principle; QM and free will. A list of fifty or so issues related to the debate regarding quantum fault-tolerance can be found in this comment over Lipton’s blog and subsequent comments.
A 2000 quote in a 2014 perspective
Finally, here is a quote from a 2000 discussion on quantum computers that was mentioned above in this thread: “Peter Shor (March 2000): If there are non-linearities in quantum mechanics which are detectable by watching quantum computers fail, physicists will be VERY interested (I would expect a Nobel prize for conclusive evidence of this). Of course, quantum computers could also fail for other reasons. In some other posts in this thread, John Baez has pointed out a gap in our theory of quantum fault-tolerant computation having to do with how fast the multi-term pieces in an error Hamiltonian go to zero. I expect this will eventually be resolved satisfactorily eventually, but if quantum computers fail for this reason it won’t be anywhere near as momentous.”
I completely agree with your 2000 assessment, Peter, that quantum computers can fail for reasons related to modeling quantum noise. In my view a crucial gap in the theory of quantum fault-tolerance is what I refer to as “the trivial flaw.” The theory deals with the car after it plunges over the cliff. (At this moment it can either fly or not fly, and you miss the crux of the matter.) I think that now in 2014 we can safely disagree with the spirit of the last sentence. (Of course, on logical ground it is almost a tautology.) Demonstrating “quantum supremacy” will certainly be momentous, and (even more) so will be some breakdown of quantum mechanics. I find the former possibility implausible and the latter one very implausible. Given the way our understanding of quantum information has evolved since 2000, the many connections with various areas of quantum physics, and the justified scale up in interest and importance, it is fair to say that even if quantum computers fail for “mundane” reasons having to do with modeling quantum noise, understanding it will be quite momentous. I predict that this possibility will prevail.
best regards, Gil
I suppose there is a large literature on exponential decay and violation of exponential decay. Anyway, I cam across the following paper: https://phys.org/news/2017-10-violation-exponential-law-quantum.html
Hi Gil,
Let me try to explain the very surprising consequences of one of your predictions:
We already know that the standard formulation of quantum physics appears to be computationally difficult (I am talking about the formulation without smoothed Lindblad evolution).
What you are saying is that introduced noise will make the system behave differently from its current predictions and make it easier to simulate.
Right now, particle physics experiments are simulated using lattice QFT, this simulation is computationally very intensive, and simulating particle physics is believed to high computational complexity. If we extrapolate your prediction, you predict that particle physics experiments will actually behave differently from the standard predictions, and in a way that is easier to simulate.
Is this correct, or is particle physics for some reason immune to your hypothesis?
Hi Peter,
Certainly particle physics is not immune to my hypothesis.
As I mentioned, we do try to look at examples where very intensive computations are needed to exhibit very accurate experimental outcomes. It is not so easy to point a specific such example.
Of course, the belief that simulating particle physics requires –in principle– high computational complexity is in conflict with my point of view. What I would expect is that there are (again, in principle) effective ways to simulate (robust and realistic) particle physics experiments: either there are effective efficient ways toward the standard predictions, or that the standard predictions loose their relevance for complicated systems where, on the one hand, they become computationally intractable and, on the other hand, the effect of noise in the actual experiments becomes stronger.
Anyway, it will be quite helpful if you can suggest a concrete particle physics simulation based on lattice QFT (or another thing) which requires heavy computation and where you would suspect that the accuracy of the predictions it gives cannot be matched (in principle, or just in practice) by effective efficient computations.
Just to be sure that we are on the same page, I am talking about predictions regarding robust realistic experiments. Of course, I refer here to computations “from first principles”. When your computation involves e.g., finding unknown parameters based on optimization of some sort, then scientific computations (in physics and other areas) can become intractable. This is relevant since the (often, unknown) finer structure in particle-physics systems is estimated using essentially effective computational methods. The effect of the fine inner structure can also be regarded as “noise.” Also look at the other caveats regarding this prediction.
One speculation is that conditioning on robustness-to-noise of quantum systems (or on a principle of no-quantum-fault-tolerance of some sort) may lead to effective computational methods. The BosonSampling case where you can have (above a certain low noise level) good approximations using low-degree polynomials is a very simple such example. (Actually, this may already be implicit in some physics calculations.)
Finally extrapolating on your point: do you expect that particle physics systems manifest some quantum fault-tolerance capabilities? Or perhaps they manifest quantum computing without quantum fault-tolerance?
Maybe Peter has a different answer, but there are a large number of full-time researchers working on lattice QCD who would be delighted to be able to replace their quantum simulations with classical ones.
http://arxiv.org/abs/1203.1204
In general simulations here are very computationally intensive and are not as precise as experiments in calculation properties of the neutron and proton.
I would suggest distinguishing complexity of physical process and complexity of mathematical models used in computational physics. Very often structure effective computational method may not have any relation with initial process. For example, just paper mentioned by Aram uses statistical model in imaginary time for modeling of some property of quantum system. IMHO, Feynman use term “simulation” just to avoid such situation. So, formally, many effective computational models used in modern QFT are not direct simulations of particle physics and so Gil’s ideas not necessary should be relevant for them.
According to Wikipedia, the reason we don’t know the fine structure constant better is not that the experiments aren’t good enough, it’s that we can’t calculate the magnetic dipole moment of the electron precisely enough.
The Wikipedia article mentioned by Peter uses results of 2007, yet another Wikipedia article http://en.wikipedia.org/wiki/Fine-structure_constant uses more recent theoretical calculations of 2012 and claims that errors for theory and experiment are about the same. But it is again strongly related with used mathematical methods. Some asymptotical series may be successfully used for precise calculations in QED due to small value of some constant, but it does not work in more general case if corresponding constant is bigger, e.g. in QCD.
Thanks Peter, Aram and Alexander for the comments and links, and Alexandre for the links to your paper. As I said in the comment there is a slow-going project here at HUJI to look for examples of quantum systems with strong case for “quantum supremacy” from atomic or nuclear physics or even particle physics. Certainly some QED computations are very natural candidates. (Aram, Since you brought up QCD, can you mention a couple of specific QCD computations suitable for that purpose?)
From Peter’s remark (and link) I learn that theoretic computation from first principles for the magnetic dipole moment of the electron are extremely precise but are not as precise as we wish them to be. Famously and amazingly we can get accuracy of 10-15 digits. At the end it was not clear to me if in this case the experimental methods are more accurate or not and also (more relevant to our project) if they are in direct competition or rather complementing methods for computing the fine structure constant.
Anyway, if I understood Peter’s point it was that without quantum computers theoretical QED computation are behind in precision compared to the experimental results (and there are various such examples) and that with quantum computers we will be able to efficiently make the precise theoretical computation.
My question is, Peter: with quantum computers can we make efficient computations for the magnetic dipole moment of the electron with precision of hundreds and thousands digits (like the computation of π and e in mathematics)? If so it looks that quantum computers will allow us to make physical computations with much much much more precision than what is physically relevant.
I guess the kind of problems studied using quantum monte carlo where the “sign problem” shows up could give some fairly clean examples of computational physics problems which are hard for classical computers.
http://arxiv.org/abs/cond-mat/0304008
Hi Gil,
recently, I published a paper showing a nonlinearity in quantum mechanics, once that the controlled-NOT gate (CNOT) is mathmaticaly reversible, but does not undo itself in adiabatic constraint. I think if CNOT gate fails, then, quantum computers cannot exist.
http://www.sciencedirect.com/science/article/pii/S0378437114006992
What about Shor’s algorithm?
In other words, CNOT gate only is reversible (gate model works) if the greatest lower bound of entropy is reached (noiseless condiction).
One interesting question coming up from the discussion concerning the magnetic dipole moment of the electron, is what is the optimal accuracy that we can expect from QED computations, assuming that we can carry these computations. Consider the expansion where the kth term corresponds to diagrams with k loops. It is known that eventually the terms will explode but perhaps it can be estimated how many additional terms will still be “tame” and what will be the effect of adding them on the number of relevant digits in the computation. For this purpose we can consider the largest k for which the contribution c(k+1) of the (k+1) term is still much smaller than the contribution of the k th term. (This is a reasonable cut-off.) Estimation (even roughly) this value of k and c(k), may be a feasible combinatorial question. Is it known? (It sounds like something that people must have worked out already.)
Giving (even a heuristic) argument that quantum computers can improve the accuracy of QED estimations for the magnetic dipole moment of the electron from 14 digits to 20, 40 or 100 digits would be quite exciting.
The hope that computations in quantum field theory can be carried our efficiently with quantum computers was (perhaps) one of Feynman’s motivation for QC. I don’t know if it is known that QC will enable to carry out this specific QED computation efficiently but important progress towards quantum algorithms for computations in quantum field theories was achieved in this paper: Stephen Jordan, Keith Lee, and John Preskill Quantum Algorithms for Quantum Field Theories. (I personally know, both Stephen, Keith, and John!)
(A cool exercise in quantum programming 1.2 could be: compute the first 2000 digits of the magnetic dipole moment of the electron as predicted by the first 100 terms of the QED expansion, and then, regarded as a 2000 digits integer, find its prime factorization!)
Aram “…there are a large number of full-time researchers working on lattice QCD who would be delighted to be able to replace their quantum simulations with classical ones.”
Dear Aram, it is kind of interesting to compare what will be the implication on lattice QCD computations (and related physics computation) of the two possibilities we consider: operating quantum computers on the one hand, and a removal of the quantum-supremacy option on the other.
With operating quantum computers, computations from quantum field theory (believed to be computationally intractable on classic computers) could be performed, in real-life, by efficient quantum algorithms. (This was Feynman’s original motivation; there are theorems supporting it but perhaps not in the generality we want.) This means that we can expect quantum computers to perform computations from QED and QCD in much much greater accuracy than we witness today. This will apply to computations related to realistic physics and to computations related to men-made imaginary models alike. If we are lucky we can perform computations related to the fine structure constants or properties of the proton and neutron with hundreds digits accuracy, much beyond anything which is physically relevant. This will be a miracle!
If quantum supremacy will be removed from the table, it will indeed give a reason for optimism that efficient computational methods (on our digital computers) can be developed for describing realistic robust physical processes. Heavy computations will probably still be needed (just like in other sciences without claims of supremacy) for various reasons:
1) Computational shortcuts will require knowing internal parameters of the process which are not available to us (but are available to nature). This can be seen as the learnability-gap in computational complexity. It is computationally hard to learn functions of even low level computational-complexity class.
2) Heavy computations can occur for a model representing a physical process that depends on much more parameters than represented by the input size.
3) An effective efficient model can actually be much more complicated to represent than a simple non-efficient model that agrees with it on physically relevant inputs.
4) And, of course, heavy computation can occur when we simply do not know the correct model or relevant computational tool.
But beside the general sense of optimism regarding classical simulation from removing the quantum supremacy option (in general, or for specific physical areas), it can also lead to specific insights towards efficient computation methods. (In some cases, perhaps familiar ones.)
The very simple BosonSampling story is an example. Assuming a level of noise that will make the computation tractable, immediately leads to an effective computational method (via a small Hilbert space of law-degree polynomials). There are reasons to expect that such a computation method may extend beyond what the mathematical theorem promises. Of course, if you do not know that, you can still compute the noisy BosonSampling using permanents (demonstrating point 4 above). And even if you do know it you can still have the illusion that what nature really does is mixing quantum-superior samples based on permanents.
Let me make it clear that I do not want to belittle the importance, on the conceptual level and on the computational potential alike, of “no-quantum-supremacy.” The whole point of my longish comments outlining 19 or so predictions and describing other possible predictions, connections and applications, (some surely provocative), was precisely to suggest that the no-quantum- supremacy does have a delightful potential for developing an important theory. Not a miracle of a computation device as strong as a computer of the size of the universe running for the life-time of the universe. Not a miracle of efficient hundred-digits accuracy for hard physics computations. But still something to get full-time (and part-time) researchers delighted.
Thanks as always, Klas, for your comment and link.
One speculative question that naturally arise from the discussion as well as from my point G in my second lengthy comment is this:
The same question applies to other physical constants perhaps like the mass of a proton (or the plank constant if you wish).
The question is not if these constant are not constants but varies with time or from one place of the universe to another (that people sometime discuss);
the question is if these constants are really constants, but they are described not by a single real number but by a probability distribution.
Another thing regarding point G in my second lengthy commentabout the nature of fluctuations of interacting systems, coming from the mathematical side, is that in critical systems of statistical mechanics, quantities (like the size of the connected cluster containing the origin, as Itai Benjamini mentioned to me) often have distributions which are “smeared” -the variance behave like square root of the expectation. I am not aware of such quantities that are directly related to fundamental physical constants though.
Let me also mentioned that I asked on TCS stackoverflow some questions that came from our discussion such as the following one:
The question here about the constants being actually probability distributions is a sort of a sharp alternative to a yes answer.
Update: Stephen Jordan gave a detailed answer to my question.
Physics by using boson sampling instead of a full quantum computer
http://arxiv.org/abs/1412.8427
Dear David, thanks! I will certainly look at the paper. Boson sampling is much on my mind recently: Here is the arXiv version of my paper with Guy Kindler on noise sensitivity and BosonSampling, and here is a videotaped presentation given here at HUJI on our work.
There were plenty of interesting discussions and comments I would like to report but let me single out an important development that goes against my conjectures (that Nadav Katz just told me about):A recent paper by the Martinis’ group, State preservation by repetitive error detection in a superconducting quantum circuit, demonstrates that quantum-error correction for a line array of 9 qubits can lead to an improvement by a factor of 8.4 in the coherence time of the logical protected qubit compared to the physical qubits!
Another update is that yesterday we had a workshop here at HUJI entitled “Quantum computer: achievable reality or unrealistic dream organized by Professor Miron Ya Amusia and featuring Nadav and me as speakers. Here are the slides for my lecture: What can we learn from a failure of quantum computers. (In his lecture Nadav mentioned the new work of Martini’s group in connection with my Conjecture 1.4.)
Gil, the attention of readers of Combinatorics and More is directed to a fine essay that appeared on The Quantum Pontiff, by Steve Flammia, titled “Self-correcting fractals”.
Steve’s essay summarizes Courtney Brell’s recent preprint “A proposal for self-correcting stabilizer quantum memories in 3 dimensions (or slightly less)” (arXiv:1411.7046 [quant-ph]). In turn, Brell’s preprint surveys much previous work on quantum error correction in regard to the design and experimental demonstration of large-N long-duration qubit memories.
Steve mentions too, another terrific recent arxiv preprint: “Quantum Memories at Finite Temperature” by Ben Brown, Dan Loss, Jiannis Pachos, Chris Self and James R. Wootton (arXiv:1411.6643 [quant-ph]).
Particularly enjoyable (for me) was the well-balanced survey that these two articles provided, of the literature of increasingly ingenious memory designs, in apposition (not opposition!) to the expanding domain of no-go theorems.
—–
Appreciation Friendly quantum-appreciating weblogs like Combinatorics and More, The Quantum Pontiffs, Gödel’s Lost Letter and P=NP, and Shtetl Optimized gave the quantum community outstanding service in 2014 … researchers like me can only say — like Dicken’s character Oliver Twist — “Please colleagues, we want some more”
Dear John,, I also liked a lot the post by Steve. Here is the link! It is an important question to demonstrate a quantum gadget with similar properties to Kitaev 4D surface code but in dimension 3, and thinking about fractals and fractional dimension is brilliant.
Pingback: Quantum computing: achievable reality or unrealistic dream | Combinatorics and more
Pingback: Why Quantum Computers Cannot Work: The Movie!
Pingback: The Race to Quantum Technologies and Quantum Computers (Useful Links) | Combinatorics and more
Pingback: A toast to Alistair: Two Minutes on Two Great Professional Surprises | Combinatorics and more
Pingback: Quantum Future: Just Beyond Our Grasp - Enterra Solutions