
Rick Wilson
The Frankl-Wilson theorem is a remarkable theorem with many amazing applications. It has several proofs, all based on linear algebra methods (also referred to as dimension arguments). The original proof is based on a careful study of incidence matrices for families of sets. Another proof by Alon, Babai and Suzuki applies the “polynomial method”. I will describe here one variant of the theorem that we will use in connection with the Borsuk Conjecture (It follows a paper by A. Nilli). I will post separately about more general versions, the origin of the result, and various applications. One application about the maximum volume of spherical sets not containing a pair of orthogonal vectors is presented in the next post.
Let and suppose that
is an odd prime.
Theorem: Let be a subset of
with the property that no two vectors in
are orthogonal. Then
.
We will prove a slightly modified version which easily implies the Theorem as we stated it before:
Let be the set of vectors (
) in
such that
and the number of ‘1’ coordinates is even. Let
be a subset of
with the property that no two vectors in
are orthogonal. Then
.
Proof:
The ad-hoc trick:
Claim 1: Let . If
then
.
This is a crucial part of the argument and as far as I can see the part that you need to replace entirely in other applications of the method.
We need
Claim 1′: For every ,
.
Given Claim 1′, if then
. Since the first coordinate is 1 it is not possible that
and it follows that
.
Proof (of Claim1′): Suppose that the number of coordinates where
and
is
, the number of coordineates where
and
is
, the number of coordineates where
and
is
, and the number of coordineates where
and
is
. The inner product
. Now
is even and also
is even so
is also even and
is divisible by 4.
is divisible by 4 and therefore so is
.
The algebra-puzzle trick
Compute .
The answer is ZERO because one of the terms is (x-x).
Magic: underline the empty line with your mouse to see the solution.
Define a family of polynomials in variables
, over the field with
elements
as follows. For every
define
. Here
.
Claim 2: For ,
we have
.
Proof: Since we must have that
for some
,
. Therefore one of the terms in the product defining
must vanish. (Remember, we work over the field with
elements. Ahla!
Claim 3: .
Proof: The inner product of a vector with itself in
. This is important! Therefore
. (It is a product of non-zero numbers modulo
. What is
modulo p? This is a result of a different Wilson.) Walla!
Remark: Some people prefer to simply write which gives a different less extravagant way to present the same thing. (And without the algebra-puzzle.) I still prefer the way we defined the polynomials because for other applications of the method, it generalizes more easily.
The linear algebra (diagonal) trick
Claim 4: The polynomials are linearly independent.
Proof: Suppose that . Substitute in this sum
for
. By Claim 2 we obtain that the outcome is
. By claim 3
and therefore
. Sababa!
Remark: It is worthwhile to remember a variation of this trick, the linear algebra upper-diagonal trick, where you conclude linear independence when you assume that there is some order on your set of ‘s and that
for
.
The multilinearization trick
We now replace the polynomials by new polynomials
by applying the following rule:
Replace each by 1 and each
by
!
Claim 5: The new polynomials are square-free, and they attain the same values for vectors with coordinates .
Proof: This is because when we have a variable that attains only the values +1 and -1 the value of
is 1, and the value of
is the same as that of
. Walla!
Claim 6: The polynomials are linearly independent.
Proof: The proof of claim 4 applies. Walla!
The end of the proof:
By claim 6, the size of is at most the dimension of the vector space of square-free polynomials of degree
in
variables
. This dimension is the number of sqauare-free monomials of degree
in
variables
which is
.
Sababa!

The reason the second version implies the first is as follows: If we flipp the value of the first coordinate we do not change inner products so the second version applies also to subsets of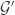 which is the set of all vectors with
which is the set of all vectors with 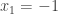 having odd numbers of ‘1’s. The proof only used the fact that the number of 1 coordinates is even and there are no antipodal vectors
having odd numbers of ‘1’s. The proof only used the fact that the number of 1 coordinates is even and there are no antipodal vectors  . Therefore, we can simply cover all
. Therefore, we can simply cover all  vectors by 4 sets to which the second version applies.
vectors by 4 sets to which the second version applies.
Pingback: How Large can a Spherical Set Without Two Orthogonal Vectors Be? « Combinatorics and more
Many thanks for the nice exposition! Here are two questions motivated by it.
1) How sharp the Frankl-Wilson estimate is? *not* of the form
*not* of the form  with
with  prime?
prime?
2) What is the estimate for
Thanks! 1) If you look at the set of all the vectors with at most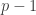 ‘-1’s or at most
‘-1’s or at most 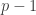 +1’s you get an example with no two orthogonal vectors, with about half the number in the theorem. 2) If n is even but not of the form we considered you can apply Frankl-Rodl’s theorem to get bounds of the form
+1’s you get an example with no two orthogonal vectors, with about half the number in the theorem. 2) If n is even but not of the form we considered you can apply Frankl-Rodl’s theorem to get bounds of the form  with worth value of
with worth value of  . (The Frankl Wilson theorem gives the correct value of
. (The Frankl Wilson theorem gives the correct value of  in the four times prime case.)
in the four times prime case.)
Pingback: Borsuk’s Conjecture « Combinatorics and more
Pingback: Four Derandomization Problems « Combinatorics and more
Pingback: Combinatorics and More – Greatest Hits | Combinatorics and more
Dear Prof. Gil Kalai,
Is Claim 1 correct? If I take p = 2, n = 4×2 = 8. Let x = (1,1,1,1,-1,-1,-1,-1), y = (1,-1,1,1,1,-1,-1,-1), then = 0 mod 2 but =6 mod 8, a contradiction.
Dear Prof. Gil Kalai,
Is Claim 1 correct? If I take p = 2, n = 4×2 = 8. Let x = (1,1,1,1,-1,-1,-1,-1), y = (1,-1,1,1,1,-1,-1,-1), then $ = 0$ (mod 2) but $=4$ (mod 8), a contradiction.
Right, it is always the case that = 0 (mod p) but for being 0 (mod 4p) we need that p is an odd prime. Corrected. Thanks.
Yes, number 2 is only the even prime. I think it’s better to say p>2.
Dear Prof. Gil Karai,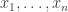 which is
which is 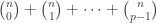 .”
.”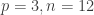 , square-free monomials of degree 2 in 12 variables are
, square-free monomials of degree 2 in 12 variables are  , hence there are 13 square-free monomials in 12 variables. BUT your answer is
, hence there are 13 square-free monomials in 12 variables. BUT your answer is  . Could you please explain?
. Could you please explain?
I really don’t understand your argument at the end of the proof : “number of square-free monomials of degree p-1 in n variables
For example,
Many thanks,
Dear dvhoan, The square free monomials are 1, ,
, 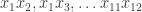 . So for every subset of {1,2,…,12} of size 0, 1, 2 we have a monomial which is the product of variables with indices in the subset.
. So for every subset of {1,2,…,12} of size 0, 1, 2 we have a monomial which is the product of variables with indices in the subset.
Dear Prof. Gil Kalai, I understand now. Thank you so much for your nice explanation.
Pingback: Updates and plans III. | Combinatorics and more
Pingback: Difference sets missing a Hamming sphere | Quomodocumque
Pingback: Basic Notions Seminar is Back! Helly Type Theorems and the Cascade Conjecture | Combinatorics and more
Pingback: Peter Keevash and Eoin Long: Forbidden vector-valued intersections | Combinatorics and more
Pingback: Extremal Combinatorics V: POSETS | Combinatorics and more
Dear GIl,
I just stumbled upon this old post. Some time ago, Hajime Tanaka and I noticed that you can slightly modify the argument for n being an even prime power. The trick is to divide by 2 at one point. Then the proof works for all prime powers n, not just the odd ones.
(In the note we have n an even prime power, but there is no need.)
https://arxiv.org/abs/1901.04860