This post is based on a comment by Oz to our question about balls with two colors:
“There is an interesting (and more difficult) variation I once heard but can’t recall where:
You have a box with n red balls and n blue balls. You take out each time a ball at random as before. But, if the ball was red, you put it back in the box and take out a blue ball. If the ball was blue, you put it back in the box and take out a red ball.
You keep as before until left only with balls of the same color. How many balls will be left (as a function of n)?
1) Roughly εn for some ε>0.
2) Roughly 
3) Roughly log n?
4) Roughly a constant?
5) Some other behavior
Combinatorics and more 
I’m fairly sure that there is not enough bias to get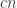
, but it intuitively seems far too much bias to still be 
. I want to say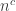 
. At a wild guess, it’s either 
or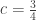 
, since those are the simplest exponents between 
and 
.
Wow! that’s a bold guess, Peter! (I don’t know the answer myself.)
Here’s a very hand-wavy reason you might expect about $n^{3/4}$. Suppose that (say) there’s $R$ red balls and $B$ blue balls, and $R>B$. Then the advantage to red at the next step is proportional to $(R-B)/(R+B)$.
Now imagine that the whole process is scaled to take place over the interval $[0,2]$ (so that each draw takes time $1/n$), and let $f(t)$ be $1/n$ times the absolute difference $R-B$ at time $t$. Since $R+B=(2-t)n$, we can think of the above advantage as being akin to a differential equation that holds on average: $f'(t) \sim \frac{f(t)}{2-t}$.
There’s still some weirdness at the ends. For $t$ close to $1$ this breaks down because $R-B$ can’t change by more than $1$ with each draw (effectively bounding $f'(t)$ by $1$), and for $t$ close to $0$ the dominant part is the random fluctuations rather than the existing bias.
But maybe we could take $f(0) \approx n^{-1/2}$ to account for the bias, and stop when $f'(t)=1$ (i.e. $f(t)=2-t$) to represent that then one side’s essentially already won. In this case the solution is $f(t)=\frac{1}{\sqrt{n}(2-t)}$, and the stop is at $t=2-n^{-1/4}$, corresponding to $n^{3/4}$ balls remaining of one color.
After a short numerical simulation (start with 100k balls total for k between [1,100], average over 10,000 tries at each k) I have the following fit:
log(# balls left) = 0.068 + 0.748 log(# balls to start)
Dear Lior, this certainly looks like 3/4!
A few years ago I asked Tom Bohman about an equivalent question. As far as I remember, he claimed that the answer is $C n^{3/4}$ where $C$ is not concentrated at a single value, but is distributed according to a distribution that is supported on all of $\mathbb{R}^+$. He might know more.
Dear Boris, we just had our 4th Student probability day last week and Yuval Peres told me what and where the answer to Oz’ question are. I will write about it soon.
There are probably good reasons for all the $n^{3/4}$ answers so I’d vote for that based on majority rules. BUT if I was answering it myself then I would make a wild guess of $O(n^{1/2}).$ for reasons given below.
Note that there is an easy recurrence so the problem can be solved numerically for any fixed n. Call the case of r red out of t total balls (r,t) and let a(r,t) be the expected number of balls left when we arrive at (0,a) (by convention swap the colors when needed to maintain 2r<=t) then we move from (r,t) to either (r,t-1) or (r-1,t-1) with probabilities r/t and (1-r/t) respectively.
The ODE dr/dt=1-r/t seems relevant. An initial condition of r(2n)=n is no help but we do know that the first step (up to color switch) takes us from (n,2n) to (n-1,2n-1) and with that as an initial condition I get r(t)=(t^2-2n+1)(2t). Then solving r(t)=0 for t yields $\sqrt{2n-1}.$ The numerical data does seem higher than this though.
As I final note, this reminds me of the amazing article The Toilet Paper problem by Donald Knuth October 1984 in the American Mathematical monthly http://www.jstor.org/stable/2322567.
Two kinds of people, one who always removes the majority color and one who always removes the minority color are represented in ratio p:1-p If we start out with n of each color , how many will be left when one color is depleted? I was mildly scandalized that the problem story involves big choosers and little choosers who take a square of toilet paper from one of two available rolls in a certain stall. So that's what they mean by applied math! The math is breathtaking as well and maybe there are ideas to exploit.
make that (t^2-2n+1)/(2t)
Since a(200,400)=55.603 and $200^{3/4}=53.183$ (and similar results) $n^{3/4}$ looks pretty believable.
This problem was solved by Kingman at the University of Bristol, UK. http://www.maths.bris.ac.uk/research/stats/reports/2001/0124.pdf in 1999 has a summary and improvements/extensions.
http://mathoverflow.net/questions/130845/blue-and-red-balls-puzzle
There is a simple martingale argument which shows that if there is a scaling law as n^c, then c=3/4. I don’t think this is in the paper noah links, although that has some other nice ideas and precise results.
Suppose that when there are r red balls and b blue balls, you bet r to win b that you will remove a blue ball next. The total value accumulated from (n,n) to (r,b) does not depend on the path. You must have lost n, n-1, …, n-r+1 and won n, n-1, …, n-b+1. If you end up with k balls, you have accumulated +-k(k+1)/2.
When you make a fair bet of r to win b, this contributes rb to the variance. The total variance is between roughly (1/2)n^3 (winning n times straight) and (2/3)n^3 (alternating wins and losses). If you end up at roughly +-n^c(n^c+1)/2, and the variance is proportional to n^3, then 4c=3, and c=3/4.
Pingback: Weekly links for May 20 | God plays dice
Pingback: Another Interesting Ingredient « The Epsilon Tale