Ladies and gentlemen, a conference celebrating Noga Alon’s 60th birthday is coming on January. It will take place at Tel Aviv University on January 17-21. Here is the event webpage. Don’t miss the event !
Cash Prizes!
The poster includes 15 formulas representing some of Noga’s works. Can you identify them?
The first commentator to identify a formula will win a prize of 10 Israeli Shekels (ILS) that can be claimed on Noga’s Fest itself, (or else, in person, next time we meet after the meeting.) Cash prizes claimed in person on the meeting will be doubled! Cash prizes for the oldest and newest formulas are tripled! There is a limit of one answer/prize per person/ per week. Answers need to include the formula itself, tell what the formula is, and give crucial details about it.
More cash prizes!!
For each of these formulas, once identified, the comment giving the latest place where the formula is reproduced, (in a later paper or book not coauthored by any of the original discoverers) will be eligible also to 5 ILS prize. The same doubling and tripling rules as above apply. Here there is no limit on answers per person.
And even more cash prizes !!!
There will be 5 additional prizes of 20 ILS for formulas by Noga, that did not make it to the poster. Same doubling and tripling rules apply.
And Even More! Win a Travel Grant to the conference
Among all participants who are students or post docs, one grant for a round trip to the meeting will be given.
Rules
People involved in preparing the poster are not eligible.
The competition opens now!!!
And here are more details on the meeting itself. (The meeting also celebrates a decade anniversary for Zeilberger’s Opinion 71.)
INVITED SPEAKERS
- Béla Bollobás – University of Cambridge
- Jennifer Chayes – Microsoft Research
- Uri Feige – Weizmann Institute
- Jacob Fox – Stanford University
- Péter Frankl – Alfréd Rényi Inst. of Math
- Zoltán Füredi – Alfréd Rényi Inst. of Math
- Shafi Goldwasser – MIT and Weizmann Institute
- Gil Kalai – Hebrew University
- Nati Linial – Hebrew University
- László Lovász – Eötvös Loránd University
- Vitali Milman – Tel Aviv University
- Assaf Naor – Princeton University
- Jaroslav Nešetřil – Charles University
- János Pach – EPFL
- Yuval Peres – Microsoft Research
- Vojtěch Rödl – Emory University
- Peter Sarnak – Princeton University and IAS
- Alexander Schrijver – CWI Amsterdam
- Micha Sharir – Tel Aviv University
- Saharon Shelah – Hebrew/Rutgers University
- Joel Spencer – NYU
- Endre Szemerédi – Alfréd Rényi Inst. of Math
- Terence Tao – UCLA
- Moshe Tennenholtz – Technion
- Avi Wigderson – IAS
- Tamar Ziegler – Hebrew University
ORGANIZING COMMITTEE
- Yossi Azar – Tel Aviv University
- Michael Krivelevich – Tel Aviv University
- Asaf Shapira – Tel Aviv University
- Benny Sudakov – ETH Zurich
- Uri Zwick – Tel Aviv University
Combinatorics and more 
The third formula from the left
is the "discrete Cheeger-Buser inequality", relating the spectral gap of the discrete laplace operator to the discrete Cheeger constant of a graph… In particular, it gives the spectral characterization of expander families.
The fourth formula is a bound on the linear arboricity la(G) of a graph G of maximum degree d from a paper published in 1988. The linear arboricity of a graph is the least number of parts of a partition of the edges of the graph so that each part induces a forest of paths. The bound is an asymptotic verification of the linear arboricity conjecture due to Akiyama, Exoo and Harary in 1980.
To comply with the rules, the bound is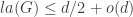
and it is a classic application of the probabilistic method, using in particular the Lovász Local Lemma.
The last formula on the left is the Alon–Boppana bound, showing that the spectral gap of the regular tree is essentially best possible for large regular graphs.
To comply with the rules, the Alon–Boppana bound appears above as
(though the error term can be made quantitative). The claim is that the second largest eigenvalue of (the adjacency matrix of) a large $d$-regular graph $G$ (following the “trivial” eigenvalue 
) cannot be much smaller than 
, the spectral radius of the universal covering tree, with an error term that goes to zero as the number of vertices goes to infinity. The proof is by connecting the trace of a large power of the adjacency matrix of a count of paths in the graph, and comparing counts in the graph and in the tree.
The 9-th formula from the top is a lower bound on the size of the “restricted sum” of sets A and B, which is {a+b| a \in A, b \in B, a \ne b}. It is a beautiful application of the combinatorial nullstellensatz.
The Alon–Boppana bound is reproduced in Bordenave’s paper giving a new proof of Alon’s conjecture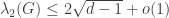
for random 
-regular graphs (I enter this into the “other formula” list). See arXiv:math.CO/1502.04482.
The second last formula \(R(C_4,C_4,C_4,K_m) = \Theta(m/\log^2 m)\) is an asymptotically tight bound on the multicolored Ramsey number for \(C_4, C_4, C_4, K_m\), which is the smallest integer r such that any edge coloring of \(K_r\) using 4 colors either has a monochromatic \(C_4\) in colors 1,2, or 3, or a monochromatic \(K_m\) using color 4.
Shouldn’t the exponent in the seventh formula be $2-1/s$ rather than $1-1/s$ ?
Let me add more details. I am referring to the formula
. This is a special case of the Zarankiewicz problem. The problem asks for the maximum number of edges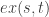 
in a bipartite graph with 
vertices and no 
as a subgraph. The bound 
is known already from the 1950’s. However, so far it was proven to be tight only for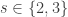 
. Alon, Rónyai, and Szabó proved the bound 
. I hope that this is what the formula is indeed referring to.
Oops. My formulation was a bit messy. I of course meant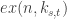
rather than 
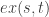. So the formula should be $latex ex(n,k_{s,(s-1)!+1})=\Omega(n^{2-1/s}).
10-th formula appeared in the paper “The 123 Theorem and its extensions” (with R. Yuster).
The paper stated that for two independent and identically distributed random variables X,Y the formula P(|X-Y|<2) <= 3Prob(|X-Y|<1) holds.
The proof of the theorem (actually, a general version of it) is based in a very simple and nice combinatorial argument.
The crucial fact is that the constant 3 in the theorem is the best possible constant and it can be checked by considering the uniform random variable in the set {0,2,…,2n}
The second from the left is a formula for the off-diagonal Ramsey number
. This is from a beautiful paper of Noga and Vojta Rödl which shows how to prove tight bounds on many different off-diagonal Ramsey numbers.
The third formula from the top, APSP(n) <= n^((3+omega)/2), is from Alon's paper "On the Exponent of the All Pairs Shortest Path Problem" with Galil and Margalit. They give an algorithm yielding an upper bound of (3+omega)/2 < 2.688 for the exponent of the APSP problem when the edge weights are integers bounded in magnitude by a constant M. This improves on the exponent of 3 from the Floyd-Warshall algorithm.
I believe the first formula is from a paper with Seymour and Thomas on a generalisation of Lipton and Tarjan’s separator theorem to non-planar graphs — they show that a graph with no
-minor has a separation of order at most 
,
The fifth formula from the bottom
edges. This is a theorem in Noga’s very first publication http://www.tau.ac.il/~nogaa/PDFS/publications.html
gives the maximum number of copies of a fixed graph H in a graph with
Dear Emmanuel, Ross, Lior, Shachar, Sushant, Adam, Nicolas, David, Josh, Bhargav, and Yufei, Many thanks for your answers!
The second formula, \(F(n,\sigma) \leq c^{n \gamma^* (n)} \), is from a 2002 paper with Ehud Friedgut “On the Number of Permutations Avoiding a Given Pattern”. For a fixed permutation \(\sigma \in S_k\) the formula provides an upper bound on the number of permutations in \(S_n\) avoiding \(\sigma\). This formula is a weaker version of a conjecture of Stanley and Wilf.
OK, without me being familiar with the blogosphere I mistakenly posted my comments on Gil’s FB wall. So now its late for some formulas and my dream of a new Mercedes is how to say …… lost . So let me try a new one:
The 5’th formula is an upper bound on the number of directed Hamiltonian paths in a tournament on $n$ vertices from this paper of Noga: http://www.tau.ac.il/~nogaa/PDFS/hamilton.pdf
Pingback: Updates and plans III. | Combinatorics and more
The fourth inequality from the bottom is another equation by Alon and Boppana, which appears in this paper (see, i.e., Theorem 3.9): http://www.math.tau.ac.il/~nogaa/PDFS/Publications/The%20monotone%20circuit%20complexity%20of%20Boolean%20functions.pdf
It provides a lower bound on the monotone circuit complexity of determining if a graph with
edges contains a clique of size 
. This strengthens a previous result by Razborov, in particular, giving an exponential lower bound for a particular choice of 
(whereas Razborov’s result only provided a super polynomial lower bound).
And for completeness, the formula itself is
.
The 6th formula appears in a 1998 paper on Shannon capacity of graphs (http://link.springer.com/article/10.1007%2FPL00009824), where he showed there exist graph pairs G, H with Shannon capacities at most k such that the Shannon capacity of their disjoint union was much larger than 2k. In particular, he showed you could have H=\bar{G} and Shannon capacity as given in the formula.
The fifth formula
is from Alon’s 1990 paper “The maximum number of hamiltonian paths in tournaments.”
I noticed too late that the sixth formula is already identified, so I will leave my interpretation of the crucial details about it for fun. But let me compete with the latest place where the formula is reproduced.
The sixth formula is from the paper titled “The Shannon Capacity of a union” in Combinatorica 18 (3) 1998. The formula disproves a conjecture of Shannon, namely that the Shannon capacity is subadditive with respect to the disjoint union of graphs. In the paper it is proved that there is a graph G such that both G and its complement has Shannon capacity at most k, and the formula holds. Thus the disjoint union of two graphs can have superpolinomially larger capacity than the original graphs. The argument uses explicit construction, the graph is a Kneser-style graph with 3 parameters:G(r,s,p). The vertices are subsets of size s from [r], and two such subsets are connected iff their intersection is of size -1 modulo p. The proof that the graph satisfies the formula involves both number theory and linear algebra.
The latest independent place where the formula (not the result) itself is reproduced might be the survey “Ramsey Theory Applications” by Vera Rosta. The formula appears on the lower half of page 14. The survey is a dynamic one, and it is last modified in 2004, so there might be room for improvement, unless the author modifies it in the near future. (this fortunate event is unlikely to happen, and I do not plan to take any steps towards it 🙂 )
The 8-th formula comes from Noga’s paper “Bipartite subgraphs” Combinatorica 16 (1996) and involves f(e) which is the the largest integer such that any graph with e edges contains a bipartite subgraph with at least f(e) edges.
Pingback: Important formulas in Combinatorics | Combinatorics and more
I fear that I will be slightly off here, but the 7th formula looks like a simplified version of Theorem 9 of “Norm graphs: variations and applications”, where a bound on the Turan number for the complete bipartite graph $$K_{t, s}$$ with $$s > (t-1)!$$. The expression $$ex(n, K_{n, n!})$$ denotes the maximum number of edges in a graph with $$n$$ vertices that does not contain a copy of $$K_{n, n!}$$.
Two remarks:
– I think that it should be $$n^{2-1/s}$$, not $$n^{1-1/s}$$. That is what is in their paper and it is a better bound.
– The $$C$$ depends on $$s$$.
I tried to find a paper with $$n^{1-1/s}$$ or where $$C$$ does not depend on $$s$$, but I could not. Anyway, this was (to my knowledge) the important paper.
And I looked up the wrong reference for LaTeX with WordPress …
I forgot to mention the co-authors of the paper: Lajos Rónyai and Tibor Szabó.
If someone remind me, how to do LaTeX in WordPress, then I will correct my post.
Pingback: The (Random) Matrix and more | Combinatorics and more
Pingback: Important formulas in combinatorics – Math Solution
Pingback: Greatest Hits 2015-2022, Part I | Combinatorics and more