A quote from a recent post from Jordan Ellenberg‘s blog Quomodocumque:
Briefly: it seems to me that the idea of the Croot-Lev-Pach paper I posted about yesterday (GK: see also my last post) can indeed be used to give a new bound on the size of subsets of F_3^n with no three-term arithmetic progression! Such a set has size at most (2.756)^n. (There’s actually a closed form for the constant, I think, but I haven’t written it down yet.)
Here’s the preprint. It’s very short. I’ll post this to the arXiv in a day or two, assuming I (or you) don’t find anything wrong with it, so comment if you have comments!
This is amazing! The cap set problem was quite popular here on the blog, see also Tao’s 2007 post, and Jordan made also quite an effort over the years in proving the other direction before proving this direction. (Fortunately for our profession, success for two conflicting statements was avoided.) Congratulations to Jordan, Ernie, Seva, and Peter!
Update: Congratulations also to Dion Gijswijt who also derived a similar solution to the cap set problem based on CLP! See this comment on Quomodocumque.
Updates: See also this post by Tao (presenting a symmetric version of the proof), this post by Gowers, this post in by Luca Trevisan, and this post by Peter Cameron, and this post by Anurag Bishnoi. See also this lovely quanta article Set proof stuns mathematicians by Erica Klarreich. See also the post Polynomial prestidigitation on GLL. There, among other things the relation to Smolensky’s early use of the “halving degree trick” for the polynomial method is noted. (See also this comment.)
Of course, there is also plenty of more to desire: Full affine lines for 
Noga Alon also pointed out that the solution of the cap set problem also settles affirmatively the Erdos-Szemeredi weaker version of the Erdos-Rado Delta-system conjecture (via the connections discussed in this post) and also shows that a certain direction for showing that ω=2 for matrix multiplication cannot possibly work. The Erdos-Rado sunflower conjecture is still (at least for a few days) open.
Can the affine results be applied for integers or for combinatorial setting? The geometries are quite different but still… This is of great interest here (and also for other problems like the Kakeya problem). Starting from a positive density set in 
More updates: Eric Naslund and Will Sawin gave a direct proof based on the polynomial method for the Erdos-Szemeredi sunflower conjecture, and an even stronger result is given by Naslund here. (Eric also has stronger quantitative bounds for Erdos-Szemeredi based on bounds for cap sets.) Ben Green has studied the analogue of Sarkozy’s theorem in function fields (other results on function fields are mentioned by Bloom in this comment); Variants on the CLPEG-arguments are described by Petrov and by Bishnoi over the comment threads here and here. Here is a paper by Jonah Blasiak, Thomas Church, Henry Cohn, Joshua A. Grochow, Chris Umans, on consequences of the cap set result for fast matrix multiplication.
More updates (May 31): New applications are mentioned in a new post on quomodocumque: sumsets and sumsets of subsets including a lovely new application by Jordan, a link to a paper by Robert Kleinberg: A nearly tight upper bound on tri-colored sum-free sets in characteristic 2. And here is a link to a new manuscript by Fedor Petrov Many Zero Divisors in a Group Ring Imply Bounds on Progression–Free Subsets.
One more: (Quoting Arnab Bhattacharyya, June 15 2016 on GLL) Another amazing result that follows from these techniques for one of my favorite problems: http://arxiv.org/pdf/1606.01230v2.pdf. Fox and LM Lovasz improve the bounds for the arithmetic triangle removal lemma dramatically, from a tower of two’s to polynomial!
More (Early July 2016) : An interesting new post on Ellenberg’s blog.
Combinatorics and more 
I just want to recall that the weak sunflower conjecture is implied by a good bound on $R_r(k)$ as well as we discussed in [1]. So instead of the strong sunflower conjecture this is a second problem that one might want to think about in this context.
[1] https://gilkalai.wordpress.com/2016/01/31/polymath10-post-4-back-to-the-drawing-board/
Excuse me, I was slightly confused. The weak sunflower conjecture is of course not the conjecture for weak Erdos-Rado Delta-system, but just something different. My bad.
All this array (zoo?) of conjectures is very confusing!
Perhaps it should be noted that the upper bounds obtained by both Jordan and Dion are the same. They both prove that the size of a 3-term progression free set in F_q^n is bounded above by the total number of monomials of degree at most (q – 1)n/3 in which each variable has degree at most q – 1, i.e., the number of integral solutions of, e_1 + e_2 + … + e_n <= (q – 1)n/3, 0 <= e_i <= q – 1. Since we know this now, may be we can find alternate ways of proving their result, which could shed some more light on other related problems.
Dear Anurag, Finding alternative proofs to other applications of the polynomial method is very often not known and always quite tricky. What I am most curious about is if “the total number of monomials of degree at most (q – 1)n/3 in which each variable has degree at most q – 1,” (a) does not hide some unpleasant constants depending on q, and (b) suffices to derive a Behrend-type upper bound for Roth numbers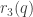
.
(Namely: to (strangely) deduce a Behrend type bound for n=1 from the assymptotic result as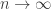
.)
Added later: Apparently, as the experts expected, the new bounds have no baring on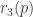
.
Let me mention that one important case where an alternative method is known is the Frankl Rodl theorem (extending the Frankl-Wilson theorem which uses the polynomial method but via a different technique). At some earlier posts we related these results to some weaker versions of the cap set problem.
There is one case of the polynomial method, namely that of the Frankl Wilson theorem where an alternative proof (with less optimal but qualitativly similar bounds) was found by Frankl and Rodl. Moreover the Frankl-Rodl bound applies in much greater generality. In some posts here in 2009 I described and discussed (part I, part II, part III) an idea to use the polynomial method for a weak version of the cap set problem and at that time applying the very general form of Frankl-Rodl (for which no proof via the polynomial methods are known) gave the best results.
Dear Gil, thanks for pointing out the Frankl-Rodl theorem. But I wasn’t just thinking about non-polynomial method proofs when I said alternate proofs. Proofs that use polynomials in a different way might also shed some light. For example, see this alternate proof by Fedor Petrov: https://dl.dropboxusercontent.com/u/15433464/f3_eng.pdf, https://terrytao.wordpress.com/2016/05/18/a-symmetric-formulation-of-the-croot-lev-pach-ellenberg-gijswijt-capset-bound/#comment-468759. It seems quite different from the proofs of Ellenberg-Gijswijt, and it improves the constant in the bound.
Concerning full affine lines for $q>3$: is anything at all known on it?
Aren’t those simply the complement of affine blocking sets? Assuming that you are talking about subsets of F_q^n which do not contain any affine line. For affine blocking sets, not much is known. See this and the references therein, http://mathoverflow.net/questions/229417/blocking-sets-in-three-dimensional-finite-affine-spaces.
They are. I am aware of that your MO question; the difference is that your question deals with F_q^3, while I wonder what happens in F_q^n for q fixed and n large.
In the literature on blocking sets for lines of affine spaces AG(n, q) I am only aware of the lower bound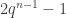
. See [1]. So this implies 
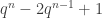as an upper bound for no full lines.
I spend a few minutes to look for papers, which cited on of the papers with the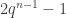
bound, but I could not find any improvements.
[1] P. Sziklai, Nuclei of pointsets in PG(n, q), http://www.sciencedirect.com/science/article/pii/S0012365X97803354
Dear Seva, I think that Furstenberg and Katznelson established a density result for affine lines early on and later established the stronger density Hales Jewett. I am not sure what the best current bounds are for all these questions. It is possible that
points in 
suffices for a full affine line but I am not sure about it.
Well, (q-\epsilon)^n would imply a solution of the capset problem (because any full line contains an arithmetic progression, an indeed lots of them for q large)…
Yes, this would certainly be a major strengthening. But I dont know for fixed q of a counterexample.
Pingback: Polymath 10 Emergency Post 5: The Erdos-Szemeredi Sunflower Conjecture is Now Proven. | Combinatorics and more
Pingback: The new bound on cap sets | Anurag's Math Blog
Pingback: Polymath 10 post 6: The Erdos-Rado sunflower conjecture, and the Turan (4,3) problem: homological approaches. | Combinatorics and more
I have been reading up on Davenport constants and related things recently, and it seems like the link between cap sets and the so-called Erdos-Ginzburg-Ziv constant has not been mentioned in any of the blog posts. Of course, many people might know about this already. Still, here it is. For an abelian group
, let 
be the smallest integer 
for which every sequence of length 
of elements of 
contains a subsequence of length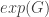 
which sums up to zero. For the case when 
, and thus 
, we have that the maximal size of a cap is equal to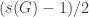 
, and thus we get an upper bound on 
. See this paper: http://imsc.uni-graz.at/geroldinger/56-zero-sum-caps.pdf, or Section 12 of this paper: https://www.mathi.uni-heidelberg.de/~yves/Papers/CapSurvey.pdf.
A new paper by Fox and Sauermann gives a bound on
in terms of 
for prime divisors 
of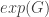 
: https://arxiv.org/abs/1708.09100. This establishes the link between cap sets and EGZ constant in general, while the one I mentioned above was specific to the case of 
.
Pingback: Notes of the seminar ‘On the slice rank of functions’ | Points And Lines
Pingback: Peter Keevash and Eoin Long: Forbidden vector-valued intersections | Combinatorics and more
Here is a very very nice presentation by Dr. Z. https://arxiv.org/abs/1607.01804
Pingback: To cheer you up in difficult times 7: Bloom and Sisask just broke the logarithm barrier for Roth’s theorem! | Combinatorics and more
Pingback: Péter Pál Pach and Richárd Palincza: a Glimpse Beyond the Horizon | Combinatorics and more
Pingback: Barnabás Janzer: Rotation inside convex Kakeya sets | Combinatorics and more
Pingback: Greatest Hits 2015-2022, Part I | Combinatorics and more