While slowly writing Post 5 (now planned to be Post 6) of our polymath10 project on the Erdos-Rado sunflower conjecture, the very recent proof (see this post) that cap sets have exponentially small density has changed matters greatly! It implies a weaker version of the Erdos-Rado sunflower conjecture made by Erdos and Szemeredi. Let me remind the readers what these conjectures are:
The Erdos-Szemeredi Sunflower Conjecture: There is 
The strong Cap Set Conjecture: There is 
Results by Erdos and Szemeredi give that the Erdos Rado sunflower conjecture implies the Erdos-Szemeredi sunflower conjecture. This implication is Theorem 2.3 in the paper On sunflowers and matrix multiplication by Noga Alon, Amir Shpilka, and Christopher Umans where many implications between various related conjectures are discussed (we discussed it in this post). One implication by Noga, Amir and Chris is that the strong cap set Conjecture implies the Erdos-Szemeredi sunflower conjecture!
In order that the post with the cap set startling news will remain prominent, I will put the rest of this post under the fold.
We also refer the readers again to Kostochka’s review paper Extremal problem on Δ-systems, and to the paper Group-theoretic algorithms for matrix multiplication, by Henry Cohn, Robert Kleinberg, Balasz Szegedy, and Christopher Umans.
A few days ago the cap set conjecture was proved (with the upper bound 
Thus, currently the most promising line of attack to the Erdos-Rado sunflower conjecture may well be through the result and methods involved in the Erdos-Szemeredi sunflower conjecture (now theorem) via the strong cap set conjecture (now theorem). Although I don’t have much to say about it myself, discussing this avenue is certainly welcome.
Some questions that come to mind are:
- Can the polynomial method apply also to the full Erdos-Rado sunflower conjecture (for three petals).
- Is there a direct proof (via the polynomial method) for the Erdos Szemeredi conjecture
- Do the new upper bounds for the Erdos-Szemeredi conjecture have some consequences for the Erdos-Rado conjecture?
- What about the Erdos-Szemeredi conjecture for avoiding sunflowers with r petals r>3.
In my next polymath10 post I do plan to return to the homological approach and related technology that I also like for other reasons/problems.
An off topic remark: In the previous post I expressed the (rather obvious) thought that the new cap set development may reflect also on bounds for Roth’s theorem, (little in the spirit of polymath6: “A is to B as C is to ???” ) with some naive thoughts about it. I still hope for some serious discussion about such a possibility.
For a presentation (with some nice modification – the three points on the affine line are treated symmetrically) of the Croot-Lev-Pach-Ellenberg-Gijswijt capset and further discussion see this post and comment thread on Terry Tao’s blog.
Update: Eric Naslund and Will Sawin gave a direct proof based on the polynomial method for the Erdos-Szemeredi sunflower conjecture (for three petals), and an even stronger result is given by Naslund here. I will try to give more updates on applications of the Croot-Lev-Pach-Ellenberg-Gijswijt breakthrough at the end of this post.
Combinatorics and more 
Gil, I have been thinking about two questions which I think are related to your previous post. 1. Can the Croot-Lev-Pach method be used for arithmetic progressions of length 4 and greater? 2. (Your question from the previous post) Can the method be used for the integers? It seems to me that both applications are obstructed by the same thing. Croot-Lev-Pach works through a lemma that controls for a particular polynomial P of degree d with P(x+y)=0 for every x in X, the number of points in X where P(x+x) is nonzero. This works by look at P(x+y) as an inner product between a vector representing x and a vector representing y. Then when P(x+y)=0, it means that the vectors are orthogonal and when P(x+x) is nonzero, it means they are nondegenerate. Thus one gets a lower bound on the dimension of their span. Let’s say we want to use the same theory for arithmetic progressions of length 4. Then instead of the condition P(x+y)=0, we should get something like for every x and y distinct either P(x+y) or P(x+2y) is zero. (My coefficients are not quite correct, but
this has to do with requiring that for x,y distinct, an AP of length 4 which they start is not contained in the set.) So what we have is a kind of Van der Waerden version of orthogonality. Can we use it to get lower bounds for dimensions? I feel a little hope, but I don’t know how. How about the integers? How could we make the same method work for Roth in the integers? Aside: I find integer addition to be really complicated. I propose studying a simplified model, but not as simple as F_p^n. For the purpose of exposition, I will pretend that 10 is a prime. The difficulty with integer addition is exhibited by the fact that 999+1=1000. In finite fields, 999+1= 990. I propose we study a model where 999+1=900. In this model, when we add two integers in p-ary expansion:
a_1 a_2 … a_d + c_1 c_2 … c_d, we get as the jth digit, a_j+ c_j + b(a_{j+1},c_{j+1}).
Here b is the map from pairs of integers between 0 and p-1 to {0,1} which gives 0 if the sum is less p and 1 otherwise. A simple way to describing this model of addition to a grade schooler is that when we add, we carry 1’s but our carrying at each digit is independent. (No iterative carrying.)
What is the virtue of this model? In the case of F_p^d addition, there is an exponentially small chance in d, that a pair of vectors has the same sum as the corresponding pair of integers. In this model, for the sums to mismatch, there has to be a digit where the sum a_j+c_j=p-1. This has probability only d/p. Pairs where the sum mismatches are as rare as points of the Behrend example, that is codimension 1. So if we could do something for Roth’s theorem in this model, it seems we could do something in the integers too. Now how does this model relate to Croot-Lev-Pach? I want my polynomial P to be over F_p. So the thing which is zero is P(a+c + b(a,c)_shift).
In other words, there is a set of d-1 switches which determines the addition. For a fixed value of these switches, Croot-Lev-Pach would work fine. The question is can we do something when we know that for each a and c, there is a choice among 2^{d-1} inner products which is zero. Do we have a working substitute for Gram-Schmidt in that setting. It’s rather similar to the difficulty with long arithmetic progressions. Do you think there is any hope? Nets
Dear Nets, many thanks for the comment. I am traveling now to a conference so I will think about it only in a couple of days but I hope other people will.
Dear Gil, this is why serious discussions are difficult. Nets
I suppose your comment is already serious compared to my naïve thought that the results for
will miraculously give Behrand-quality lower bounds for Roth. (In fact, I dont see how to get any bound for Roth.) All the points you raise are excellent and certainly it is important to think about length 4. I like the idea of simplified addition.
Regarding of getting the bound on the dimension when either P(2x+y) or P(x+2y) is zero: it is possible, but the bound is too poor. Namely, if we consider the matrices M1={P(2x+y)}_{x,y} and M2={P(x+2y)}_{x,y}, then these matrices have the property that the diagonals entries are equal to 1 and M1_{ij}*M2_{ij}=0 for the off-diagonal elements. A standard argument (see, for example, Lemma 10 in http://arxiv.org/pdf/1508.00145) shows that rank(M1*M2)5.
Hm… My post was cut short (I think the WordPress did not like “less-than” sign). Here is the end of the post:
… shows that rank(M1*M2) is at most rank(M1)rank(M2) where * denotes the entry-wise product. Since the entry-wise product of M1 and M2 is the identity matrix, this gives us the bound of m_{d/2}^2 instead of m_{d/2} in Proposition 1 of Jordan’s write-up. Sadly, that is too weak even in Z_5^n since in that case m_n is approximately 3.8^n (if my calculations are right), and 3.8^2>5.
Probably an easier problem than 4-APs, which is still not obvious, is the corner problem. Namely, can we prove that a corner-free subset of F_p^n x F_p^n has exponentially small density? Here “corner” has the usual for this subject meaning: it is a triple of elements of the form {(x,y), (x+d,y), (x,y+d)}.
I had thought the same and was thinking of having a look at this question with a research student. It’s not clear what the right way to proceed is here — do we just have a sort of mad race where we all try to be the first to pick any low-hanging fruit that there might be, or do we have a big and multifaceted Polymath project, or do we do something in between, such as a private blog for a few people who are interested? Somewhere I saw that Gil was suggesting the Polymath approach, but I remember Nets saying after his and Michael Bateman’s previous breakthrough on the cap-set problem that he rather approved of races. The motivation for a Polymath approach might be a bit similar to the motivation for the project on prime gaps: that it will stop there being lots of small incremental papers by lots of different people. I don’t have hugely strong views on this (and in particular don’t want to pressurize others to go down the Polymath route if they don’t want to), but would be interested to know what people thought.
Dear Nets, It looks that your thoughts and especially the lovely in-between addition are way ahead of my more naive thoughts. If you can do something with anything more sophisticated than the ordinary
addition towards the integral one this would be great. Sorry I cannot say more.
Pingback: The new bound on cap sets | Anurag's Math Blog
Pingback: Ellenberg’s announcement of a solution to the cap-set problem | in theory
In reply to Tim Gowers’ frank question: I asked about corner-free sets because I personally wanted to understand the underlying idea a bit better, and hoped that someone who had started thinking about this when the Croot-Lev-Pach paper came out, rather than one day ago, might already know the answer. As for me, I do not plan to participate in either a “race” or in a “Polymath”. To me, there is little difference between the two. I participated in Polymath1 at start, and my experience was that of a race — each morning I woke up trying to digest what you, Terry and others have thought up. I would go away to think about something, and come back often only to find that whatever I thought up has been posted by someone who was faster or luckier. I did not like the experience, and have generally gravitated towards “calmer waters” in my work since.
I agree that highly active polymath projects are also races. Still, the original question makes sense, just the word “race” should be replaced by something else.
Boris: about your result. This shows that we can’t use just the fact P(x+2y) P(y+2x) =0. Thanks. But does it rule out that we could use deeper relations between P(x+2y) and P(y+2x)? Or can you get your counterexample matrix to actually be P(x+2y) and P(y+2x) for the same P.
Dear all, Since the cap set news have remarkable applications also on the sunflower conjecture that (the already running) Polymath10 is trying to study, I thought it is useful to mention this fact and think about the implication to polymath10 a little. I will be happy to see here discussion about the new breakthrough (both in connection to sunflowers or to Roth’s estimates or to other things) but let’s *not* regard this discussion as part of a polymath project but just as ordinary scientific blog discussion which can be useful for people (it can perhaps be useful to express an idea in writing and publicly even to the person who make the comment). Also I will be happy to hear news about development connected to this breakthrough.
As for polymath10, on the one hand the kind of approach I tried to promote seems now less promising than trying to push further the cap-set polynomial proof, on the other hand the Erdos-Rado conjecture itself looks more plausible now and thus the older approach while perhaps inferior is still more promising than it was before the news. In any case, I will try to proceed with it and devote to it another post.
(By the way, even now, I would regard a Fourier-theoretic proof a la Bateman-Katz for cap-set upper bounds 3^n/n^C for every C or even “just” for C=2, say, as extremely interesting although we now know much better bounds.)
Dear Professor,
A major complexity class is NL. NL is the class of languages that are decidable on a nondeterministic logspace machine. A logspace machine is a Turing machine with a read-only input tape, a write-only output tape, and a read/write work tapes. The work tapes may contain at most O(log n) symbols. In addition, Sanjeev Arora described in his book “Computational complexity: A modern approach” the certificate-based definition for NL.
The certificate-based definition of NL assumes that a deterministic logspace machine verifies the elements in a NL language using another separated read-only tape for the certificate. On each step of the machine the machine’s head on that tape can either stay in place or move to the right. In particular, it cannot reread any bit to the left of where the head currently is. For that reason this kind of special tape is called “read once”.
CLIQUE is a well-known NP-complete problem. We show that a certificate u which represents a clique V’ of size k on a graph G can be verified by a deterministic logspace machine M using an additional special read-once input tape, and thereby CLIQUE will be in NL as a direct consequence of this previous definition. If any single NP-complete problem can be solved in polynomial time, then every NP problem has a polynomial time algorithm. However, every problem in NL is in P too. Consequently, we can conclude that P = NP.
You can understand more this idea and debug my verifier algorithm in
https://hal.archives-ouvertes.fr/hal-01316353/document
Any suggestion will be welcome,
Thanks in advance,
Frank.
On 1. While Erdos-Szemeredi conjecture => Erdos-Rado (ER) sunflower conjecture is not hard to understand, how would one use a polynomial argument like this for the ER sunflower conjecture? The bound in ER sunflower conjecture is independent of n. The new technique is based on counting monomials with certain restrictions. This count would have to be independent of n for sufficiently large n and only depend on k.
On 2. As you will know, this proof by Naslund and Sawin you can find in the comments on Terence Tao’s blog.
On 4. What exactly is the conjecture for larger r? The original paper just states the conjecture for r=3. I would guess that the desired bound is
for some 
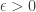for all 
? I went through Naslund and Sawin’s note and everything works fine for larger r I think. The only problem is that the bound gets worse than the trivial bound of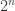 
. For example for 
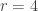I get something like 
with the argument.
Dear Ferdinand, I’ll see your comment from Terry Tao’s blog and raise you with this comment from Terry Tao’s blog by Eric Naslund. https://terrytao.wordpress.com/2016/05/18/a-symmetric-formulation-of-the-croot-lev-pach-ellenberg-gijswijt-capset-bound/#comment-468786 related to 1.
Not like I would object to it, but it is quite amusing that the above comments are just links to another blog’s comments that are just links. I wonder if there is another blog whose comments link to the above comments…
Oh, I am similiarly amused. But all these references are clearly relevant for the mentioned questions.
Thanks for pointing out the second comment by Eric Naslund. That is very nice. I think. If I read it correctly, this is a direct proof (at least a case of) of Conjecture 4 of Alon-Shpilka-Umans, which is equivalent to the Erdos and Szemeredi conjecture. So it is still a version of the the sunflower conjecture that allows the bound to grow with the size of some universe. In that sense I still have no idea how to obtain a polynomial bound that does not depend on the size of “some universe”.
I think that the new paper by Eric push the state of knowledge from Erdos-Szemeredi sunflower conjecture toward the Erdos-Rado direction. Let me mention that a major challenge for Erdos Rado is proving a
upper bound. (Or even smaller improvement on Kostochka’s bound.)
What kind of bound on $$C_D$$ in the Eric Naslund paper would we need in order to prove a $$(k!)^{1-\epsilon)$$-bound for the weak sunflower conjecture?
⭐ 😎 ❗ 💡 impressive/ amazing recent advances esp the short proof by ellenberg 🙂
sunflowers show up in razborovs proof of the “monotone P vs NP” and in some other analysis eg Rossman. my question, could there be a conjecture on sunflowers or something similar that is equivalent to the P vs NP problem (or maybe P/poly vs NP)?
As Ryan Williams pointed out to me, the bounds on the dimension can be improved somewhat using techniques from my paper http://theoryofcomputing.org/articles/v007a013/v007a013.pdf . Let me focus on the multi-linear case for simplicity, but this also works in the more general setting.
Let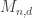
denote the set of degree 
monomials in 
variables, where in the multi-linear setting 
. The current works showed (implicitly) that there exist 
subsets ![A_i, B_i \subset [n]](https://s0.wp.com/latex.php?latex=A_i%2C+B_i+%5Csubset+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002)
such that any subset ![S \subset [n]](https://s0.wp.com/latex.php?latex=S+%5Csubset+%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002)
of size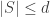 
is contained in 
for some 
. This was done by choosing for 
all possible subsets of ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D&bg=ffffff&fg=333333&s=0&c=20201002)
of size 
. This then implied a bound of 
on the rank of an appropriate matrix (or tensor, as given in the symmetric version in Terry’s blog).
However, the bound on
can be improved to 
by a more careful choice. The idea is simple: let 
enumerate the intervals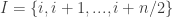 
for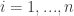 
, where values are taken modulo 
. For each such interval 
, take for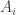 
all subsets of 
of size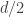 
of it, and for 
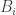all subsets of the complement of 
of size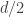 
.
In general, it seems that this allows one to take $approx N \approx \sqrt{|M_{n,d}|}$ even in more general settings, which would improve the bounds for cap sets and the weak sunflower theorem.
Are you saying that bounds on cap sets might be improved from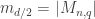
to the square root of that? Wouldn’t that break the known lower bounds on cap sets? For the case of 
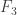we have an upper bound of 
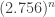, while the lower bound is something like 
. May be you meant something else?
correction:
instead of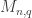 
and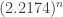 
instead of 
Actually, I am not sure if it works. What I wrote works for a polynomial
in one set of 
variables, but once you decompose 
and need the decomposition to the 
and 
components, it is less clear to me that what I wrote works.
Dear all, many thanks for all the remarks. I was participating in a conference and did not have time to think and even just to respond to the many interesting comments. Looking back at my old cap set posts from 2009 I came to the following question: Let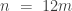
(and you may assume 
is a prime if its help or even change the parameters differently) consider a subset 
of 
without three vectors x, y and z such that there are precisely 
coordinates for which 
for every vector $\latex (a,b,c)$ with either 
or 
. (12 vectors altogether.) Is it true that 
for some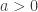 
? Perhaps the CLPEG-polymomial argument can give this as well.
We need here to consider only balanced vectors (with the same number of 0,1,2).
(Maybe we can consider more general vectors and modify the condition.to demand that we do not have three vectors that the distribution of triples of coordinates is given precisely by the product of individual distributions. )
A nice and not overly strong version of the conjecture is this. Let
be a subset of 
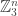without three distinct vectors 
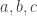that sum-up to zero, and the number of coordinates where 
is the same as the number of coordinates where 
. (Everything is modulo 3, of course.)
(In other words, in a 3-term AP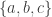
in 
there are three kind of coordinates: those where the three vectors agree, those where they are of the form
for some 
and those where they are of the form 
for sum 
. We want to exclude only 3-terms AP only of the kind where there is equality between coordinates of the two later kinds. This does not depend on the ordering of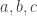 
and it is preserved when you add the same vector to all three.)
Conjecture:
is exponentially smaller than 
. (Namely, 
for some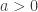 
.)
I am curious if the CLPEG-argument can be adapted. (perhaps under some additional arithmetic conditions on
). (If we try to adopt Tao’s symmetric proof we need to show that some more complicated function associated to this question is of “low rank”.)
Pingback: Polymath 10 post 6: The Erdos-Rado sunflower conjecture, and the Turan (4,3) problem: homological approaches. | Combinatorics and more
Pingback: 月旦 IV | Fight with Infinity
Pingback: A Simple Proof From the Pattern-Matching Card Game Set Stuns Mathematicians | News Today
Pingback: A Simple Proof From the Pattern-Matching Card Game Set Stuns Mathematicians | News
Pingback: Polynomial Prestidigitation | Gödel's Lost Letter and P=NP
Pingback: Polymath10 conclusion | Combinatorics and more
Pingback: co.combinatorics - Is there any relationship between Szemerédi's theorem and Sunflower conjecture? Answer - Lord Web