Thomas Bloom and Olof Sisask: Breaking the logarithmic barrier in Roth’s theorem on arithmetic progressions, arXiv:200703528
Once again Extraordinary news regarding Roth Theorem! (I thank Ryan Alweiss for telling me about it and Rahul Santhanam for telling me about Thomas and Olof’s earlier attempts.)
Suppose that 
A few days ago Thomas Bloom and Olof Sisask proved that for some
This is an extraordinary result!!! I will tell you a little more about it below.
Ron Graham
I just heard yesterday the sad news that Ron Graham passed away. Ron was an extraordinary mathematician and an extraordinary person. I first met Ron in Montreal in 1978 and we met many times since then. Ron will be dearly missed.
Back to the new bounds on Roth’s theorem
From an abstract of a lecture by Thomas and Olof: “This is the integer analogue of a result of Bateman and Katz for the model setting of vector spaces over a finite field, and the proof follows a similar structure.”
A catchy (weaker) formulation which goes back to Erdos and Turan is:
Let 
Bloom and Sisask’s result implies, of course, Van der Korput’s result that the primes contain infinitely many 3-terms arithmetic progression as well as Green’s 2005 result asserting it for every dense subset of primes.
Szemeredi’s celabrated result extended Roth’s theorem to arithmetic progression of any fixed size, and Green-Tao celebrated 2008 result asserts that the primes (or a dense subsets of primes) contain arithmetic progression of any length. (The case of 3-term AP is so far much simpler for all the results mentioned below.)
A little more about the history of the problem below the fold
Roth, Szemeredi, Heath-Brown, and Bourgain; Salem-Spencer and Behrend.
Let’s wrire 
$latex c>0$ (Szemeredi’s argument gave
Erdös and Turan who posed the problem in 1936 described a set not containing an arithmetic progression of size 
Sanders
In 2010 Tom Sanders was able to refine Bourgain’s argument and proved that 
We reported about this outstanding achievement in this blog post and quoted from his paper: “There are two main new ingredients in the present work: the first is a way of transforming sumsets introduced by Nets Katz and Paul Koester in 2008, and the second is a result on the 
The exponent 6 for the loglog term was improved to 4 by Thomas Bloom and recently to 3 by Thomas Schoen in his paper: Improved bound in Roth’s theorem on arithmetic progressions. Schoen uses ingredients from Bateman and Katz’s work (see below).
Cap sets – Meshulam
A closely related problem in 
Bateman and Katz
In 2011, Michael Bateman and Nets Katz improved, after many years of attempts by many, the Roth-Meshulam bound. They proved using Fourier methods that 
Polymath 6
Tim Gowers proposed in 2011 polymath6 to try to break the logarithmic barrier for Roth based on the Bateman-Katz breakthrough. (Here is the wiki; and a related post by Sanders, and a document by Katz) This project did not get off the ground. We can regard the news as giving support that the polymath6 project was timely and of an appropriate level, and also as giving some support to an advantage of the conventional way of doing mathematics compared to the polymath way.
Croot-Lev-Pach-Ellenberg-Gijswijt solution to the Cap set problem via the polynomial method
Next and quite recently came a startling development – the Croot-Lev-Pach-Ellenberg-Gijswijt capset bound 
A natural question that many people asked was how this development relates to improving the bounds for Roth perhaps even towards the Behrend bound. We discussed it a little over here and in other places. This is still an interesting possibility.
The new result: Bloom and Sisask
However, just a few months few years after the Bateman-Katz result have become obsolete for the cap-set problem, the Bateman-Katz method prevailed in this wonderful breakthrough of Bloom and Sisask giving 
Congratulations!!!
An old post and poll
In an old post we asked: “How does 
Combinatorics and more 
Very nice summary of the history of the problem!
Pingback: Silver linings | in theory
It is irresponsible to endorse a result as correct without having first checked the proof.
This is a good point! My policy here over the blog is to write about preprints (and sometimes about results announced in lectures) where I see a good chance that the result will prevail. Of course, there were a few cases that I endorsed results where a gap was later found or where they are still pending after several years.
There are some subtle historical issues regarding the conjecture that subsets of the integers which are as dense as the primes (or for which the sum of reciprocals diverges) contains sufficiently large AP. This is discussed in the paper “New applications of the polynomial method: The cap set conjecture and beyond” by Joshua A. Grochow (footnote 1 p. 33). What Josh writes is: “Regarding the date of this conjecture, the earliest written reference I could find for the case of 3-term arithmetic progressions was a 1973 seminar report, and for general arithmetic progressions was a talk from 1976. This conjecture is often attributed to Erdos and Turan’s 1936 paper, but the conjecture does not appear there in print—even as a question— and in his later writings, including a touching tribute to Turan, although Erd˝os raises the problem in connection with his work on the primes with Turan, he refers to it as an “old conjecture of mine” (emphasis added).” The Erdos Turan paper mentioned that a conjecture at the time by Szekeres on the density that force k-term AP would imply sufficiently long AP of primes.
It is also an interesting question regarding the origin of the conjecture that the primes contain sufficiently large AP. The Green-Tao paper asserts “It is a well-known conjecture that there are arbitrarily long arithmetic progressions of prime numbers. The conjecture is best described as “classical”, or maybe even “folklore”. In Dickson’s History it is stated that around 1770 Lagrange and Waring investigated how large the common difference of an arithmetic progression of L primes must be, and it is hard to imagine that they did not at least wonder whether their results were sharp for all L.”
I’m recalling that Chowla may have discussed primes forming k-APs for k greater than 3, not just k=3 back in the 1930s.Probably in an LMS publication.
I am not surprised that the Erdos-Turan k=3 case is true.
I am utterly shocked that it was proven!
I thought it was one of those hopeless problems, and the results closing in on it seemed to
be almost an admission of how hard it is: we can’t get n/(log n)^{>1} but we can get
n(log log n)^4/log n.
So here is my question: Gil, and anyone else who wants to comment- are you surprised that
it was proven (in the year 2020)?
Dear Bill, thanks for the comment. This is an amazing breakthrough but I did not regard it a hopeless beyond hopeless task especially that I knew that Bloom and Sisask (and perhaps others) were working on it and were hopeful.
Are you, or they, hopeful for k=4? For the general case of k?
I cannot answer for them and their view is certainly more meaningful than mine, but to me k=4 looks like a very far away goal.
I don’t think the fact that it was proven for k=3 was a big surprise to those in the area – once the breakthrough paper of Bateman and Katz appeared in 2010, it was clear that there were some ideas capable of breaking through the logarithmic barrier. It was difficult getting those ideas to work in the integers (which needed some other ideas besides), but not impossible.
I personally think that the case k=4 is attainable, probably within the next 10 years, if a sufficient amount of time and energy was spent on it. The advantage of k=4 is that it is only a ‘little bit’ more complicated than k=3 (in that, for example, the gulf in difficulty between k=4 and k=5 is vastly wider than that between k=4 and k=3). In particular, thanks to recent work of Green and Tao, we do have at least a polylogarithmic bound for k=4, which is much better than k=5.
It is possible that most of the ideas to prove what is required in the k=4 case are already present, between the paper of myself and Olof, and the work of Green and Tao, and perhaps some of the ideas in the revolutionary quantitative advances made in understanding the higher Gowers uniformity norms by Manners.
But actually working out how to get all of this working together seems a very difficult task, and would take a lot of time and energy I think. (I certainly am taking a break to think about other, non-AP, problems!) But I would not be very surprised (but would be very impressed) by a proof of the k=4 case.
The k=5 case, on the other hand, I am much more sceptical about the chances of anything working for in the next few years. Indeed, I am not entirely convinced that the conjecture should even be true for k=5 and higher…
Many thanks for the comment, Thomas. Indeed the big additional gap between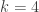
and latex k>4$ is of great interest and although I heard about it I don’t understand it.
Thanks, Thomas, very interesting! Is there somewhere someone – perhaps you? – has written about why the gap between 4 and 5 is thought to be so difficult, or could you say a few more words here? I’m very curious. (In the F_3^n case, there’s also a pretty significant gap between 3 and 4 – just as one example, the Croot-Lev-Pach/slice rank method doesn’t seem to give any nontrivial bound in the k=4 case. I think Tao has a blog post about it.)
I think I would be very surprised if the case $k = 4$ were handled any time soon, either by itself or as part of a general proof for $k \geq 4$. The argument of Terry and me which gives $r_4(N) \ll N (\log N)^{-c}$ gives a very small constant c for a variety of different reasons, if I recall correctly, and the same is true for the finite field model of the problem (our paper gives $c = 2^{-22}$ or something in that case). Moreover, even in the finite field variant of the problem, the exponent 1 is not in any way a “natural barrier” in the problem in the same way that it was for $k = 3$. So instead of needing to go an epsilon beyond some natural barrier, where you can try and very carefully examine what kind of thing would have to happen for near-equality to occur in the best known argument (this being essentially the nature of the Bateman-Katz argument, and your argument with Olof) I don’t see any reason why proving $r_4(N) \ll N(\log N)^{-1 – \delta}$ should be any easier than proving $r_4(N) \ll N(\log N)^{-2}$, which of course implies $r_3(N) \ll N(\log N)^{-2}$, about which we currently have few ideas.
Good points Ben! I’ll modify my previous comment by adding the caveats that
1) the k=4 case would be very difficult (an order of magnitude at least more difficult than the k=3 case, for example),
2) I’d expect before the log barrier was passed for k=4 a much better bound (e.g. of Behrend-type) for k=3 would be proved.
That is, I don’t think that the current bound of ‘just past log’ for k=3 would next be proved for k=4, I think the technology for k=3 would first be much improved/streamlined to the point where it was a lot more obvious how to use them to get a small win for k=4.
You raise the excellent point that probably, before getting past log for k=4, likely precusor results would be 1) obtaining a density bound like 1/(log N)^c for some reasonable constant c (like 1/2 or even 1/4) for k=4 in the integers, and 2) getting past 1/log N in a model setting like F_5^n.
So yes, I would be surprised if the log barrier for k=4 was broken past before these things happened!
What is special about 3-APs in this? View 3-APs as sol to x-2y+z=0
What about x+y+z=0 when taking the interval to be [-N,N].
Does an easy tweek of the proofs or even just of the problem get
a) Sz theorem for x+y+z=0
b) Erdos-Turan for x+y+z=0, using \sum 1/|a|
Apologies if these are either obvious or well known open problems, but never a good idea
to self-censor.
bill g.
I think this is a very good question and some aspects of the theory extends to various cases of equations where there are at least two more variables than equations.
There is nothing special about 3APs – the proof would apply equally well to any translation invariant linear equation (that is, an equation of the form c_1x_1+…+c_kx_k=0 where c_1+…+c_k=0).
A couple of important remarks, however:
1) Translation invariance is absolutely crucial here, and this is not just an artefact of the proof, since without translation invariance it is easy to come up with positive density sets without solutions, using congruence restrictions. For example, with your example x+y+z=0 we could just take all the odd numbers in [-N,N], giving a set without solutions of density 1/2.
2) When we have at least 4 variables, much better bounds are available (see https://arxiv.org/abs/1408.2568 by Schoen and Sisask). So our new result is only really relevant when we have exactly 3 variables.
In general, I’d expect the method to also work whenever we have a system of r translation invariant linear equations in at least 2r+1 variables. Roth himself showed how his original method works for such a system, and I’d expect the method to generalise straightforwardly, the main issue being the inevitable notational complexity. But I haven’t checked this myself.
(I am sure I am confused here).
4AP can be expressed as w – x – y + z = 0, so the coeffs all add to 0, so reading your first paragraph it seems like you have cracked the 4AP problem OR (much more likely) I am confused.
That is not a 4ap, just an ‘additive tuple’. For example, 1, 7, 2, 6 satisfy the equation a+b=c+d.
What is true is that this equation plus the equation for a 3ap defines a 4ap, so a 4ap is defined by the pair of equations a+b=2c and a+c=b+d. This is a system of translation invariant linear equations, but sadly in 4 variables with 2 equations, just shy of the threshold for Roth based techniques to work.
Pingback: Péter Pál Pach and Richárd Palincza: a Glimpse Beyond the Horizon | Combinatorics and more
Pingback: To cheer you up in difficult times 20: Ben Green presents super-polynomial lower bounds for off-diagonal van der Waerden numbers W(3,k) | Combinatorics and more
Pingback: Barnabás Janzer: Rotation inside convex Kakeya sets | Combinatorics and more
Pingback: Greatest Hits 2015-2022, Part II | Combinatorics and more
Pingback: Absolutely Sensational Morning News – Zander Kelley and Raghua Meka proved Behrend-type bounds for 3APs | Combinatorics and more