Touching Simplices and Polytopes: Perles’ argument

Posted on August 27, 2017 by Gil Kalai

Joseph Zaks (1984), picture taken by Ludwig Danzer (OberWolfach photo collection)

 

The story I am going to tell here was told in several places, but it might be new to some readers and I will mention my own angle, recall and raise some questions  and provide some comments. You can read about it here: Martin Aigner and Günter Ziegler, Proofs from the Book Chapter 13 (freely available on Springer links), and also in Bela Bollobas, The Art of Mathematics – Coffee Time in Memphis.

Can you find  non-overlapping d-dimensional polytopes P_1,P_2,\dots ,P_k be, in \mathbb R^d, such that each pair of polytopes have (d-1)-dimensional intersection, and such that  P_i has f_i facets? In two dimensions k \le 4 (because K_5 is not planar) but in higher dimensions things are not clear. We call two d-polytopes in \mathbb R^d “touching” if they have (d-1)-dimensional intersection (no more, no less).

A special case of this problem deals with the case that all the P_is are simplices (thus having d+1 facets each) and then the question is how large k can be? The problem goes back to a 1956 paper by Bagemihl. A famous conjecture  by Bagemihl (space) and Baston (all dimensions) asserts that k \le 2^d. Joseph Zaks gave a beautiful example of 2^d simplices in \mathbb R^d with this property. Baston proved that in space k \le 9 and, based on his work and a great deal of extra effort, Joseph Zaks verified Bagemihl’s original conjecture! He thus proved that in space k \le 8. The conjecture in higher dimensions is wide open.

Let me show you a very simple proof by Micha A. Perles that k \le 2^{d+1}.

Let n be the overall number of hyperplanes supporting the facets of the polytopes and let H_1,H_2, \dots , H_n be these supporting hyperplanes. For each hyperplane H_i we denote the two closed half spaces determined by it by H_i^+ and H_i^-. Now let us suppose that in our family of polytopes there are r_j polytopes with j facets, j=d+1,d+2,\dots.

Theorem:

 

(*) \sum r_j 2^{-j} \le 1.

In particular, if all polytopes are simplices we get that k\le 2^{d+1}.

Proof (Micha A. Perles):  Consider a matrix M=(m_{ij}) whose rows correspond to the k polytopes and whose columns correspond to the n hyperplanes.

The entries are:

m_{ij}=1 if H_j contains a facet of polytope P_i, and P_i \subset H_i^+.

m_{ij}=-1 if H_j contains a facet of polytope P_i, and P_i \subset H_i^-.

Otherwise, m_{ij}=0.

Now replace each row of the matrix by new 2^{n-f_i} rows by replacing every zero entry by a \pm 1 entry in all possible ways.  (Recall that polytope P_i had f_i facets.)

Claim: All the new rows are distinct.

Proof: This is clear for two new rows coming from the same original row. Given two rows which correspond to distinct polytopes P_e and P_f, since these polytopes are touching, in the original rows there is a column j for which m_{ej}=1 and m_{fj}=-1 or the other way around. These pair of distinct entries remain unchanged when zeroes are replaced by \pm 1. Ahla!

Returning to the theorem, since there are altogether 2^n vectors of \pm 1 entries we get that

\sum _{i=1}^k 2^{n-f_i} = \sum_{j \ge d+1} r_j 2^{n-j} \le 2^n. Dividing by 2^n gives us the theorem.  Sababa!

 

Of course, we can ask if a stronger inequality is valid and propose that

Conjecture  (**): \sum r_j 2^{-j} \le 1/2.

Another question is when (for d \ge 3) can we realize “r-vectors” obeying the strong inequality (**) by a family of touching polytopes.

Twelve quick remarks:

  1. Perles’ argument is close in spirit to a proof technique in extremal combinatorics that we saw, for example, in the proof of Sperner’s theorem on antichains and in the proof of the “two family theorems“. (Here and below you can find links to earlier blog posts, but not to the precise location in those posts.)
  2. Inequality (*) resembles the LYM inequality.
  3. Zaks’ example of 2^d touching simplices in \mathbb R^d is beautiful. See his paper Neighborly family of 2^d simplices in E^d. (Or here.)
  4. Let us call a facet of a polytope in the family “free” if it does not touch any other polytope. Zaks made the following conjecture: In every family of touching d-simplices (d-polytopes) in \mathbb R^d, there is a free facet (to at least one of the polytopes.)
  5. In a family of touching simplices if every simplex has a free face then k\le 2^d. (More generally, for touching polytopes with this property (**) holds.)
  6.  It would be very nice to prove the 2^d upper bounds for families of touching simplices (and inequality (**) for families of touching polytopes) such that in the family and in every subfamily at least one simplex has a free facet.
  7. Related to comments 1 and 6. Is there an algebraic/topological proof of the known inequality which will enable to use Zaks’ free-facet conjecture? Possible role model: Lovasz’ algebraic proof (and geometric extension) of the two-family theorem.
  8. Two d-polytopes P,Q in \mathbb R^d are weakly touching if there is a hyperplane containing a facet of both that (weakly) separates them.
  9. Perles’ proof and inequality (*) extend for families of weakly touching polytopes. It may be the case that the conjectures of Bagemihl and Baston and inequality (**) extends for weakly touching polytopes.
  10. Zaks’ free-facet conjecture does not extend for weakly touching simplices.
  11. In my first meeting with Gunter Ziegler in 1984 we talked about this problem. (We had both worked on it previously).
  12. We use here again the convention of ending proofs with the words Walla and Sababa. The endings Ahla, Ashkara (for trivial proofs), and Fadiha (for wrong proofs) can also be used.

A   fantasy for attacking the problem based on points 4,6,7 above is given in the following figure

Coxeter’s MathSciNet review of Baston’s Book

Baston, V. J. D. , Some properties of polyhedra in Euclidean space.
International Series of Monographs in Pure and Applied Mathematics, Vol. 71 Pergamon Press, Oxford-Edinburgh-New York 1965 xi+209 pp.

F. Bagemihl [Amer. Math. Monthly 63 (1956), 328–329; MR0077132] considered a set of n tetrahedra (in three-dimensional space) which fit together without overlapping so that every two of them have a common boundary (part of a face) of positive area. After proving that n can be 8, and that n≤17, he conjectured that 8 is the greatest possible value of n. The author, in the first chapter, reaches the same conclusions independently, representing the arrangement by a matrix of n rows whose entries are all 1, 0 or -1. In the remaining nine chapters he reduces the upper bound from 17 to 9, still leaving for future research the possibility of an arrangement with n=9.

The presentation is enlivened by colorful nomenclature; for instance, one reads, on page 181, “As S3 contains five dotres and no treuns there are ten tripts in the matrix. As there are four naiks…” Although such passages are less poetic then “All mimsy were the borogoves, and the mome raths outgrabe”, there is again the comforting thought that each unfamiliar word is precisely defined in another part of the book. Moreover, the index reassures us that there are only 24 such words, including Lewis Carroll’s old friend, the dodo.

Reviewed by H. S. M. Coxeter

 

This entry was posted in Combinatorics, Convex polytopes, Geometry, Open problems and tagged , . Bookmark the permalink.

3 Responses to Touching Simplices and Polytopes: Perles’ argument

  1. Pingback: Greatest Hits 2015-2022, Part I | Combinatorics and more

  2. dsp says:
    July 19, 2023 at 6:20 pm

    I think I have an approach to establishing the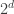 2^d upper bound that follows your program of trying to find an algebraic proof modeled on Lovasz’ proof of the two-families theorem. It goes exactly like that proof, except with the exterior algebra replaced with the geometric (Clifford) algebra:

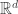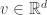    Recall that the real geometric algebra \mathcal{G}(\mathbb{R}^d,q) with respect to a quadratic form q on \mathbb{R}^d is the tensor algebra on <\mathbb{R}^d modulo the relations v \otimes v = q(v,v) for all vectors v \in \mathbb{R}^d. In particular, if we take the standard inner product whose matrix is the identity matrix as the quadratic form, and a unit vector u, then (1-u)(1+u) = 1 - u + u - uu = 1 - u + u - 1 = 0 in that geometric algebra.

    Now for each simplex \sigma in our collection whose facets have outer unit normal vectors u_{\sigma,1},\dots,u_{\sigma,d+1}, take the element e_{\sigma} := (1+u_{\sigma,1}) \cdots (1+u_{\sigma,d+1}) of the geometric algebra. Now I can prove that whenever \sigma_1, \sigma_2 are two touching simplices, then e_{\sigma_1}e_{\sigma_2} = 0. 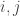Note that this would be immediate if the geometric algebra were commutative, since we would then have u_{\sigma_1,i} = -u_{\sigma_2,j} for some i,j, and therefore (1+u_{\sigma_1,i})(1+u_{\sigma_2,j}) = 0 by the identity we noted in the previous paragraph. Of course, the geometric algebra is not commutative, but I think I have found a way to work around that using traces (a bit like the Razmyslov transform in polynomial identity theory).

    Suppose we could now prove that both (1) e_{\sigma} \neq 0 and (2) e_{\sigma}^2 \neq 0 for every simplex \sigma. 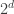Then we would have exactly the situation of Lovasz' proof of the two-families theorem for the collection of touching simplices \{\sigma_i\}_i in the sense that e_{\sigma_i}e_{\sigma_j} \neq 0 iff \sigma_i = \sigma_j, and therefore the e_{\sigma_i} would be linearly independent elements of the geometric algebra, and since that algebra has dimension 2^d, we would be done.

    What do you think? (For more on geometric algebras, see this wonderful survey).

    Reply

Leave a comment