Frankl’s Conjecture for Large Families: Ilan Karpas’ Proof

Posted on March 9, 2018 by Gil Kalai

Frankl’s conjecture asserts that a for every finite family of of finite sets that is closed under union, there is an element that belongs to at least half the sets in the family. We mentioned the problem in our very first post, and Tim Gowers ran polymath 11 in attempt to solve it (first post, wikipage). See also this post over GLL and this post.

Here, I want to show Ilan Karpas’ proof (that we mentioned in this post) that the conjecture is correct for “large” families, namely, for families of at least 2^{n-1} subsets of [n]. Karpas’ proof is taken from his paper  Two results on union closed families.

Can Fourier methods solve Frankl’s conjecture? I hope we could have a small discussion about it and related matters, and, in any case, I myself have some comments that I will leave to the comment section.

The theorem

Theorem (Karpas): If B is a union closed family of subsets of [n], and |B| \ge 2^{n-1} then there exists an element k \in [n] such that |\{S \in B: k \in S\}| \ge |B|/2.

Theorem 2 (Karpas): If A is a family of subsets of [n], |A|\le 2^{n-1} with the property

(*) If S\in A and a,b \in S, a\ne b then either S \backslash \{a\}\in A or S \backslash \{b\}\in A.

Then there exists an element k \in [n] such that |\{S \in A: k \in S\}| \le |A|/2.

The implication from Theorem 2 to Theorem 1 is very easy. If B is a union-closed family and A is the complement of B, then B satisfies (*). (Otherwise,  S \backslash \{a\}\in B and S \backslash \{b\}\in B and their union S must be in B. If B has at least 2^{n-1} elements then A has at most 2^{n-1} elements. If |\{S \in A: k \in S\}| \le |A|/2, then |\{S \in B: k \in S\}| \ge |B|/2. We note that Condition (*) is weaker than the assertion that A is union closed and indeed the assertion of Theorem 2 is sharp do not hold when |A| is large. (See remark below.)

Background (a little more than needed)

Edge boundary/influence terminology

For a family A of subsets of [n] its edge-boundary is defined by E(A,\bar A)= \{(S,T)  d(S,T)=1, S \in A, T \notin A\}

The total influence of A is defined by I(A) = \frac {1}{2^{n-1}}|E(A,\bar A)|

Up and down edge boundaries:

E^-(A,\bar A)= \{(S,T) : d(S,T)=1, S \in A, T \notin A, T \subset S \}

E^+(A,\bar A)= \{(S,T) : d(S,T)=1, S \in A, T \notin A, S \subset T \}

I^+(A) =2^{-(n-1)}|E^+(A,\bar A)|

I^-(A) =2^{-(n-1})|E^-(A,\bar A)|

Directional boundaries and individual influences

We now define:

I_k^-(A)= 2^{-(n-1)}|\{S \in A, k \in S, S \backslash\{k\} \notin A \}|,

I_k^+(A)=2^{-(n-1)}|\{S \in A, k \notin S, S \cup \{k\} \notin A \}|,

The influence of k on A is defined by:

I_k(A)=I_k^+(A)+I_k^-(A)

Note that the assertion for Frankl’s conjecture is equivalent to: For every union-closed family B there is k such that I_k^-(B) \ge I_k^+(B). Equivalently for every family A whose complement is union-closed (such families are called “simply rooted”) there is k such that I_k^+(A) \le I_k^-(A).

Sensitivity/Pivotality

Now, fix a family A of subsets of [n], for S \in A, h_k(S) = 1, if S \delta \{k\}\not in A and h_k(S) = 0 otherwise. h^+_k(S)=1 if k \in S and h_k(S) = 1. (In other words, k \in S and S \backslash \{k\}\notin A.) h^-_k(S)=1 if k \notin S and h_k(S) = 1. (In other words, k \notin S, and S \cup \{k\}\notin A.) Define also h(S) = h_1(S)+h_2(S)+\cdots h_n(S), h^+(S) = h^+_1(S)+h^+_2(S)+\cdots + h^+_n(S), h^-(S) = h^-_1(S)+h^-_2(S)+\cdots + h^-_n(S).

Note that I_k^+(A)=2^{-(n-1)}\sum_{S \in A} h_k^+(S), and similarly for other types of influences.

Fourier

Let f:\{0,1\}^n \to \{-1,1\} be a Boolean function defined as follows: f(x)=-1 if x represents a set in A, and f(x)=1, otherwise.

We write \hat A(S)=\hat f(S).

It is well known and easy to see that \hat A(\{k\})=I^+_k(A)-I^-_k(A).

Parseval’s formula gives \sum \hat A^2(S)=1. It follows easily from Parseval’s formula that I_k(A)=\sum \{\hat A^2(S):k \in S\},  and hence I(A)=\sum \hat A^2(S)|S|.

The proof:

We write |A|=(1/2-\delta) 2^n.

Our assumption (*) on A is that if S\in A and a,b \in S, a\ne b then either S \backslash \{a\}\in A or S \backslash \{b\}\in A. In other words h^+(S) \le 1 for every S \in A. This implies that

(1) I^+(A) \le 2^{-(n-1)}|A|=(1-2\delta ).

We assume that Frankl’s conjecture is false namely that \hat I^+_k(A) > I^-_k(A), for every k, or equivalently that

(2)  I_k^+(A)- I^-_k(A) = \hat A(\{k\}) > 0, k=1,2,\dots ,n.

Summing over all ks it follows that I^-(A) < I^+(A) hence

(3) I(A)  < 2I^+(A) \le 2-4\delta.

From I(A)=\sum \hat A^2(S)|S|, it follows that

(4)  I(A) \ge 2 - \sum\hat A^2(\{k\}) - 2\hat A^2 (\emptyset ).

Note that

(5) \hat A^2(\emptyset )=4\delta^2

But

(6) \sum \hat A^2(\{k\}) \le \sum \hat A (\{k\}) = I^+(A)-I^-(A)

Combining (4,5,6)  we get

I^+(A)+I^-(A) \ge 2 - I^+(A)-I^-(A) - 4(\delta^2), or

(7) 2I^+(A) \ge 2-8\delta^2.

(1) and (7) gives 1-2\delta >1-4\delta^2, a contradiction.

 

This entry was posted in Combinatorics, Mathematics over the Internet, Open problems and tagged , , , . Bookmark the permalink.

13 Responses to Frankl’s Conjecture for Large Families: Ilan Karpas’ Proof

  1. Ilanka . says:
    March 9, 2018 at 1:25 am

    Thanks!

    Very clear explanation.

    Best,

    Ilan

    On Thu, Mar 8, 2018 at 11:33 PM, Combinatorics and more wrote:

    > Gil Kalai posted: “Frankl’s conjecture asserts that a for every finite > family of of finite sets that is closed under union, there is an element > that belongs to at least half the sets in the family. We mentioned the > problem in our very first post, and Tim Gowers ran polymath” >

    Reply
  2. Gil Kalai says:
    March 11, 2018 at 10:59 am

    Remark (1): Balla, Bòllobas and Eccles proved that for every union-closed family B of subsets of N of size at least \frac{2}{3}2^n there is a good element. In fact, they showed that in this case I^-(B) \ge I^+(B). For |B|\ge (3/4) 2^n, this follows easily from the isoperimetric inequality. If A satisfies (*) and |A| \le (1/4) 2^n. Than the Harper bound asserts that I(A) \ge 2|A| 2^{-(n-1)}. But (*) gives that I^-(A) \le |A|2^{(n-1)} and if I^+(A)<I^-(A) we get that I(A)=I^+(A) + I^-(A)<2|A|2^{(n-1)}. A contradiction.

    Reply
  3. Gil Kalai says:
    March 12, 2018 at 9:46 am

    Remark (2): Tom Eccles improved the result of Balla, Bòllobas and Eccles further and showed that the assertion of Frankl’s conjecture holds when |{\cal A}|\ge (2/3-1/104)2^n.

    Ilan Karpas proved in his paper that for some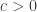 c>0, the assertion of Frankl’s conjecture holds when |{\cal A}|\ge (1-c) 2^{n-1}.

    Reply
  4. Gil Kalai says:
    March 15, 2018 at 4:15 pm

    Remark (3): Here is Ilan’s example showing that Theorem 2 does not hold for every A. To see this consider the family {{2},{3},{1,2},{1,3},{1,2,3}} of five subsets of {1,2,3}. Every element is included in more than half the sets and consition (*) is satisfied. The complement {{},{1},{23}} is not union-closed.

    Reply
  5. Roy Abrams says:
    March 15, 2018 at 8:05 pm

    Is this reasoning valid:
    1. Frankl’s Conjecture asserts that in any family of sets (1,2,3…) that is union closed, there is a least one element (a,b,c…) found in at least half of all the subsets of the set containing all elements in the family.

    2. Arrange the sets in ascending order of cardinality, from smallest set to the set containing all elements. Sets of equal cardinality can be put in any order within the overall arrangement.

    3. The smallest set is “irreducible.” The union of any two sets is either a subset of the larger one, or has cardinality greater than the larger one, or is, in the case of two sets of equal cardinality, a set of greater cardinality.

    4. Number the sets from 1 to N in ascending order, N being the set of greatest cardinality.

    5. Create the power set of all sets, 1 to N – 1.

    6. Because set union is associative and commutative, and because union-closed families include every union, every set represented in the power set is a member of the union closed family, one of the numbered sets used as generators.

    7. Some of these sets are entirely contained in their set of greatest cardinality. Some include all the sets enumerated, but belong to a set of greater cardinality that is not part of the bracketed sets.

    8. Because the number of subsets of the power set is strictly larger that the set containing the original elements (and grows exponentially), each element will be represented by multiple subsets of the power set.

    9. Therefore multiple subsets will be equivalent, representing the same unique generating set.

    10. Equivalence of these subsets of the original set implies intersections, i.e., element(s) (a,b,c…) appear in more than one generating set.

    11. Using the ‘irreducibility” of the least set (1), you should be able to establish a chain of subsets in which one is included in more than half the original sets (1,2,3…). Obviously, the power set grows must faster than the number of original sets, so a kind of induction might be possible.

    12. For example, establish that 1 is a proper subset of 3, establish that 3 is a proper subset of 6, etc.

    Reply
    • Roy Abrams says:
      March 22, 2018 at 6:04 am

      13. Perhaps it’s needless to add, that you could create something similar to Von Neumann’s ordinals, with nested sets, on which to create an algebra of equivalences.

      Reply
  6. Guabuzi says:
    March 16, 2018 at 4:14 am

    Can you give a reference to the “well-known result” \hat{A}(\{k\})=I_k^+(A) - I_k^-(A)? From your definition of I_k^+(A) and I_k^-(A) I can only derive \hat{A}(\{k\})=I_k^-(A) - I_k^+(A), the opposite of what is claimed. Besides, if assume Frankl’s conjecture is false, what I can derive is I_k^+(A)<I_k^-(A), which is also the negate of what is claimed in the paper.

    Thanks.

    Reply
  7. Roy Abrams says:
    March 16, 2018 at 11:26 pm

    To refer back to my comment above. If we create the power set of the sets of any union-closed family, and agree that each of the new sets exist, does it not imply that every set (rather than element) appears in exactly half the sets, tightly. And that therefore any elements in each set appear in at least half the sets? The fact that they appear more frequently in actual examples of union-closed families, and the reason union closed families of N sets can have less than 2 to the N power is because there are intersections between all of the sets–i.e., they share elements? In other words, the conjecture is true, and more apparent if one considers the sets and their frequency, rather than the elements?

    Reply
  8. Roy Abrams says:
    March 16, 2018 at 11:35 pm

    Correction–that should be the power set of 1 to the N-1 sets, as stated in my first comment.

    Reply
  9. Roy Abrams says:
    March 21, 2018 at 7:24 am

    Hope I’m not belaboring an errant line of thought, but obviously, every set in the power set has its complement, which would appear to preclude an element of one of the sets composing the power set appearing in less than half the original sets, even if some of them are in fact representations of the set containing all elements.

    Reply

  10. Pingback: Amazing: Justin Gilmer gave a constant lower bound for the union-closed sets conjecture | Combinatorics and more

Leave a comment