A comparison between the Google estimator U for the fidelity and two improved estimators that we studied MLE (maximum likelihood estimator) and V (a variant of U). (More figures at the end of the post.)
Here are some links on quantum matters. I hope to return to them in more detail in some future posts.
1. A paper with Yosi Rinott and Tomer Shoham on the Statistics of Google’s experiment
Yosef Rinott, Tomer Shoham and Gil Kalai: Statistical aspects of the quantum supremacy demonstration, (arXive)
Abstract:
The notable claim of quantum supremacy presented by Google’s team in 2019 consists of demonstrating the ability of a quantum circuit to generate, albeit with considerable noise, bitstrings from a distribution that is considered hard to simulate on classical computers. Verifying that the generated data is indeed from the claimed distribution and assessing the circuit’s noise level and its fidelity is a purely statistical undertaking.
The objective of this paper is to explain the relations between quantum computing and some of the statistical aspects involved in demonstrating quantum supremacy in terms that are accessible to statisticians, computer scientists, and mathematicians.
Starting with the statistical analysis in Google’s demonstration, which we explain, we study various estimators of the fidelity, and different approaches to testing the distributions generated by the quantum computer. We propose different noise models, and discuss their implications. A preliminary study of the Google data, focusing mostly on circuits of 12 and 14 qubits is discussed throughout the paper.
I am greatly enjoying working with Yosi and Tomer, and I hope to devote a special post to the very interesting statistics of the Google supremacy experiment.
2. My paper The Argument against Quantum Computers, the Quantum Laws of Nature, and Google’s Supremacy Claims
Here is how the paper concludes
Over the past four decades, the very idea of quantum computation has led to many advances in several areas of physics, engineering, computer science, and mathematics. I expect that the most important application will eventually be the understanding of the impossibility of quantum error-correction and quantum computation. Overall, the debate over quantum computing is a fascinating one, and I can see a clear silver lining: major advances in human ability to simulate quantum physics and quantum chemistry are expected to emerge if quantum computational supremacy can be demonstrated and quantum computers can be built, but also if quantum computational supremacy cannot be demonstrated and quantum computers cannot be built.
Some of the insights and methods characteristic of the area of quantum computation might be useful for classical computation of realistic quantum systems – which is, apparently, what nature does.
The link above is the most recent version that will be updated; Here is the arXive version. A discussion on Hacker News.
3. My Dec 2019 surprise lecture and the panel discussion
My Dec 19 2019 (B.C.) surprise lecture at the mathematics of quantum computing school and the afternoon panel on the same day. It turned out that the lecture was videotaped. The slides can be seen in this post. Remarkably, social distancing was pioneered by the session chair toward the end of the lecture (while not justified in that case).
Here once again again is the link for the panel discussion on quantum supremacy of the same day (reviewed here) . Here is a quote of mine from the panel.
Of course, it is important to think what are the implications of quantum supremacy, is it useful? what does it say on the extended Church-Turing thesis? on prospects for quantum error-correction and universal quantum computers? etc. but I think that in the next few years one thing that we need to also concentrate on is the following question: Is the Google experiment correct? Is this a correct scientific verification of quantum supremacy?
4. My July 15 USTLC lecture
Four slides from my USTLC zoom lecture. (Click to enlarge.)
Here is the videotaped Zoom presentation and here are the slides.
5. A small taste of quantum poetry for the skeptics. (A full post is coming.)
Poems by Peter Shor and Renan Gross (click to enlarge)
Peter Shor pioneered quantum poetry for the skeptics over Twitter. There were many very nice contributions all over social media by Renan Gross, John Dowling, Vidit Nanda, ⟨dl|yonge|mallo⟩, Alfred Marcel Bruckstein, Kenneth Regan, and others. Keep the quantum poems coming! Of course, the poems should be taken with humor. Here is a small taste.
My short response to Peter’s poem
Understanding nature and ourselves is a worthy dream
Requiring no interaction with the supreme
Limericks
Jon Dowling
A quantum computer from Google,
Turned the Church-Turing thesis to strudel.
And yet there remain,
Many doubting this claim,
And we lash all of them with wet noodles.
Avi Wigderson
“There once was a quantum computer
Whose pet was a five-legged hamster …”
So Peter and Gil
Their grandchildren will
Tell “…happy they lived ever after”
Avi suggests a kids’ chorus saying “yeah, right” or “sure, sure”, after each line
Six-word stories
Ehud Friedgut
For sale: quantum computer. Never used.
Another 6-word story (mine) with a rhyme (of some sort)
Michelson and Morley weren’t Google employees.
6. More figures from my paper with Yosi and Tomer.
Various estimators for the fidelity for the Google data compared to simulations.
The model expected values compared to the empirical distribution. On the left for the real data and on the right for simulated data. As it turned out the Google noise model does not fit for the sample data. (Our readout model provides only a small improvement.)
The size biased distribution fits the model very well.
Combinatorics and more 
One interesting finding (from the conclusion) is: “Preliminary study of the Google data on 12 and 14 qubits suggests that neither Google’s basic noise model nor our refined readout errors model fit the observed data.”
Pingback: To cheer you up in difficult times 10: Noam Elkies’ Piano Improvisations and more | Combinatorics and more
Dear Gil Kalai,
Sorry if this is a naive question, but since in your recent paper with Yosi Rinott and Tomer Shoam you show that the Google noise model does not fit the observed data at all, not even approximately (Figure 8), does this mean Google accidentally vindicated you?
It seems that what you predicted would happen when the 10-30 qubit range is reached (more than Google’s earlier 9 qubit experiment) did in fact happen. While we retain some correlation to the desired distribution, perhaps due to the low term Fourier coefficients, the behavior becomes chaotic. Relatedly, did the Google team upload enough files to check the robustness of the experiment?
If I recall correctly, in your 2018 ICM paper you mention that such a disagreement with the model would be a strong support for your argument. Indeed, as you pointed out Martinis and Aaronson said that they expected QEC to work eventually precisely because they thought Google’s data fitted their model.
If the Google noise model does not fit the data, does that not cast doubt on their entire extrapolation argument? For example, let us assume we are sampling from the distribution
where 
is the uniform distribution and 
the desired exact distribution. Now let us apply a noise operator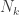 
to 
and get a distribution 
with added variance in the probabilities but keeping the total distance to the uniform distribution constant: 
where 
is a parameter, 
, and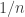 
is simply the probability of any observation under the uniform distribution. In effect, this adds variance by either moving a little towards or away from the uniform distribution, but we enforce 
so the total L1 distance to the uniform distribution remains the same for 
and 
. This is not unlike the amplitude amplification in Grover’s algorithm (if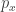 
was always 1). Now according to the 
model, if I estimate the fidelity 
through Maximum Likelihood for 
, the estimate would remain the same as for 
, but any assumption I make about the individual probabilities would not stand.
Unless I made a mistake somewhere above, by increasing
we would have a decaying correlation with the desired distribution but the same fidelity ? This is not an attempt to model the Google data (I am nowhere near knowledgeable enough in quantum computing to do that) but merely a thought experiment. Still, I think it is worth investigating which noise operators will result in similar fidelities but still don’t fit the model. I expect any that preserve the total L1 distance with the uniform distribution will have that property.
It is interesting that the readout error model provides only a small improvement. Readout errors (~3\%) are the highest contributor to Google’s error model but better accounting for them only marginally improves the fitting, suggesting there is indeed a new error mechanism, such as the error propagation you suggested. It seems to me Google used precisely the classical Preskill model of depolarizing noise, and that model does not fit the result. While Preskill showed that limited correlations (2012) could still enable QEC, at first glance it seems the model disagrees too much with the data? This brings to mind the position of Robert Alicki who also thinks the noise models are unrealistic. After your quantum debate with Aram back in 2012, he explained that FTQC arises when the noise models are too classical (exponentially decaying correlations, unbounded noise). He recently pointed out (arxiv:2001.00791) that error rates are improving much more slowly and that quantum open systems are more chaotic than commonly assumed, which I assume are two points in favor of your argument.
Sorry for the long rant, and I sincerely apologize if I made any mistakes here.
TL;DR : The Google (consensus) noise model does not fit at all the real data. Is it a strong signal that you were right all along?
Dear Quentin,
Thanks for your thoughtful comment. To your questions
1) you show that the Google noise model does not fit the observed data at all, not even approximately (Figure 8), does this mean Google accidentally vindicated you?
The mere fact that the data does not fit the basic noise model that Google offered does not by itself give support to my conjectures from the 2018 ICM paper. It might be the case that there is simply a better noise model. As you mentioned, we studied one such model in the paper, the readout error model. (In this model there is indeed an exponential decay of the Fourier coefficients.) But our readout model (and several variants) gave only a small improvement.
2) While we retain some correlation to the desired distribution, perhaps due to the low term Fourier coefficients, the behavior becomes chaotic.
We have some preliminary evidence that already in the Google 12 qubit experiment indeed the noisy distribution is chaotic (in other words, non-stationary) which is in agreement with the conjectures of my ICM 2018 paper. This happening already for 12 qubits is not a good sign.
3) “Relatedly, did the Google team upload enough files to check the robustness of the experiment?”
There are certainly plenty of files that we can study. Indeed we hopeג to see (and still hope) for more experiments in the classically tractable regime and, in particular, a) longer samples for 14-30 qubits, b) several samples of the same circuit. (We also hoped for c) samples for the 40-52 qubit regime.)
While b) is really what is needed to study robustness, what we did instead was to compare the first half and second half of the 0.5M samples.
4) “If the Google noise model does not fit the data, does that not cast doubt on their entire extrapolation argument?”
The Google argument in general and the fidelity estimator in particular do not rely on the specific model of noise that Google offered, this is mentioned in the Google paper and studied also by us. Still the fact that the Google model does not fit the data is not a good sign. You may further ask if evidence for chaotic (non-stationary) noisy distributions cast doubt on the extrapolation argument and this is indeed something I myself was puzzled about. (See the section “your argument, Gil” in https://gilkalai.wordpress.com/2019/11/13/gils-collegial-quantum-supremacy-skepticism-faq/ .) Formally, since all the statements are on the behaviour of a certain estimator F_XEB, then even a chaotic samples may demonstrate quantum supremacy, but practically this is not something one expects.
Thanks for the references to Aram’s new paper. There are various distinct issues related to correlation. One thing we are curious about is the correlation for readout errors. It seems that Google has valuable data (that we don’t have) that could be useful to study this matter and we suggested to them the possibility of exploring it together.
Thank you for your answers ! About the extrapolation, sorry for not being clear. My point was that there is indeed a variety of noise models that would result in the same fidelity in the Google experiment (same L1 distance with the uniform distribution) but still make a quantum computer incapable of QEC and thus of quantum supremacy in the strongest sense (ie. on useful problems). Perhaps this is a exception where a chaotic sample can demonstrate supremacy, but only a very narrow not-externally-useful problem? If I recall correctly, on your blog Peter Shor explained that the extrapolation argument would be valid only on mixing random circuits, perhaps this randomness is an edge case where, to put it bluntly, the variance does not matter and we care only about the mean of the distribution? Sorry if this is a naive question.
The fact that the preliminary evidence suggests that the distribution is indeed chaotic – as you said it would – is very interesting. Certainly since $label 2^{12} = 4096$ we would expect 0.5M samples to be enough for a reasonably good characterization of the noisy distribution. Having one half of the samples disagree with the other is not a good sign, that is likely generalizable since Google’s superconducting qubits are considered the most promising QC avenue. In my limited understanding, although these insights suggest quantum supremacy in the strongest sense is most probably out of reach, let us see the silver lining: we will have learned a lot about modeling noisy quantum systems. I am looking forward to reading your next paper!
Pingback: The Argument Against Quantum Computers – A Very Short Introduction | Combinatorics and more