A carpet of flowers in Shokeda, near Gaza, a few years ago.
This is the fourth post of this type (I (2008); II(2011); III(2015).) I started planning this post in 2019 but as it turned out, earlier drafts have quickly became obsolete and the process of writing this post did not converge.
Updates
Current academic life around here
In an earlier post I wrote about the hectic academic scene around here last spring. These were post-corona times, we had many visitors, workshops, conferences, and other activities. Since October 7, things are different also on the academic side of my life: only few visitors have come to Israel and I find myself talking much more than before with Israeli colleagues about a variety of academic matters and I also try to make progress on some old projects. A special personal goal is to transfer people who are mentioned on my homepage as “frequent collaborators” to the status of “coauthors”.
Jerusalem and Tel Aviv, HUJI and RUNI
Five years ago we sold our apartment in Jerusalem and bought and renovated an apartment in Tel Aviv in a neighborhood called “Kohav hatzafon” (The star of the north). Our apartment is very close to the Yarkon river and quite close to the beach. It is also rather close to where our three children and three grandchildren live.

The view from my home
As of October 2018 I am a Professor Emeritus at the Hebrew University of Jerusalem and I am a (half-time) Professor of Computer Science at the Reichman University (RUNI), formally known as the Herzelia Interdisciplinary Center (IDC). Essentially I split my activity between HUJI and RUNI. The Hebrew University and the area of mathematics are still homes for me, and I enjoy also my new hat as an RUNI-IDC faculty member in the very lovely Effi Arazi Computer Science school at Reichman University.

A beautiful group photo, the Efi Arazi School of Computer Science
This is not the first time I am a member of a computer science department. In 1990/1991 I visited the (CS) theory group at IBM, Almaden. I had the repeated thought that if only I could learn C++ and master it I will be able to make important contributions in practical aspects of computation! Logically, I was correct, since I did not learn C++. (Since then I reach a stage that I can slightly modify programs written by others in C++ and Python.) Next, I was affiliated for 5 years with the CS department at Yale (like Laci Lovasz and Ravi Kannan) before moving to Mathematics at Yale.
NYC visit fall 2022.
This was the first time since 1991 that we spent a prolonged period together abroad. Spending a semester at NYC was a long-time dream for Mazi and me and we had a great time. We are deeply thankful to the one and only Oded Regev who wonderfully hosted me at the Courant Institute. We also used this opportunity to make short visits to Chicago, Washington DC, Princeton, Rutgers, and Warren NJ.
A project with Dor, Noam and Tammy
Dor Minzer was visiting me during fall 2023 and Dor, Noam Lifshitz, Tamar Ziegler and me had a very nice project leading to the paper A dense model theorem for the Boolean slice. (And we have another project in progress.)
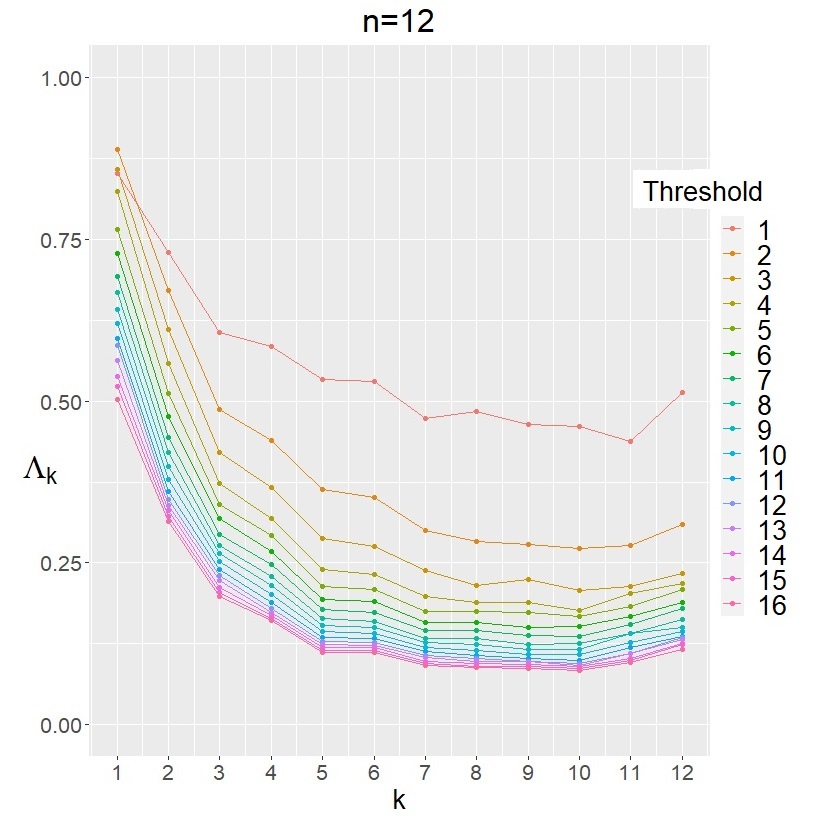
In our paper “we show that for every 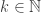 , the normalized indicator function of the middle slice of the Boolean hypercube $latex {0,1}^{2n}$ is close in Gowers norm to the normalized indicator function of the union of all slices with weight $latex t=n(mod2^{k−1})$. Using our techniques we also give a more general `low degree test’ and a biased rank theorem for the slice.” (A quote from the abstract.) As we recently learned, the case of linearity testing was proved independently by our friends Irit Dinur and Avishay Tal.
, the normalized indicator function of the middle slice of the Boolean hypercube $latex {0,1}^{2n}$ is close in Gowers norm to the normalized indicator function of the union of all slices with weight $latex t=n(mod2^{k−1})$. Using our techniques we also give a more general `low degree test’ and a biased rank theorem for the slice.” (A quote from the abstract.) As we recently learned, the case of linearity testing was proved independently by our friends Irit Dinur and Avishay Tal.

The following picture shows an analogy between integers and the Boolean cube, between primes and the middle slice of the Boolean cube, and between the papers I mentioned and two famous papers of early 2000.

A project with Micha, Moshe and Moria
Moria Sigron, Moshe White, Micha A. Perles and I are involved in a project of studying fine notions of order types (see this post and this lecture). Our purpose is to define and study a finer notion of order type for configurations of  points in $ latex \mathbb R^d$. This project is strongly motivated and influenced by the paper of Perles and Sigron “Strong general position” and by Barany’s recent paper on Tverberg’s theorem. Our fine order type relates to Tverberg’s theorem and strong general position, much in the same way that the (regular) order type relates to Radon’s theorem and general position.
points in $ latex \mathbb R^d$. This project is strongly motivated and influenced by the paper of Perles and Sigron “Strong general position” and by Barany’s recent paper on Tverberg’s theorem. Our fine order type relates to Tverberg’s theorem and strong general position, much in the same way that the (regular) order type relates to Radon’s theorem and general position.

An Interview with Toufik Mansour
Toufik Mansour interviewed me for the interview section of the journal “Enumerative Combinatorics and Applications” that Toufik founded..
Toufik: You have been managing a wonderful blog, “Combinatorics and more”, since 2008 and publish very interesting notes there. What was your motivation for it?
Me: Thank you! I think a main motivation was that I like to write about works of other people. I was also encouraged by several people that are mentioned in the “about” page, and wanted to experience collective mathematical discussions.
In a sense it is Aesop’s litigious cat fable in reverse. In Aesop’s story, a monkey helps two cats divide a piece of cheese by repeatedly eating from the larger piece. In my case, I think that I need to balance my blog and to do justice to areas/problems/people I have not mentioned yet, and the more I write the more I feel that work is still required to make the blog’s coverage (within subareas of combinatorics that I have some familiarity with) sufficiently complete, just, and balanced.
A potential new direction
Click here
Non-academic life around here
After January 2023 and before the war I tried to get involved in detailed dialogues with people with different views and especially with people who hold opposite views to mine about the political situation and the controversial judicial reforms. I have a personal preference for technical discussions over exchange of ribbing but it is not easy to find partners for calm detailed discussions.
Israel Journal of Mathematics: Nati’s birthday volume
Volume 256 of the Israel Journal of Mathematics is dedicated to Nati Linial on the occasion of his 70th birthday. Great papers, great personal dedications, and its all open access (Issue 1, Issue2). Rom Pinchasi’s paper deals with the odd area of the unit discs: Consider a configuration  of odd number of unit discs in the plane. The odd area
of odd number of unit discs in the plane. The odd area 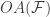 of the configuration is the area of all the points that are covered by an odd number of discs. The odd area conjecture asserts that
of the configuration is the area of all the points that are covered by an odd number of discs. The odd area conjecture asserts that
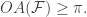
Some mathematical news
Traditionally, I start with some mathematical news. Indeed I had quite a list, but as this post did not progress, over the years, all the items found their way to regular posts in my blog and sometimes in other blogs. New items arrived and here is a large yet incomplete list.
1) The Daisy conjecture was refuted: David Ellis, Maria-Romina Ivan, and Imre Leader, disproved the Daisy conjecture.
2) Toward the dying percolation conjecture: Gady Kozma and Shahaf Nitzan showed a derivation of the dying percolation conjecture from a proposed conjecture about percolation for general graphs.
3) First passage percolation: Barbara Dembin, Dor Elboim, and Ron Peled settled a problem raised by Itai Benjamini, Oded Schramm and me about first passage percolation. The paper is On the influence of edges in first-passage percolation on  , and the planar case was proved in an earlier paper of Barbara, Dor, and Ron.
, and the planar case was proved in an earlier paper of Barbara, Dor, and Ron.
4) Around the Borsuk problem: Gyivan Lopez-Campos, Deborah Oliveros, Jorge L. Ramírez Alfonsín wrote about Borsuk’s problem in space and Reuleaux polyhedra. (On the arXiv there are quite a few interesting papers on Releaux polyhedra, Ball polyhedra and Meissner polyhedra.) Andrei M. Raigorodskii and Arsenii Sagdeev wrote a note on Borsuk’s problem in Minkowski spaces.
5) Around the flag conjecture and  conjecture: Dmitry Faifman, Constantin Vernicos, and Cormac Walsh proposed an interesting conjecture that interpolates between Mahler’s conjecture and my flag conjecture. There are several interesting papers about the
conjecture: Dmitry Faifman, Constantin Vernicos, and Cormac Walsh proposed an interesting conjecture that interpolates between Mahler’s conjecture and my flag conjecture. There are several interesting papers about the  conjecture by Gregory R. Chambers and Elia Portnoy and by Raman Sanyal and Martin Winter. (We discussed the
conjecture by Gregory R. Chambers and Elia Portnoy and by Raman Sanyal and Martin Winter. (We discussed the  problem, the flag conjecture and the related Mahler conjecture in this post.)
problem, the flag conjecture and the related Mahler conjecture in this post.)
6) Around Helly’s theorem: Nati Linial told me about Nóra Frankl, Attila Jung, and István Tomon’s paper about a quantitative fractional Helly theorem; Minki Kim and Alan Lew gave Extensions of the Colorful Helly Theorem for d-collapsible and d-Leray complexes, which contain also an interesting Tverberg-type theorem. Natan Rubin made a dramatic progress on point selections and halving hyperplanes.
7) Around the Kelly-Meka breakthrough. We wrote about the Kelly-Meka bounds for Roth’s theorem in this post. Zander Kelley, Shachar Lovett, and Raghu Meka, applied some techniques from that paper for showing Explicit separations between randomized and deterministic Number-on-Forehead communication, and together with Amir Abboud and Nick Fischer, for New Graph Decompositions and Combinatorial Boolean Matrix Multiplication Algorithms. I heard a lecture of Shachar Lovett about these breakthroughs and some further hopes. Yuval Filmus, Hamed Hatami, Kaave Hosseini, and Esty Kelman gave A generalization of the Kelley–Meka theorem to binary systems of linear forms, and Thomas F. Bloom, and Olof Sisask gave An improvement to the Kelley-Meka bounds on three-term arithmetic progressions.
8) Spectral graph theory. Matthew Kwan and Yuval Wigderson proved that The inertia bound is far from tight (and I heard Yuval giving a beautiful lecture about it.)
9) Hypercontractivity and groups. Equiped with a whole array of global hypercontractivity inequalities (see this post and this one) problems in group theory and their representations are becoming targets. Here are four papers in this direction: David Ellis, Guy Kindler, Noam Lifshitz, Dor Minzer, Product Mixing in Compact Lie Groups; Nathan Keller, Noam Lifshitz, Ohad Sheinfeld, Improved covering results for conjugacy classes of symmetric groups via hypercontractivity; Peter Keevash, Noam Lifshitz, Sharp hypercontractivity for symmetric groups and its applications; Noam Lifshitz, Avichai Marmor Bounds for Characters of the Symmetric Group: A Hypercontractive Approach.
10) Hodge theory and combinatorics. Semyon Alesker told me about the paper of Andreas Bernig, Jan Kotrbatý, and Thomas Wannerer, Hard Lefschetz theorem and Hodge-Riemann relations for convex valuations. There are many interesting other developments on Hodge theory and combinatorics for metric, arithmetic, and combinatorial study of polytopes and convex sets.
11) AP with restricted difference and the theory of computing. Amey Bhangale, Subhash Khot, and Dor Minzer are involved in a long term project primarily addressing important problems in theoretic computer science with important applications to additive combinatorics. Here is one of their papers in the additive combinatorics direction: Effective Bounds for Restricted 3-Arithmetic Progressions in 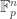 .
.
12) Thresholds. Following the Park-Pham proof of the expectation threshold conjecture (that I and Jeff Kahn reluctantly made), and the earlier Frankston-Kahn-Narayanan-Park proof of a weaker fractional version, there were quite a few subsequent papers in various directions and I will mention only few of them. Short proofs were offered by P. Tran, V. Vu and by Bryan Park and Jan Vondrák and (for more general product measures). Elchanan Mossel, Jonathan Niles-Weed, Nike Sun, and Ilias Zadik’s paper On the Second Kahn–Kalai Conjecture proves a weaker version of a second conjecture from our paper for graphs. (Both the main conjecture and the second conjecture looked at the time “too good to be true.” We had, however, stronger confidence in a third conjecture that would derive the second conjecture from the first. This third conjecture turned out to be false 🙂 .)
Ashwin Sah, Mehtaab Sawhney, and Michael Simkin found the Threshold for Steiner triple systems. Michael gave a talk at HUJI about this paper and explained to me also how the expectation threshold theorem can lead to exact results even in cases where the gap between the expectation threshold and the threshold is smaller than 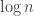 . Let me mention three more papers: Huy Tuan Pham, Ashwin Sah, Mehtaab Sawhney, and Michael Simkin wrote A Toolkit for Robust Thresholds; Searching for (sharp) thresholds in random structures: where are we now? by Will Perkins, and Threshold phenomena for random discrete structures by Jinyoung Park.
. Let me mention three more papers: Huy Tuan Pham, Ashwin Sah, Mehtaab Sawhney, and Michael Simkin wrote A Toolkit for Robust Thresholds; Searching for (sharp) thresholds in random structures: where are we now? by Will Perkins, and Threshold phenomena for random discrete structures by Jinyoung Park.
In a different direction Eyal Lubetzky and Yuval Peled estimated The threshold for stacked triangulations. This paper is related to the Linial-Meshulam model for random simplicial complexes, to bootstrap percolation, and to algebraic shifting.
13) Achieving Shannon capacity. A proof that Reed-Muller codes achieve Shannon capacity on symmetric channels, by Emmanuel Abbe and Colin Sandon. In my previous “update and plans” I wrote about remarkable proofs (using sharp threshold results) that Reed-Muller Codes Achieve Capacity on Erasure Channels. The new paper by Emmanuel and Colin shows that this is also the case for symmetric channels. The proof uses a terrific combination of combinatorial and analytical tools and novel ideas that are of much interest on their own.
14) Envy free partitions. Amos Fiat and Michal Feldman told me about a great problem, but, on second thought, it fits very nicely with the “test your intuition” corner.
15) Reconstructing shellable spheres from their puzzles. Blind and Mani proved that simple polytopes are determined by their graphs. I gave a simple proof that applies (in the dual form) to a subclass of shellable spheres. (see this post). It is an open conjecture that simplicial spheres are determined by their “puzzle” (namely the incidence graph of facets and subfacets). The case of shellable spheres has now been proved by Yirong Yang in the paper Reconstructing a Shellable Sphere from its Facet-Ridge Graph.
16) Around the (generalized) Hardy-Littlewood conjecture and inverse Gowers theorem. A great mathematical achievement of the last decades was the proof by Ben Green, Terry Tao and Tamar Ziegler of the (generalized) Hardy-Littlewood conjecture on the asymptotic number of solutions to equations over the primes when the number of variables is larger than the number of equations by two or more. (Arithmetic progressions of length  is an important special case.) This theorem required a proof of the inverse theorem for Gowers norms. In recent years better and better quantitative versions of the inverse Gowers theorem were found by Manners, and recently James Leng, Ashwin Sah, and Mehtaab Sawhney gave almost polynomial bounds in Quasipolynomial bounds on the inverse theorem for the Gowers $latex U^{s+1}[N]$-norm. This paper is related to another paper by the same authors with improved bounds for Szemeredi’s theorem, and to an earlier paper by Leng Efficient Equidistribution of Nilsequences.
is an important special case.) This theorem required a proof of the inverse theorem for Gowers norms. In recent years better and better quantitative versions of the inverse Gowers theorem were found by Manners, and recently James Leng, Ashwin Sah, and Mehtaab Sawhney gave almost polynomial bounds in Quasipolynomial bounds on the inverse theorem for the Gowers $latex U^{s+1}[N]$-norm. This paper is related to another paper by the same authors with improved bounds for Szemeredi’s theorem, and to an earlier paper by Leng Efficient Equidistribution of Nilsequences.
Regarding additive combinatorics let me also mention three survey articles about the utility of looking at toy versions over finite fields of problems in additive combinatorics. In some cases you can transfer the methods from the finite field case to the integer case. For some methods this is not known. It is a lovely question if there are ways to transfer results from the finite field case to the case of integers. The survey article are by Ben Green from 2005, by Julia Wolf from 2015 and by Sarah Peluse from 2023.
17) Ramanujan graphs. Ryan O’Donnell and coauthors wrote several exciting papers about Ramanujan graphs. Explicit near-fully X-Ramanujan graphs by Ryan O’Donnell and Xinyu Wu; Explicit near-Ramanujan graphs of every degree, by Sidhanth Mohanty, Ryan O’Donnell, Pedro Paredes; and Ramanujan Graphs, by Sidhanth Mohanty and Ryan O’Donnell.
Plans
Traditionally I write here about my plans for the blog. I plan to tell you more over my blog about my own mathematical projects and papers and perhaps also about half-baked ideas. I plan to write, at last, something about cryptography, to explain Micha Sageev’s construction (as promised here), and to revisit a decade old MO question (related to a lot of interesting things).
My own research directions
Let me briefly share with you what I think about mathematically. One topic in my research is about analysis of Boolean (and other) functions, discrete Fourier analysis, sensitivity and stability of noise, and related matters. This study has applications within combinatorics and mathematics and also to theoretical computer science, social choice theory and to quantum computing which, in the last two decades, has become a central area of my interest. Another topic that I study is geometric, topological and algebraic combinatorics. I study especially convex polytopes and related cellular objects and Helly-type theorems. This topic is related to linear programming and other areas of theoretical computer science. Pursing mathematical fantasies of various kind (what Miklos Simonovits called “Sunday’s afternoon mathematics”) is also a favorite activity of mine, which is one reason I liked polymath projects while they lasted.
Programming
One of my personal plans is to learn (again, I learned FORTRAN in my teens) to program, and to actually program from time to time. Some of my mathematical friends who are fluent at programming like Sergiu Hart, Dan Romik, (and, of course, Doron Zielberger) do use programming in their research. (In the case of Doron, perhaps Shalosh B. Ekhad uses Doron for her research.) Another of my mathematical heroes, Boris Tsirelson, told me once that he liked programming a lot and it was never a clear call for him if he likes proving theorems and developing mathematical theories more than writing codes. I know that ChatGPT and alike can now program for me, and I think that this will make re-learning programming and actually using programming for research easier.
A planned Kazhdan’s seminar on hypercontractivity.
In 2003/2004 David Kazhdan and I ran a seminar on polytopes, toric varieties, and related combinatorics and algebra, and it was centered around a theorem of Kalle Karu. My plan was to have such a seminar every decade and the next one (with Leonid Polterovich, Dorit Aharonov, and Guy Kindler) was in 2019 about computation, quantumness, symplectic geometry, and information. (Life events caused it to be delayed by a few years.) I also participated also in Karim Adiprasito’s Kazhdan seminar on “positivity in combinatorics and beyond” where he presented his proof of the g-conjecture. We now have a plan to run a Kazhdan seminar in 2025/2026 on hypercontractivity together with Noam Lifshitz and Guy Kindler and perhaps others.


 Snapshots from Dorit’s lecture: The top-left slide is about the threshold theorem (mid-late 90s). The bottom-left slide is about later developments related to the threshold theorem (and the 2005 picture that I mentioned above); The top-right slide is about how a classical computer can test that a quantum computer did what it claimed to do. The 2008 paper of Aharonov, Ben-Or and Elad Eban started an exciting direction, and Dorit mentioned that it was motivated in part by Oded Goldreich and Madhu Sudan’s (skeptical) question about evidence for quantum physics in the high complexity regime. The bottom-right shows Dorit and Tal Rabin during the lecture. Below, Dorit’s question on the physics description of quantum fault tolerance and the transition from quantum to classical physics and her 1999 paper on the transition from the quantum world to the classic world.
Snapshots from Dorit’s lecture: The top-left slide is about the threshold theorem (mid-late 90s). The bottom-left slide is about later developments related to the threshold theorem (and the 2005 picture that I mentioned above); The top-right slide is about how a classical computer can test that a quantum computer did what it claimed to do. The 2008 paper of Aharonov, Ben-Or and Elad Eban started an exciting direction, and Dorit mentioned that it was motivated in part by Oded Goldreich and Madhu Sudan’s (skeptical) question about evidence for quantum physics in the high complexity regime. The bottom-right shows Dorit and Tal Rabin during the lecture. Below, Dorit’s question on the physics description of quantum fault tolerance and the transition from quantum to classical physics and her 1999 paper on the transition from the quantum world to the classic world.