A Nice Example Related to the Frankl Conjecture

Posted on November 30, 2022 by Gil Kalai

Updates: 1. Peter Frankl brought to my attention that the very same example appeared in a paper by Dynkin and Frankl “Extremal sets of subsets satisfying conditions induced by a graph“. 2. Sam Hopkins gave a lovely reference to Ravi Boppana’s note “A Useful Inequality for the Binary Entropy Function” where Ravi Boppana gives a simple proof of a key inequality that is at the heart of the recent progress on the union-closed sets conjecture. Ravi explains some interesting history on this inequality, and how he used it in a quite different context over 30 years ago.

The example

As a follow up to my previous post about Gilmer’s breakthrough regarding Frankl’s conjecture, here is a very nice example (from the paper of Zachary Chase and Shachar Lovett) related to the conjecture.

Let \psi=\frac {3-\sqrt 5}{2} = 0.38..

Consider the following families of subsets of [n]

{\cal F}_1=\{S \subset [n]: |S|=\psi n + n^{2/3}\}, and

{\cal F}_2 = \{ T \subset [n]: |T|>(1-\psi) n \}.

Now let {\cal F}={\cal F}_1 \cup {\cal F}_2.

Here are some observations:

  1. |{\cal F}_2| = o(|{\cal F}_1|).
  2. The number of pairs (S,T):S,T \in {\cal F} whose union is also in {\cal F} is (1-o(1)) {|\cal F}|^2.
  3. For every \epsilon >0, as n grows, no element k \in [n] belongs to more than (\psi+\epsilon) |{\cal F}| sets in {\cal F}.

The first assertion holds because {{n} \choose {\psi n +n^{2/3}}} is exponentially larger (in a fractional power of n) than {{n} \choose {(1-\psi )n}}.

For the second assertion we need to show that a typical union of a pair of sets in {\cal F}_1 belongs to {\cal F}_2. Note that the intersection of two random subsets of [n] of size \phi n is \phi ^2 n and hence their union is of size 2\phi - \phi^2. As it happens the solution of the equation 2\phi-\phi^2 = 1-\phi is precisely our \psi=\frac {3+\sqrt 5}{2}. So letting \phi=\psi + n^{-1/3} we get that a typical union of two sets from {\cal F}_1 is in {\cal F}_2.

The third assertion follows from the fact that an element k \in [n] belongs to a fraction of \psi + n^{-1/3}  sets in {\cal F}_1.

This shows that a natural stability version of Frankl’s conjecture is incorrect, and gives some hint on the appearance of the parameter \psi.

Stability result

Such a stability version is correct when we replace 1/2 with \psi. Chase and Lovett improved Gilmer’s method and  proved that

Theorem: If  \cal F is a (1-\epsilon)-approximate union closed set system, where \epsilon <1/2, then there is an element which is contained in a (\psi-\delta) fraction of sets in \cal F, where

\delta=2\epsilon (1+\frac {\log (1/\epsilon)}{\log |{\cal F}|}).

An invitation for further discussion

I will be happy to see, based on Gilmer’s paper and the five follow-up papers, a detailed, as simple as possible, explanation of Frankl’s conjecture for the parameter \psi, to learn what is involved in Sawin’s improvement that goes beyond \psi, and to understand the counterexamples for Gilmer’s proposal towards the full conjecture, as well as thoughts, ideas and remarks of various kind on the problem.

Links to the papers

  1. Justin Gilmer, A constant lower bound for the union-closed sets conjecture
  2. Will Sawin, An improved lower bound for the union-closed set conjecture
  3.  Zachary Chase, Shachar Lovett, Approximate union closed conjecture
  4. Ryan Alweiss, Brice Huang, Mark Sellke, Improved Lower Bound for the Union-Closed Sets Conjecture 
  5. David Ellis, Note: a counterexample to a conjecture of Gilmer which would imply the union-closed conjecture
  6. Luke Pebody, Extension of a Method of Gilmer
  7. (Dec 9.) Lei Yu, Dimension-Free Bounds for the Union-Closed Sets Conjecture 

This entry was posted in Combinatorics, Open discussion, Open problems and tagged , , , , , , , , , , . Bookmark the permalink.

7 Responses to A Nice Example Related to the Frankl Conjecture

  1. Pingback: Progress on the union-closed sets conjecture – SPP 2026

  2. Jon Awbrey says:
    November 30, 2022 at 3:40 pm

    Re: thoughts, ideas and remarks of various kind on the problem.

    I can’t say I really have a solid sense of the problem yet but the last time it came up in these parts I was following a clue from Lipton & Regan toward what I saw as a differential approach. I didn’t get very far at the time but here’s a first link for what it’s worth.

    Frankl, My Dear …

    Reply
  3. Imre Polik says:
    November 30, 2022 at 4:50 pm

    Looks like the definition of psi is wrong.

    GK: Thanks, Imre; corrected.

    Reply
  4. Gil Kalai says:
    December 1, 2022 at 11:13 am

    The example shows that the conclusion of Frankl’s conjecture does not approximately hold for approximately union-closed families in the sense that for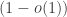 (1-o(1)) of pairs of sets in the family the union is also in the family.

    It is still possible the conclusion of Frankl’s conjecture does approximately hold for approximately union-closed families in the sense that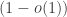 (1-o(1)) of sets that are unions of sets in the family, belong to the family.

    Reply
    • Ilan K says:
      December 5, 2022 at 6:27 pm

      Indeed. If we would try to tweak Chase and Lovett’s example to this stricter approdximately union-closed definition, we would run into problems. From results about largest k-uniform families L-avoiding (the symmetric distance between any pair is not in some subset of forbidden distances L), we would only be able to take a very small fraction of the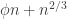 \phi n + n^{2/3} layer, if we would want to satisfy the stricter definition.

      This leads me to wonder: can we find some upper bound on

      H(\mathbb{F\cup F}) / H(\mathbb{F}),

      for a union-closed family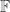 \mathbb{F}, so that each element appears in at most 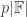p|\mathbb{F}| sets.

      Reply

  5. Pingback: The Gift of Nonconstructivity | Gödel's Lost Letter and P=NP

  6. Sam Hopkins says:
    January 30, 2023 at 5:19 am

    You might also be interested in this note “A Useful Inequality for the Binary Entropy Function” by Ravi Boppana where he gives a simple proof of a key inequality that is at the heart of the recent progress on the union-closed sets conjecture: https://arxiv.org/abs/2301.09664. Actually he explains some interesting history on this inequality, how he used it in a quite different context over 30 years ago.

    Reply

Leave a comment