To cheer you up in difficult times 34: Ringel Circle Problem solved by James Davies, Chaya Keller, Linda Kleist, Shakhar Smorodinsky, and Bartosz Walczak

Gerhard Ringel considered in 1959 the following:

Consider a finite family of circles such that every point in the plane is included in at most two circles. What is the minimum number of colors needed to color the circles so that tangent circles are colored with different colors?

Ringel 1959 circle problem is the question if this minimum number of colors is bounded.

I mentioned the problem in a post about eight coloring problems for arrangements of circles and pseudocircles, three years ago. (For another recently solved conjecture by Ringel see this post.)

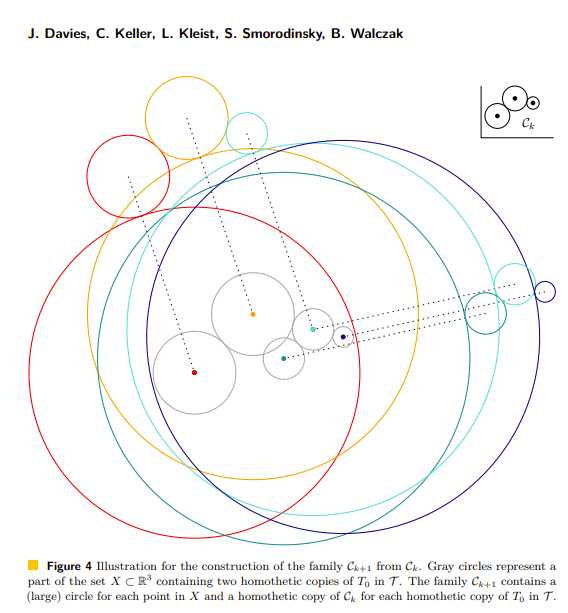
In a recent arXiv paper James Davies, Chaya Keller, Linda Kleist, Shakhar Smorodinsky, and Bartosz Walczak solved the problem and showed that any finite number of colors does not suffices. In fact the proved considerably more. The paper is

A solution to Ringel circle problem,

and here is the abstract

Abstract: We construct families of circles in the plane such that their tangency graphs have arbitrarily large girth and chromatic number. This provides a strong negative answer to Ringel’s circle problem (1959). The proof relies on a (multidimensional) version of Gallai’s theorem with polynomial constraints, which we derive from the Hales-Jewett theorem and which may be of independent interest.

Congratulations to the authors.