Coloring Problems for Arrangements of Circles (and Pseudocircles)

To supplement and celebrate Aubrey de Grey’s result here are

Eight problems on coloring circles

A) Consider a finite family of unit circles. What is the minimum number of colors needed to color the circles so that tangent circles are colored with different colors?

This is the question about the chromatic number of the plane. (Or the maximum chromatic number of planar unit-distance graphs.) By the Aubrey de Grey’s result the answer is 5, 6, or 7.

B) Consider a finite family of non-overlapping unit circles. What is the minimum number of colors needed to color the circles so that tangent circles are colored with different colors?

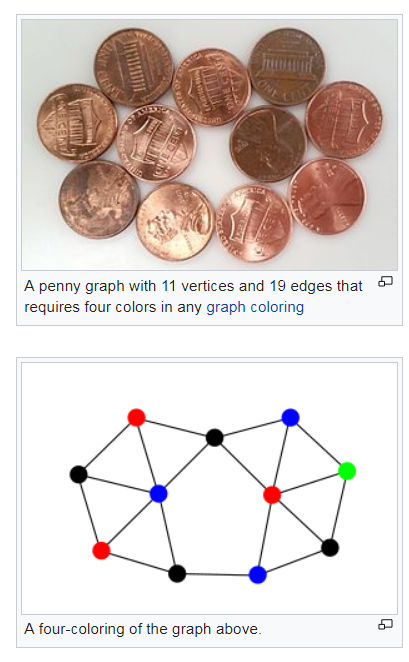
Now we talk about planar unit-distance graphs where the distance between every pair of points is at least one. Those are also called Penny graphs. The answer is four.

C) Consider a finite family of pairwise intersecting unit circles. What is the minimum number of colors needed to color the circles so that tangent circles are colored with different colors?

This is a the (finite) planar Borsuk problem. (Now we talk about planar unit-distance graphs where the distance between every pair of points is at most one.) The answer is 3, and this follows from a simple characterization these graphs.

D) Consider a finite family of non-overlapping circles. What is the minimum number of colors needed to color the circles so that tangent circles are colored with different colors?

By Koebe’s circle packing theorem (see this recent post) this is precisely the four color theorem so the answer is 4.

E) Consider a finite family of  circles. What is the minimum number of colors needed to color the circles so that tangent circles are colored with different colors?

Unless we make some further assumption the answer is infinite. Rom Pinchasi proved that collors suffice and also  gave an example of circles where the chromatic number is at least .

F) Consider a finite family of  circles such that every point in the plane is included in at most two circles.  What is the minimum number of colors needed to color the circles so that tangent circles are colored with different colors?

Ringel’s circle conjecture (see this paper by Jackson and Ringel) asserts that the number of colors is bounded. (There is an example that five colors are required.)

G) Consider a finite family of pairwise intersecting circles. What is the minimum number of colors needed to color the circles so that tangent circles are colored with different colors?

H) Consider a finite family of  pseudocircles.  Here every pseudocircle is a closed simple path and two pseudocicles are either disjoint or hace two crossing points. Two pseudocircles are adjacent if the lens described by them does not contain any point from any other pseudocircle. What is the minimum number of colors needed to color the pseudocircles so that adjacent pseudocircles are colored with different colors? (In particular, is this number finite?)

Remarks

Number of edges and other properties

Each of the above questions give rise to a family of graphs and lead to other interesting questions about these graphs. For example, we can ask what is the maximal number of edges in each case.

For unit distance graphs (question A) this is the famous  Erdős unit distance problem. (Here is a survey by Szemeredi).

The Maximum number of edges of Borsuk planar graphs (question C) is (see this proof using lice), and this immediately implies that their chromatic number is at most three.

The maximum number of edges of Penny graphs (question B) is known and there is an intruiging conjecture for triangle free Penny graphs.

The maximum number of edges of (simple) planar graphs (question D) as follows easily from Euler’s theorem.

Alon, Last, Pinchasi, and Sharir  showed an upper bound of for the number of edges in the tangent graph for pairwise intersecting circles. (Question G.)

An intruiging conjecture by Pinchasi, Sharir, and others is that planar tangent graphs (Question E) with vertices can have at most edges. This conjecture proposes a profound extension of the Szemeredi–Trotter theorem. The best known upper bound is by Marcus and Tardos.

Sylvester-Gallai type results

For circles that pairwise intersect, Rom Pinchasi proved a Gallai–Sylvester conjecture by Bezdek asserting that (for more than 5 circles) there is always a circle tangential to at most two other circles. This was the starting point of important studies  concerning arrangement of circles and pseudo-circles in the plane.

High dimensions

Each of the above questions extends to higher dimensions and also here they include some well known problems. It is a famous result by Frankl and Wilson that the cromatic number of is exponential in . We now know (see this post) that there are -dimensional “hyper-penny” graphs with minimal degree that is exponential in . Is the chromatic number of such graphs can also be exponential in ?

When you ask these questions without stress. (Adding the strong Arnold property).

A stress (affine stress to be precise) of a geometric graph is an assignement of weights to edges so that every vertex is in equilibrium. We can ask many of the problems above (e.g. see this post) when we assume that the graph is stress-free, namely does not admit non-trivial stresses. (When we consider circles of different sizes we probably need to consider stresses in three dimensions.) We can think about stress-freeness as saying that we have a “non coincidental” configuration.