Ringel’s conjecture solved (for sufficiently large n)
A couple weeks ago and a few days after I heard an excellent lecture about it by Alexey Pokrovskiy in Oberwolfach, the paper A proof of Ringel’s Conjecture by Richard Montgomery, Alexey Pokrovskiy, and Benny Sudakov was arXived. Congratulations to Richard, Alexey, and Benny!
Here is the abstract:
A typical decomposition question asks whether the edges of some graph G can be partitioned into disjoint copies of another graph H. One of the oldest and best known conjectures in this area, posed by Ringel in 1963, concerns the decomposition of complete graphs into edge-disjoint copies of a tree. It says that any tree with n edges packs 2n+1 times into the complete graph
. In this paper, we prove this conjecture for large n.
Previous posts: Test your intuition 43 – What will be the distribution of anabraists and algasisits; MIP*=RE. For Ringel’s circle conjecture, see this post.
Absorption and distributive absorption
First the authors construct approximate decomposition (they divide the problem into two cases) and then they apply a powerful method called absorption. Here is what they write:
To prove our finishing lemmas, we use an absorption strategy. Absorption has its origins in work by Erdős, Gyárfás and Pyber [5] and Krivelevich [14], but was codified by Rödl, Ruciński and Szemerédi [20] as a versatile technique for extending approximate results into exact ones. For both Case A and Case B we use a new implementation of distributive absorption, a method introduced by the first author in [16].
Absorption is one of the most powerful current methods in extremal combinatorics. It is important in the construction of designs (See here, here, here, and here, and my own survey), and in the the solution of several other important conjectures.
Here are links to the pioneering papers mentioned above.
P. Erdős, A. Gyárfás and L. Pyber [5] Vertex coverings by monochromatic cycles and trees. Journal of Combinatorial Theory, Series B, 90–95, 1991.
M. Krivelevich [14] Triangle factors in random graphs. Combinatorics, Probability and Computing, 6: 337–347, 1997.
V. Rödl, A. Ruciński and E. Szemerédi [20] A dirac-type theorem for 3-uniform hypergraphs. Combin. Probab. Comput., 15:229–251, 2006.
And Montgomery’s paper on distributive absorption:
R. Montgomery [16] Spanning trees in random graphs, Advances in Mathematics, 2019
A related paper with an amusing name and an amusing abstract is: E. Szemerédi “Is laziness paying off? (`Absorbing’ method).” The abstract of the paper reads “We are going to mention some embedding problems. The main ideas of most of the solution of these problems are that do not work too much. Finish the job almost, then use some kind of absorbing configuration (that is what we call laziness).”
Montgomery, Pokrovskiy, and Sudakov’s paper concludes with two related famous conjectures:
The graceful tree conjecture
Motivated by Ringel’s conjecture, in 1967 Alexander Rosa conjectured that every tree T with n edges admits a graceful labeling, namely a labeling of the vertices by the numbers 0,1,…,n such that if we label an edge by the absolute value of the difference of the labels for its two vertices, then all the edge labels are different!
This famous conjecture (stronger than Ringel’s conjecture) is known as the Graceful Tree conjecture and also as the Ringel-Rosa-Kötzig conjecture. It is still open.
Packing trees of different sizes: Gyárfás conjecture
Gyárfás conjecture (1976): Let be trees with
having
vertices for each
. Then the edges of
can be decomposed into
trees which are isomorphic to
respectively.


Wow, incredible. Thanks for sharing. Ringel is one of my favourite conjectures but not living in a math department any more I wouldn’t have known about this sensational news if it wasn’t for your blog!
I’m sorry, I had trouble actually figuring what absorbing actually is. I read through the paper by Erdos. Which idea in there actually uses absorption? Thanks.
In the proof of Theorem 1, they start by finding a red “triangle cycle” of length
of length  . This is a cycle
. This is a cycle  together with vertices
together with vertices 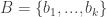 such that
such that 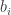 is adjacent to
is adjacent to 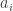 and
and  . The nice thing about a triangle cycle is that after removing any subset of
. The nice thing about a triangle cycle is that after removing any subset of  , it still has a Hamiltonian cycle. This triangle cycle will be the “absorber.”
, it still has a Hamiltonian cycle. This triangle cycle will be the “absorber.”
Next they apply Erdos-Gallai to greedily find monochromatic cycles until the number of uncovered vertices is significantly smaller than .
.
Finally, they apply Lemma 1 to the bipartite graph induced by the leftover vertices and the set from the triangle cycle. This ensures that all of the leftover vertices are covered with cycles (i.e. “absorbed”) and it didn’t matter which vertices from
from the triangle cycle. This ensures that all of the leftover vertices are covered with cycles (i.e. “absorbed”) and it didn’t matter which vertices from  were used because whatever remains of
were used because whatever remains of  can be covered by a single cycle.
can be covered by a single cycle.
Pingback: To cheer you up in difficult times 34: Ringel Circle Problem solved by James Davies, Chaya Keller, Linda Kleist, Shakhar Smorodinsky, and Bartosz Walczak | Combinatorics and more
Pingback: Greatest Hits 2015-2022, Part II | Combinatorics and more